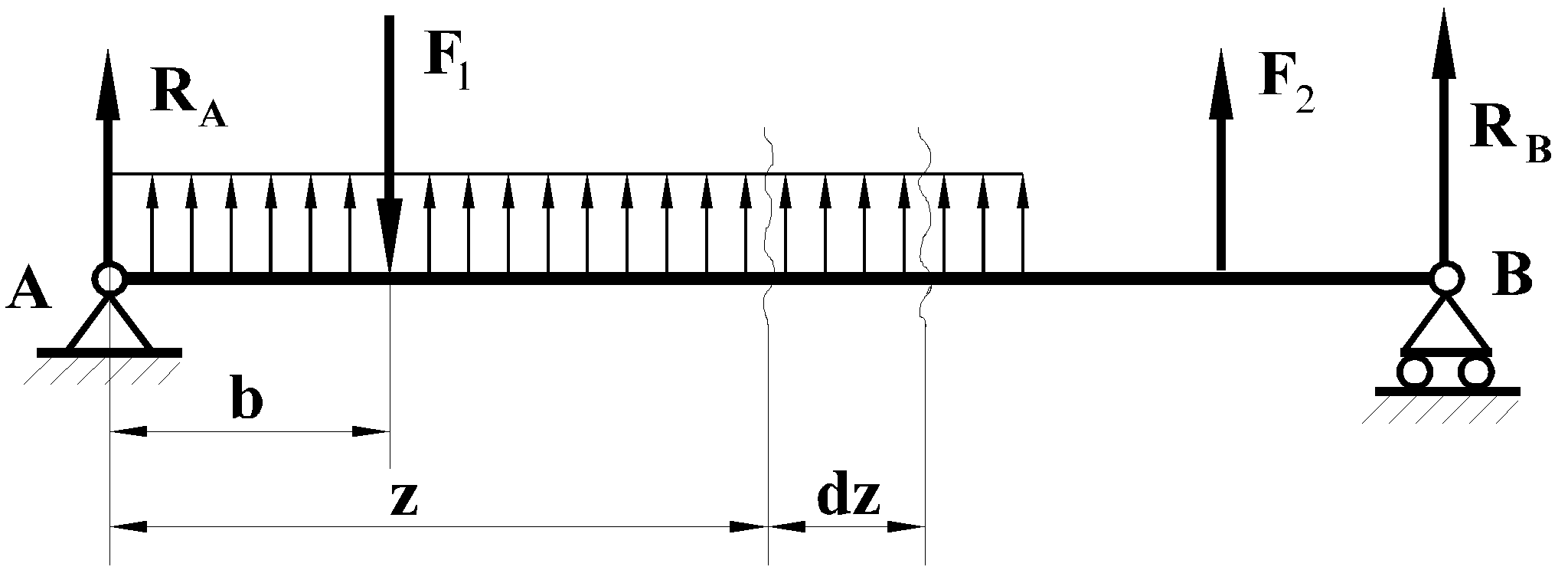
49. Связь между поперечной силой и изгибающим моментом.

Между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки легко установить определенную зависимость. Рассмотрим балку, нагруженную произвольной нагрузкой (рисунок 5.10). Определим поперечную силу в произвольном сечении, отстоящем от левой опоры на расстоянии Z. Проецируя на вертикаль силы, расположенные левее сечения, получаем  (5.1) Вычисляем поперечную силу в сечении, рас­положенном на расстоянии z + dz от левой опоры.  (5.2) Рисунок 5.8. Вычитая (5.1) из (5.2) получаем dQ = qdz, откуда то есть производная от поперечной силы по абсциссе сечения балки равна интенсивности распределенной нагрузки. Вычислим теперь изгибающий момент в сечении с абсциссой z, взяв сумму моментов сил, приложенных слева от сечения. Для этого распределенную нагрузку на участке длиной z заменяем ее равнодействующей, равной qz и приложенной в середине участка, на расстоянии z/2 от сечения:  (5.3)   (5.4) Вычитая (5.3) из (5.4), получаем приращение изгибающего момента Выражение в скобках представляет собой поперечную силу Q. Тогда  . Отсюда получаем формулу  (5.5) Таким образом, производная от изгибающего момента по абсциссе сечения балки равна поперечной силе (теорема Журавского).  Взяв производную от обеих частей равенства (5.5), получим т. е. вторая производная от изгибающего момента по абсциссе сечения балки равна интенсивности распределенной нагрузки. Полученные зависимости будем использовать при проверке правильности построения эпюр изгибающих моментов и поперечных сил. 

50 Способы построения эпюр Ми и q.

1. Виды опорных закреплений

С технической точки зрения опорные закрепления конструкций весьма разнообразны. Прирешении задач сопромата, все многообразие существующих опорных устройств схематизируется в виде ряда основных типов опор, из которых

наиболее часто встречаются: шарнирно-подвижная опора (возможные обозначения для нее представлены на рис.1,а), шарнирно-неподвижная опора (рис.1,б) и жесткое защемление, илизаделка (рис.1,в).

Рис. 1

 

В шарнирно-подвижной опоре возникает одна опорная реакция, перпендикулярная опорной плоскости. Такая опора лишает опорное сечение одной степени свободы, то есть препятствует смещению в направлении опорной плоскости, но допускает перемещение в перпендикулярном направлении и поворот опорного сечения. В шарнирно-неподвижной опоре возникают вертикальная и горизонтальная реакции. Здесь невозможны перемещения по направлениям опорных стержней, но допускается поворот опорного сечения. В жесткой заделке возникают вертикальная и горизонтальная реакции и опорный (реактивный) момент. При этом опорное сечение не может смещаться и поворачиваться.При расчете систем, содержащих жесткую заделку, возникающие опорные реакции можно не определять, выбирая при этом отсеченную часть так, чтобы заделка с неизвестными реакциями в нее не попадала. При расчете систем на шарнирных опорах реакции опор должны быть  определены обязательно. Уравнения  статики, используемые для этого, зависят от вида системы (балка, рама и др.) и будут приведены в соответствующих разделах настоящего пособия.