39. Закон Гука при растяжении и сжатии, коэффициент Пуассона.

Опыты показывают, что при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются. При сжатии наоборот.

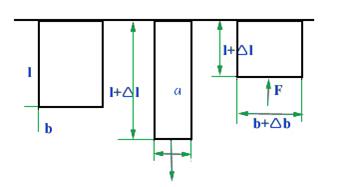
Рис.2.3

 (2)-относительное удлинение или линейные деформации.

Закон Гука гласит, что абсолютная продольная линейная деформация Д/ прямо пропорциональна продольной силе N, Длине стержня / и обратно пропорциональна жесткости при растяжении (сжатии) ЕА, Где Е — Модуль Юнга (модуль упруго­сти первого рода); А — площадь поперечного сечения стержня.

Абсолютная величина отношения относительной попереч­ной линейной деформации е, к относительной продольной ли­нейной деформации е называется коэффициентом Пуассона:

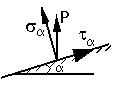
40. Напряжения в наклонных сечениях при сжатии и растяжении.

Напряжение наклонных сечений при растяжении-сжатии

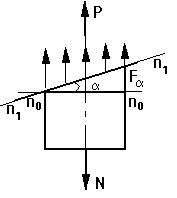
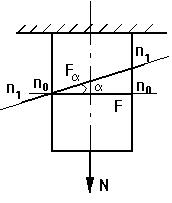
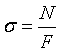
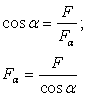
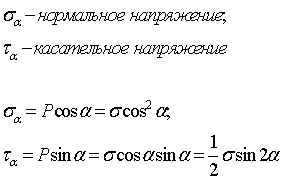
К 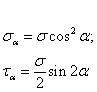асательное напряжение максимальное на площадках, наклоненных под углом в 450 к оси стержня;

sa - максимальные напряжения параллельные оси равны 0.

П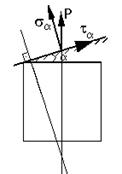 равило знаков.

а) Для нормальных напряжений: если направлено от сечения – положительно, если – к сечению – отрицательно.

б) Для касательных напряжение: если поворачивается относительно точки С, лежащей на внутренней нормали по часовой стрелке – отрицательно, против часовой стрелки – положительно.

41 Статически неопределимые задачи при растяжении и сжатии.

42. Силовые, температурные и монтажные задачи.

43 Сдвиг. Основные понятия.

Сдвиг- это вид деформации, при котором одна часть стержня смещается относительно другой (как скользят, например, карты в колоде). Деформация сдвига будет происходить, если к стержню приложить две равные по модулю противоположно направленные силы (P), перпендикулярные к его оси z (рис. 3.1, а). Расстояние между этими силами () должно быть малым, чтобы можно было пренебречь моментом, создаваемым этими силами.

Применив метод сечений (разрезав стержень между силами P), можно легко установить, что в поперечном сечении стержня возникает только одно внутреннее усилие – поперечная

Сдвиг (механика)

Деформация сдвига

Сдвиг — в сопротивлении материалов — вид продольной деформации бруса, возникающий в том случае, если сила прикладывается касательно его поверхности (при этом нижняя часть бруска закреплена неподвижно).

Относительная деформация сдвига определяется по формуле:, где Δx — абсолютный сдвиг параллельных слоёв тела относительно друг друга; l — расстояние между слоями (для малых углов )

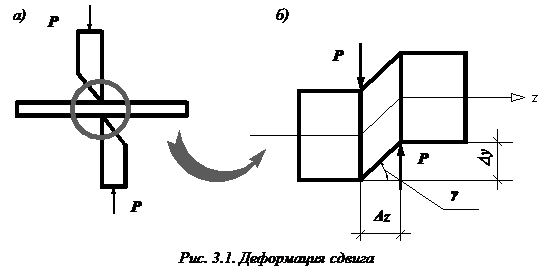Сдвиг- это вид деформации, при котором одна часть стержня смещается относительно другой (как скользят, например, карты в колоде). Деформация сдвига будет происходить, если к стержню приложить две равные по модулю противоположно направленные силы (P), перпендикулярные к его оси z (рис. 3.1, а). Расстояние между этими силами ( ) должно быть малым, чтобы можно было пренебречь мо ментом, создаваемым этими силами.

Применив метод сечений (разрезав стержень между силами P), можно легко установить, что в поперечном сечении стержня возникает только одно внутреннее усилие – поперечная сила  .

Далее мы увидим, что деформация сдвига возникает и при кручении стержня.