35. Напряжения.

Nz равномерно распределяется по площади поперечного сечения, вызывая нормальные напряжения. Из гипотезы плоских сечений следует: все продольные волокна стержня деформируются одинаково. Поэтому можно считать, что при растяжении (сжатии)напряжения во всех точках поперечного сечения стержня одинаковы и направлены по нормали к сечению. Такие напряжения, как уже отмечалось, называются нормальными напряжениями. Из вышеизложенного вытекает формула нормальных напряжений при растяжении (сжатии): где N – продольное усилие, возникающее в данном поперечном сечении стержня, а F – площадь этого поперечного сечения. Правило знаков для нормального напряжения ( ), как и для продольной силы (N): при растяжении нормальное напряжение считается положительным, а при сжатии – отрицательным. Напряжения.

Метод сечений позволяет выявить внутренние силовые факторы. Но для оценки прочности необходимо уметь определять внутренние силы в любой точке сечения рассматриваемого бруса. Поэтому введем числовую меру интенсивности внутренних сил - напряжение.

Рассмотрим брус, к которому приложена некоторая нагрузка. Брус под действием нагрузки находится в равновесии. Применяя метод сечений, рассечем брус поперечной плоскостью, отбросим левую часть бруса, заменим действие отброшенной части на рассматриваемую системой внутренних сил. Выделим вокруг произвольной точки малую площадку 

ΔА (рис. а). Равнодействующую внутренних сил в пределах этой площадки обозначим .ΔF

Отношение ΔF/ ΔА = p ср называется средним напряжением. Вектор среднего напряжения совпадает по направлению с вектором равнодействующей ΔF.

При постепенном уменьшении площадки ΔА изменяются как модуль, так и направление равнодействующей внутренних сил ΔF, а следовательно, вектор pср постепенно приближается к истинному значению напряжения p в заданной точке (рис. б). Числовое значение этого напряжения выражается равенством 

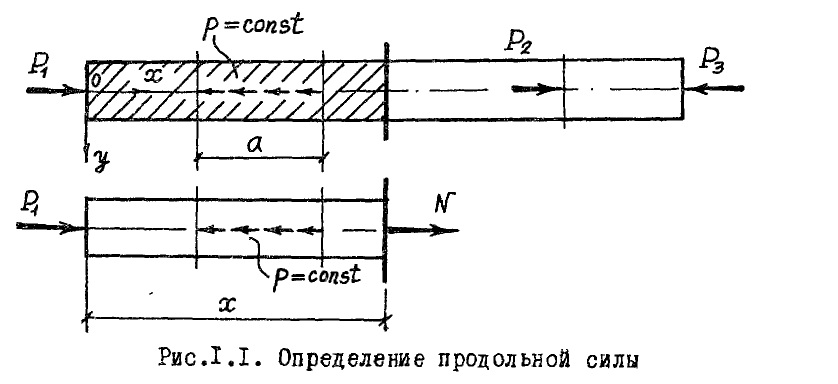
36. Растяжение и сжатие стержней.

Растяжение (сжатие) - это вид деформации стержня, при котором происходит изменение его первоначальной длины. Растяжение (сжатие) вызывается внешними силами, действующими вдоль оси стержня z. При этом в любом поперечном сечении стержня возникает только одно внутреннее усилие – продольная сила (N), которая является равнодействующей всех внутренних сил, возникающих в каждой точке этого сечения и направленных параллельно оси стержня.

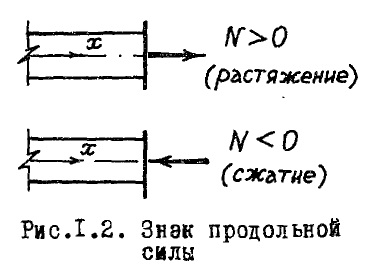
Растяжение-сжатие — в сопротивлении материалов — вид продольной деформации стержня или бруса, возникающий в том случае, стержня и проходит через его центр масс).

Детали

Называется также одноосным или линейным напряжённым состоянием. Является одним из основных видов напряжённого состояния параллелепипеда. Может быть также двух- и трёх-осным^[1]. Вызывается как силами, приложенными к концам стержня, так и силами, распределёнными по объёму (силы инерции и тяготения).

Растяжение вызывает удлинение стержня (также возможен разрыв и остаточная деформация), сжатие вызывает укорочение стержня (возможна потеря устойчивости и возникновение продольного изгиба).

В поперечных сечениях бруса возникает один внутренний силовой фактор — нормальная сила. Если растягивающая или сжимающая сила параллельна продольной оси бруса, но не проходит через неё, то стержень испытывает т. н. внецентренное растяжение (сжатие). В этом случае за счёт эксцентриситета приложения нагрузки в стержне кроме растягивающих (сжимающих) напряжений возникают ещё и изгибные напряжения.

Напряжение вдоль оси прямо пропорционально растягивающей или сжимающей силе и обратно пропорционально площади поперечного сечения. При упругой деформации между напряжением и относительной деформацией определяется законом Гука, при этом поперечные относительные деформации выводятся из продольных путём умножения их накоэффициент Пуассона. Пластическая деформация, предшествующая разрушению части материала, описывается нелинейными законами.