Главные моменты инерции плоской фигуры.
Момент инерции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Поворотом осей, можно найти такое их положение, при котором центробежный момент инерции Jzy равен нулю. Такие оси называют главными осями инерции.
Г
лавные
оси инерции, проходящие через центр
тяжести сечения, называют главными
центральными осями.
- Момент инерции
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n
материальных точек системы на квадраты их расстояний до оси:
где: mi — масса i-й точки, ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении:
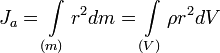
где: dm = pdV масса малого элемента объёма тела dV,
P – плотность
r- растояние от элемента dV до оси а
28.и 29. Центр тяжести. Геометрические характеристики плоской фигуры.
30 Определение координат центра тяжести плоских и пространственных фигур.
При решении задач обычно пользуются методом Разбиения. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны либо легко находятся. Например, изображённую деталь можно представить в виде двух плоских фигур с площадями S1 и S2 (S = S1 + S2). Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны: рис1 Координаты центра тяжести объемного тела постоянной плотности находятся по формулам: XC=∑xiVi∑ViYC=∑yiVi∑ViZC=∑ziVi∑Vi где xi yi zi – координаты центров тяжести элементарных частей, Vi – объем i-й части. Если тело представляет собой однородную пластину постоянной толщины, то координаты ее центра тяжести: XC=∑xiSi∑SiYC=∑yiSi∑Si где Si – площадь i-го элемента. Для стержневых конструкций, образованных стержнями одинаковой плотности и постоянного поперечного сечения, координаты центра тяжести определяются по формулам: XC=∑xili∑liYC=∑yili∑li где li – длина элемента линии.
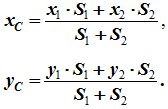
Исходя из полученных ранее общих формул, можно указать способы определения координат центров тяжести твердых тел:
1. Аналитический (путем интегрирования).
2. Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
3. Экспериментальный (метод подвешивания тела).
4. Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S1 и S2 (S = S1 + S2). Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны:
Рисунок 1.8
5 . Дополнение (метод отрицательных площадей или объемов). Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
Рисунок 1.9
Центры тяжести простейших фигур
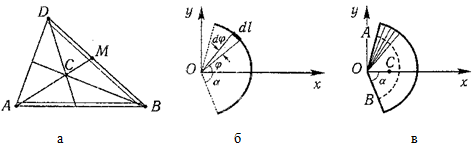
1 Треугольник
Центр тяжести площади треугольник совпадает с точкой пересечения его медиан (рисунок а).
DM = MB, CM = (1/3)AM.
2 Дуга окружности
Дуга имеет ось симметрии (рисунок б). Центр тяжести лежит на этой оси, т.е. yC = 0.
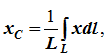
dl – элемент дуги, dl = Rdφ, R – радиус окружности, x = Rcosφ, L = 2αR,
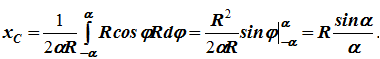
Следовательно: xC = R(sinα/α).
3 Круговой сектор
Сектор радиуса R с центральным углом 2α имеет ось симметрии Ox, на которой находится центр тяжести (рисунок в).
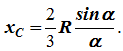Разбиваем сектор
на элементарные секторы, которые можно
считать треугольниками. Центры тяжести
элементарных секторов располагаются
на дуге окружности радиуса (2/3)R.
Центр тяжести сектора совпадает с центром тяжести дуги AB: