17. Теплоёмкость.

Теплоемкостью какого-либо тела наз. величина, равная кол-ву тепла, которое нужно сообщить телу , чтобы повысить его тем-ру на 1 кельвин. (дж/К)

Теплоемкость моля вещества наз. молярной теплоемкостью, обозначают (С=Дж/моль*К)

Теплоемкость единицы массы вещества наз. удельной теплоемкостью, обозначают (с=С/М где

М - молярная масса). Величина теплоемкости зависит от условий, при которых происходит нагревание тела. Различают теплоемкость при постоянном объёме Сv , и при постоянном давлении Ср. Между удельной и молярной теплоёмкостью имеется соотношение с=С/М.

18. Характерные скорости движения молекул газа. Вычисление средних скоростей в статической физики.

По определению среднее значение какой-то величины, которая случайным образом в N независимых испытаниях принимает N значений a_i, равно

Ввиду полной хаотичности движения молекул проекции скорости молекул на ось x с равной вероятностью могут принимать как положительные, так и отрицательные значения. Поэтому среднее значение проекции скорости i-ой молекулы на ось x равно нулю: <vix>=0. Аналогично <v_iy>=<v_iz>=0. Однако средние значения квадратов проекций скорости не равны нулю! Определим для i-ой молекулы

v_i² = v_ix² + v_iy² + v_iz².

Тогда

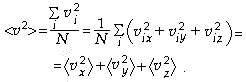
Поскольку все направления эквивалентны, то

<v_x²> = <v_y²> = <v_z²>,

поэтому

< v_x²> = < v²>/3.

Уравнение среднеквадратичной скорости молекулы легко выводится из основного уравнения МКТ для одного моля газа.

, для 1 моля N = N_a, где N_a — постоянная Авогадро

N_am = M_r, где M_r — молярная масса газа

Отсюда окончательно

19. Принцип относительности в классической и релятивистской механике. Постулаты Эйнштейна. Преобразования Лоренца.

Механический принцип относительности Галилея.

При описании физических явлений мы всегда пользуется какой-либо системой отсчета. Например, движение тел мы чаще всего рассматриваем относительно земли, т.е. условно принимаем земной шар за неподвижное тело.

Галилей показал, что в условиях земли практически справедлив закон инерции. Такую систему отсчета, в которой выполняется закон инерции стали называть инерциальной. Теперь рассмотрим две системы отсчета, движущиеся друг относительно друга с постоянной скоростью V0 . Одну из этих систем, обозначенную на рисунке буквой К будем условна считать неподвижной. Тогда вторая система К' будет двигаться прямолинейно и равномерно.

Найдем связь между координатами x,y,z некоторой точки Р в системе К и координатами x',y',z' так же точки в системе К'. Если начать отсчет времени с того момента, когда начала координат обеих систем совпадали, то x=x'+v0t (1). Кроме того, что y=y' и z=z' (2).

Добавив и этим соотношениям принятое в классической механике предположение, что время в обоих системах течет одинаковым образом, т.е. что t=t', и получим совокупность четырех уравнений: x=x'+v0 t ; y=y'; z=z' ; t=t' (3); называемых преобразованием Галилея.

Продифференцировав эти отношения, найдем связь между скоростями точки Р по отношению и системам отсчета К и К': (4); (5); (6) или (7), ; (8). Эти соотношение дают правило сложения скоростей в классической механике. С одним словом Г. Галилей ввел в классическую механику принцип относительности, смысл которого следующий: никакими механическими опытами нельзя установить, покоится инерциальная система отсчета или движется равномерно и прямолинейно.

Все выше сказанное справедливo лишь при значениях , малых сравнению со скоростью света в вакууме, которую мы будем обозначать буквой С . При больших скоростях , сравнимых с С, для изучения движения тел, создали новая механика, которая включить себя классическую механику Ньютона как частный, предельный случай и называли релятивистической механикой.

Постулаты специальной теории относительности.

Для описания движений, совершающихся со скоростями, с равными с. С, Эйнштейн создал релятивистическую механику, т.е. механику, учитывающую требование специальной теории относительности.

Основу этой теории образуют два постулата, которые носят названия принципа относительности Эйнштейна и принципа постоянства скорости света. Согласно принципа относительности Эйнштейна все законы природы одинаковы во всех инерциальных системах отсчета.

Принцип постоянства скорости света утверждает, что скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приёмников света.

Преобразование Лоренца.

Рассмотрим две инерциальные системы отсчета, которые мы обозначим К и К'. рис. Предположим, система координат К' движется относительно системы К с постоянной скоростью v . Распространение светового сигнала в положительном направлении оси х описывается уравнением: (9). Для системы координат К' аналогичное уравнение имеет вид: (10).

Движению, происходящему в обеих системах координат, должны удовлетворять как уравнение (9), так и уравнение (10), что выполняется, если имеет место соотношение: (11), где l-постоянная величина. Для лучей, распространяющихся в отрицательном направлении оси Х, уравнение (11) имеет вид: (12), где m-постоянная величина. Введем новые постоянные: (13), (14). Тогда, (15), (16). Определим постоянные а и в.

Для начала координат системы К' имеем x'=0, тогда (16) или (17). Если в уравнение (15) положить t=0, t0 x'=ax (18) . Из этого следует, что если некоторый отрезок в системе К' равен единице то, наблюдая его из системы К, мы обнаружим, что (19). Если в системе К', t'=0, то и (20). Так как оба наблюдения должны быть идентичными, то , или (21). Это равенства определяют постоянные а и в. Подставляя их значения в уравнения (15) и (16), получаем: (22) и времени: (23).К этим соотношениям можно добавить уравнения y'=y, z'=z (24).< br>

Рассмотрим некоторые выводы из теории относительности, вытекающие из преобразования Лоренца.

1. Из преобразований Лоренца для координат х и x' и времени t и t' следует, что . В противном случае эти координаты и времена окажутся мнимыми. Скорость v относительного движения двух инерциальных систем отсчета не может превосходить скорости света в вакууме.

2. Пусть стержень MN движется вместе с системой отсчета K' относительно системы К. рис. Длина стержня в системе К' равна: (25). Длина тела в системе отсчета, где оно покоится , называется собственной длиной. Для определения длины движущегося стержня в системе К необходимо найти координаты х2 и х1 точек N и M конца и начала стержня в один и тот же момент времени по часам в системе К': (26). Из преобразований Лоренца следует, что (27), или (28). Длина тела зависит от скорости его движения. Собственная длина тела является его наибольшей длиной. Линейный размер тела, движущегося относительно инерциальной системы отсчета уменьшается в раз. Из преобразований Лоренца следует, что и (29), т.е. поперечные размеры тела не зависит от скорости его движения и одинаковы во всех инерциальных системах отсчета.

3. Время измеряемое в системе отсчета, где точка неподвижна, назы-вается собственным временем. В системе К, относительно которой система К' движется промежуток времени t между событиями будет: t=t2 -t1 (30), где время отсчитано по часам в системе К. Из преобразований Лоренца для времени: (31) и (32). Следует , что 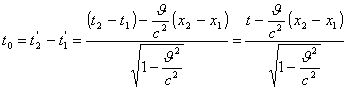(33). Но смещение точки вдоль оси ОХ системы К за время t: и (34), т.е. или (35). Длительность явления, происходящего в некоторой точке пространства, будет наименьшей в той инерциальной системе отсчета, относительно которой эта точка неподвижна эта означает, что часы движущиеся относительно инерциальной системы отсчета, идут медленнее неподвижных часов и показывает меньший промежуток времени между событиями.

4. Релятивистский закон сложения скоростей. Если материальная точка движется вдоль осей ОХ и О'X' в инерциальных системах К и К' и имеет в этих системах скорости , равные соответственно v и v' , то (36), где V- скорость движения системы К'относительно системы К.

Релятивистская динамика.

Одним из основных законов классической механики является закон сохранения количества движения: . В релятивистская динамики масса тела определяется по формуле: (37), где - . Выражение импульса в соответствии с (37) имеет более сложный вид: (38). Тогда уравнение релятивистской динамики будет иметь вид: (39). Энергии движущегося тела в релятивистской динамике растет его со скоростью быстрее, чем в классической механике. Однако возрастание энергии, так же как и в классической механике, вызывается работой силы F: (40).Отсюда (41). Подставляя (37) в (41) получим: (42), откуда после интегрирования получим: (43). Если приравнять постоянную интегрирования нулю, то получим энергию, эквивалентную массе покоя, т.е. (44). Полная энергия движущегося тела равна: (45). Эта уравнение выражает закон взаимосвязи массы и энергии: полная энергия системы равна произведению ее полной релятивистской массы на квадрат скорости света в вакууме.