2.2. Вычисление определителей

В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы. Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись.

Мы не будем давать строгое математическое определение определителя, и, вообще, будем стараться минимизировать математическую терминологию, так как большинству читателей легче от этого не станет. Наша задача – научить Вас решать определители второго, третьего и четвертого порядка.

Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.

Определение: Определитель, или детерминант матрицы, – это единственное для данной матрицы число, оно определяется всеми элементами матрицы и характеризует всю матрицу. Определитель можно вычислить только для квадратной матрицы.

Для вектора таким характерным числом является модуль вектора. Для действительного числа произвольного знака таким характерным числом является абсолютное значение, или модуль числа. Но, в отличие от модуля ненулевого вектора или числа, определитель матрицы может иметь любой знак и быть равным нулю, в том числе для ненулевой исходной матрицы.

Обозначение: Определитель матрицы обозначается символом данной матрицы в прямых (одинарных, или двойных) скобках, как у модуля вектора, или D, или Δ, или det(A). Т. е., как |A|, или ||A||, или латинской буквой D, или греческой буквой Δ, или det(A) для матрицы A. При этом вместо A в новые скобки может быть вписана вся таблица.

На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .

Определитель четвертого порядка встречается значительно реже, но о нем тоже поговорим.

Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании в строке или столбце D речи не идет. Менять местами числа нельзя! Но если очень хочется, то можно... (На самом деле, есть десяток теорем о детерминантах, об условиях, при которых можно переставлять строки и столбцы, но не отдельные элементы, определителя со сменой (или без смены) знака определителя).

Таким образом, если дан определитель, то ничего внутри него не трогаем!

1) Что значит вычислить (найти, раскрыть, решить) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса (?) в вышерассмотренных примерах – это совершенно обыкновенные числа.

2) Теперь осталось разобраться в том, КАК найти это число. Как Вы догадываетесь, для этого нужно применить определенные правила, формулы и алгоритмы.

Определитель матрицы «два на два», его формула:

.

ЭТО НУЖНО ЗАПОМНИТЬ, по крайней мере, на время изучения высшей математики в ВУЗе. Сразу рассмотрим пример:

Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.

Определитель матрицы «три на три», его формула:

Пример:

Приведенная формула определителя «три на три» длинная и допустить ошибку по невнимательности проще простого. Как избежать промахов? Определитель «три на три» можно раскрыть 10 способами (10-ю способами получить приведённую формулу). Четыре из них – «простые», и шесть – «нормальные».

Начнем с четырёх простых способов «параллельных полосок» Саррюса:

1) два способа дополнительных столбцов;

2) два способа дополнительных строк.

Первый способ дополнительных столбцов состоит в том, что справа от определителя приписывают первый и второй столбцы и аккуратно карандашом проводят линии:

.

Заметим, что элементы на «красных» диагоналях входят в формулу со знаком «плюс», а элементы на «синих» диагоналях входят в формулу со знаком минус.

Пример:

Второй способ дополнительных столбцов состоит в том, что слева, перед определителем приписывают второй и третий (ближе к определителю) столбцы и проводят линии, начиная с главной диагонали.

Первый способ дополнительных строк состоит в том, что снизу от определителя приписывают первую (ближе к определителю) и вторую строки и проводят линии, начиная с главной диагонали.

Второй способ дополнительных строк состоит в том, что сверху от определителя приписывают вторую и третью (ближе к определителю) строки и проводят линии, начиная с главной диагонали.

Во всех четырёх простых способах элементы матрицы, находящиеся на «красных» диагоналях, параллельных главной диагонали, входят в формулу со знаком «плюс». Элементы матрицы, находящиеся на «синих» диагоналях, входят в формулу со знаком минус. Вычисления по остальным простым способам проведите самостоятельно.

Сравните решение «по формуле» и «простые решения». Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.

Теперь рассмотрим 6 «нормальных» способов для вычисления определителя. Почему «нормальных» Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.

Как Вы заметили, у определителя «три на три» три столбца и три строки. Вычислить определитель можно, разложив его по любой строке или по любому столбцу. Таким образом, получается 6 способов, при этом во всех случаях используется алгоритм одного и того же типа (смотрите в книгах по высшей алгебре теорему Лапласа о разложении определителя матрицы по любой строке или столбцу, но мы обещали нашим студентам «не докучать моралью строгой»).

Теорема Лапласа: Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно?

Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.

В следующем примере будем раскрывать определитель по первой строке.

Для этого нам понадобится «матрица знаков»: . Легко заметить, что знаки расположены в шахматном порядке.

Примечание: Внимание! «Матрица знаков» – это изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает вам понять алгоритм вычисления определителя.

Сначала приведём полное решение. Снова берем наш подопытный определитель и проводим вычисления по теореме Лапласа, разложив его по первой строке:

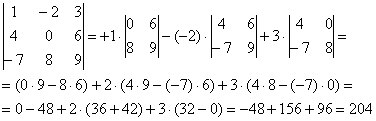
И главный вопрос: КАК из определителя «три на три» получить вот это вот:

?

Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или, как их еще называют, МИНОРОВ. Термин надо запомнить. Минор – маленький, точнее, по смыслу в данном случае, - определитель уменьшенной матрицы.

Коль скоро выбран способ разложения определителя по первой строке, очевидно, что всё вращается вокруг неё. Запишем рядом исходную матрицу и «матрицу знаков», одинаковую для любой матрицы «три на три»:

Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец). Сначала разбираемся с первым элементом строки, то есть с единицей:

1) Из матрицы знаков выписываем соответствующий знак:

2) Затем записываем сам элемент:

3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:

Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).

Переходим ко второму элементу строки.

4) Из матрицы знаков выписываем соответствующий знак:

5) Затем записываем второй элемент:

6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:

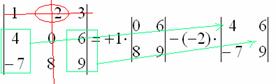
Оставшиеся четыре числа записываем в маленький определитель.

Переходим к третьему элементу первой строки. Никакой оригинальности:

7) Из матрицы знаков выписываем соответствующий знак:

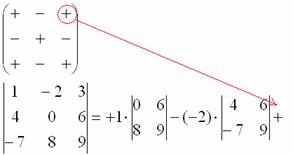
8) Записываем третий элемент:

9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:

Оставшиеся четыре числа записываем в маленький определитель.

Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!

Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым. В этом и состоит ценность теоремы Лапласа!

Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм. При этом матрица знаков у нас увеличится:

В следующем примере раскроем определитель по четвертому столбцу:

Пример:

А как это получилось, попробуйте разобраться самостоятельно. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше будет также раскрыть определитель по какому-нибудь другому столбцу или другой строке.