Приклади розв’язку задач

Приклад 1. Рівняння руху матеріальної точки уздовж осі має вид , де A = 2 м, B = –2 м/с, C = 0,5 м/с³. Знайти координату, швидкість і прискорення точки в момент часу t = 3 с. Знайти середні значення швидкості і прискорення у проміжок часу від 1 с до 3 с.

Дано: ; A = 2 м, B = –2 м/с, C = 0,5 м/с³; t = 3 с, t₁ = 1c, t₂ = 3 c.

Знайти: , , , , .

Розв’язок. Координату х знайдемо, підставивши в рівняння руху числові значення коефіцієнтів А, В, С і часу t.

Миттєва швидкість щодо осі х – це перша похідна від координати за часом:

. (1)

Миттєве прискорення точки знайдемо, узявши першу похідну від швидкості за часом:

. (2)

Обчислення.

Для моменту часу t = 2 с одержимо

x = (2 – 2ּ3 + 0,5·3³) (м) = 9,5 м;

= (–2 + 3·0,5·3²) м/с= 11,5 м/с;

a₁ = (6·0,5·3 )м/с² = 9 м/с².

Середня швидкість визначається відношенням

,

де х₁ = 2 – 2t₁ + 0,5t₁³ = 0,5 м; х₂ = 2 – 2t₂ + 0,5t₂³ = 9,5 м/с.

Тоді

м/с.

Середнє прискорення визначається за формулою , згідно (1)

–2 + 3·0,5 = –0,5 м/с, –2 +3·0,5 = 11,5 м/с.

Тоді

м/с².

Відповідь: x = 9,5 м; = 4,5 м/с; a = 6 м/с².

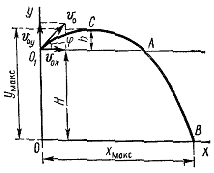
Приклад 2. Тіло кинуте з висоти 12 м під кутом 30⁰ до горизонту з початковою швидкістю 12 м/с. Визначити тривалість польоту тіла до точок A і B (рис. 1.1), максимальну висоту, на яку піднімається тіло, і дальність польоту тіла. Опір повітря не враховувати.

Дано: H = 12 м; α = 300; 12 м/с. Знайти: tА, tВ, hmax, xmax. Розв’язок. У системі координат, показаній на рис. 1.1, проекції початкової швидкості на осі координат дорівнюють: ; (1) ; (2) Координати тіла з часом змінюються

Рис. 1.1.

відповідно до рівняння рівнозмінного (вздовж осі y) та рівномірного (вздовж осі x) руху

; (3)

. (4)

Час підйому тіла знайдемо за умови, що в найвищій точці підйому тіла вертикальної складової його швидкості . Тоді з виразу (2) знайдемо час t_п, що пройшов до підйому тіла на максимальну висоту

. (5)

Час спуску тіла від точки C до точки A дорівнює часу підйому, тому тривалість польоту тіла від точки O₁ до точки A дорівнює

. (6)

Максимальну висоту підйому знайдемо з рівняння (4), підставивши в нього час підйому з рівняння (5)

. (7)

Час польоту тіла до точки В знайдемо, розв’язуючи квадратне рівняння (нефізичний розв’язок відкидається), отримане з виразу (4), у якому кінцева координата y(t) прирівнюється до нуля

. (8)

Дальність польоту знайдемо з рівняння (3), підставивши в нього час руху з рівняння (8)

. (9)

Обчислення.

t_А = 2·12·sin30⁰/9,81 = 1,22 с.

t_В = = 2,29 c.

H_max = 12 + (12·sin30⁰)²/(2·9,81) = 13,84 м;

x_max = 12·2,29·cos30⁰ = 23,8 м.

Відповідь: t_А = 1,22 с; t_В = 2,99 с; H_max = 13,84 м; x_max = 23,8 м.

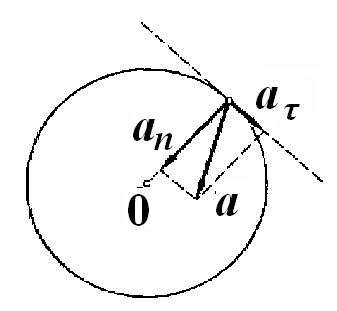
Приклад 3. Тіло обертається навколо нерухомої осі за законом x = A + Bt + Ct², де A = 10 рад, B = 20 рад/с, С = –2 рад/с². Знайти повне прискорення точки, що знаходиться на відстані r = 0,1 м від осі обертання, для моменту часу t = 4 с.

Дано: x = A + Bt + Ct², A = 10 рад, B = 20 рад/с, C = –2 рад/с²; r = = 0,1 м; t = 4 с.

Знайти: a(t).

Розв’язок. Повне прискорення точки, що рухається по кривій лінії, може бути знайдене як геометрична сума тангенціального прискорення , спрямованого по дотичній до траєкторії, і нормального прискорення , спрямованого до центра кривизни траєкторії (рис. 1.2):

Рис. 1.2.

.

Оскільки вектори і взаємно перпендикулярні, модуль повного прискорення дорівнює

. (1)

Модулі тангенціального і нормального прискорень тіла, що обертається, виражаються формулами ; , де – модуль кутової швидкості тіла; – модуль його кутового прискорення.

Підставляючи вираз і у формулу (1), знаходимо

. (2)

Кутову швидкість знайдемо, узявши першу похідну кута повороту за часом t: .

Кутове прискорення знайдемо, узявши першу похідну від кутової швидкості за часом: .

У момент часу t = 4 с:

рад/с = 4 рад/с; рад/с².

Обчислення.

Підставляючи значення , і r у формулу (2), одержуємо

= 1,65 м/с².

Відповідь: a = 1,65 м/с².

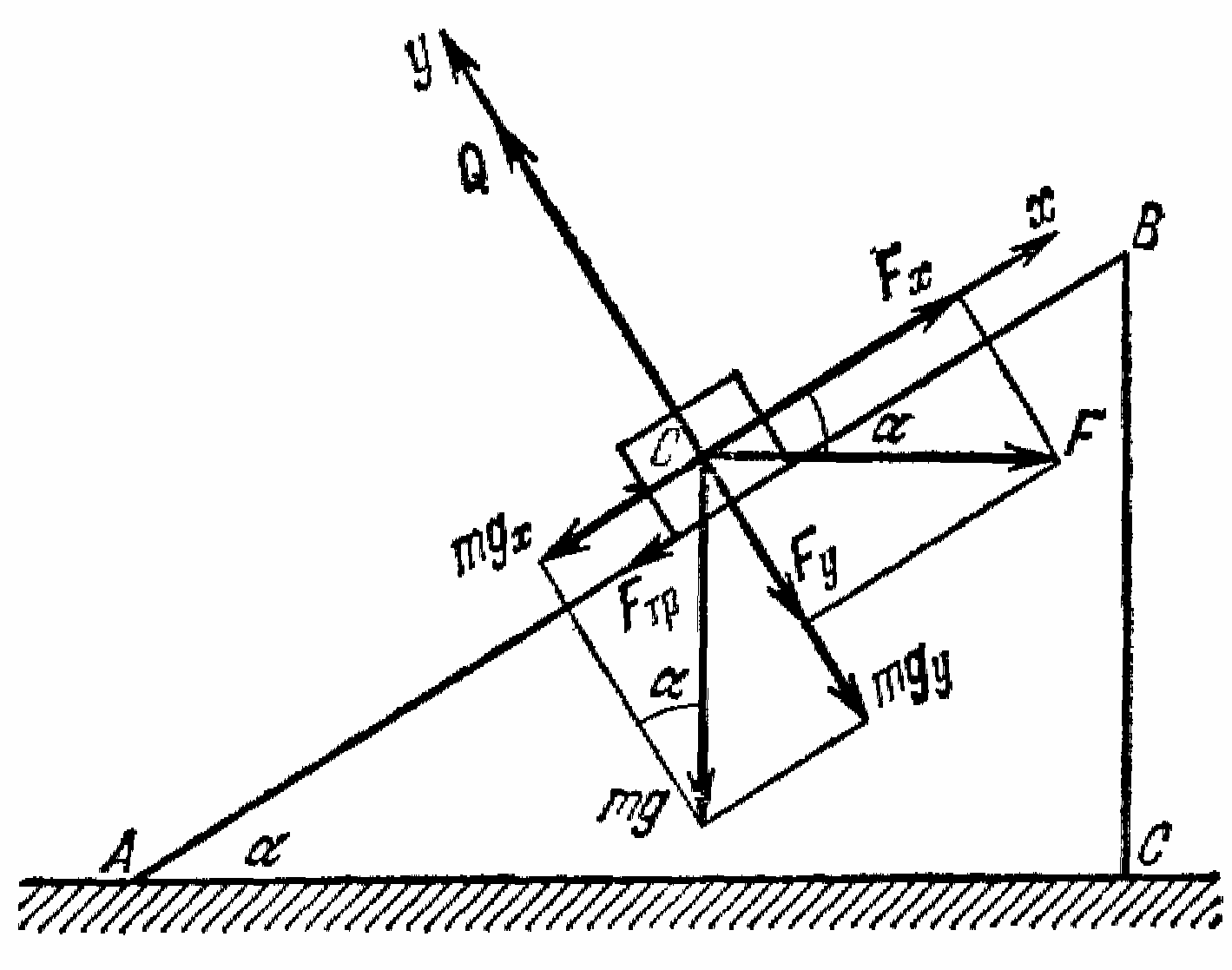
Приклад 4. На тіло масою 100 кг, що лежить на похилій площині, яка утворює кут 40⁰ з горизонтом, діє горизонтальна сила 1500 Н (рис. 1.3). Визначити прискорення, з яким рухається тіло, якщо коефіцієнт тертя дорівнює 0,1.

Дано: m = 100 кг; F = 1500 Н; 400; 0,1. Знайти: a. Розв’язок. Виберемо напрямок координатних осей так, щоб одна з них була спрямована уздовж похилої площини (Ox), а інша – перпендикулярно до неї (Oy). На тіло діють сила F – паралельно до основи похилої площини, сила ваги mg – вертикально вниз, реакція

Рис. 1.3.

опори Q – перпендикулярно до похилої площини, і сила тертя F_тр – уздовж похилої площини вбік, протилежний рухові.

Запишемо другий закон Ньютона у векторній формі

. (1)

Для переходу до скалярної форми знайдемо проекції всіх діючих сил на координатні осі. Складові сили F на осі координат дорівнюють

; . (2)

Складові сили ваги mg на осі координат дорівнюють

; . (3)

Сила Q діє тільки уздовж осі Oy, а сила тертя F_тер – протилежно до осі Ox.

Оскільки в напрямку Oy складова прискорення дорівнює нулю, з (1) – (3) виходить

. (4)

Проекція рівняння (1) на вісь (Ox) у цьому випадку має вид

. (5)

Сила тертя дорівнює добуткові сили нормального тиску тіла N на коефіцієнт тертя

. (6)

Оскільки сила N за третім законом Ньютона дорівнює силі Q

. (7)

Таким чином, з (5)–(7) можна одержати остаточний вираз для прискорення a

. (8)

Обчислення.

Підставляючи значення , і r у формулу (8), одержуємо

м/с².

Відповідь: a = 3,4 м/с².

Приклад 5. Тіло масою 1 кг рухається по прямій відповідно до рівняння x = 2t² + 4t + 1. Визначити роботу, яку виконує постійна сила за перші 10 с після початку руху, і залежність кінетичної енергії тіла від часу.

Дано: x = 2t² + 4t + 1; m = 1 кг; t = 10 с.

Знайти: A; T = T(t).

Розв’язок. Робота A може бути визначена за допомогою криволінійного інтеграла від потужності P у заданому проміжку часу

. (1)

При прямолінійному русі потужність можна знайти як добуток діючої сили F на швидкість тіла

. (2)

Швидкість знайдемо як першу похідну за часом від координати тіла

. (3)

Силу можна визначити за допомогою другого закону Ньютона

, (4)

де a – прискорення тіла, що знайдемо як першу похідну за часом від його швидкості

. (5)

Підставляючи вираз (2)–(4) у (1) і інтегруючи в зазначених границях, одержимо

. (5)

Кінетичну енергію тіла знайдемо з визначення за допомогою виразу (3) для швидкості

. (6)

Обчислення.

A = 8·1·(10+2)·10 = 960 Дж.

Відповідь: A = 960 Дж; T = 8m(t + 1)².

Приклад 6. При пострілі з пружинного пістолета вертикально нагору куля масою 20 г піднялася на висоту 5 м. Визначити жорсткість пружини пістолета, якщо вона була стиснута на 10 см. Масою пружини і силами тертя знехтувати.

Дано: m = 0,02 кг; h = 5 м; x = 0,1 м.

Знайти: k.

Розв’язок. Розглянемо систему «пружина – куля». Оскільки на тіла системи діють тільки консервативні сили, то для розв’язку задачі можна застосувати закон збереження енергії в механіці. Відповідно до нього, повна механічна енергія E₁ системи в початковому стані (у даному випадку перед пострілом) дорівнює повній енергії E₂ у кінцевому стані (коли куля піднялася на висоту h), тобто E₁ = E₂, або

T₁ + W₁= T₂ + W₂, (1)

де T₁, T₂, W₁ і W₂ – кінетичні і потенційні енергії системи у початковому і кінцевому станах. Оскільки кінетичні енергії кулі у початковому і кінцевому станах дорівнюють нулеві, то рівність (1) набуває виду

W₁ = W₂, (2)

Приймемо, що потенціальна енергія кулі в полі сил тяжіння Землі, знаходячись в стані спокою на стиснутій пружині, дорівнює нулю, а висоту підйому кулі будемо відраховувати від торця стиснутої пружини. Тоді енергія системи у початковому стані буде дорівнювати потенціальній енергії стиснутої пружини, тобто , а в кінцевому стані – потенціальній енергії кулі на висоті h, тобто W₂ = mgh.

Підставивши вираз W₁ і W₂ у формулу (2), знайдемо

. (3)

Обчислення.

k = 2·0,02·9,81·5/(0,1) = 196 Н/м.

Відповідь: k = 196 Н/м.

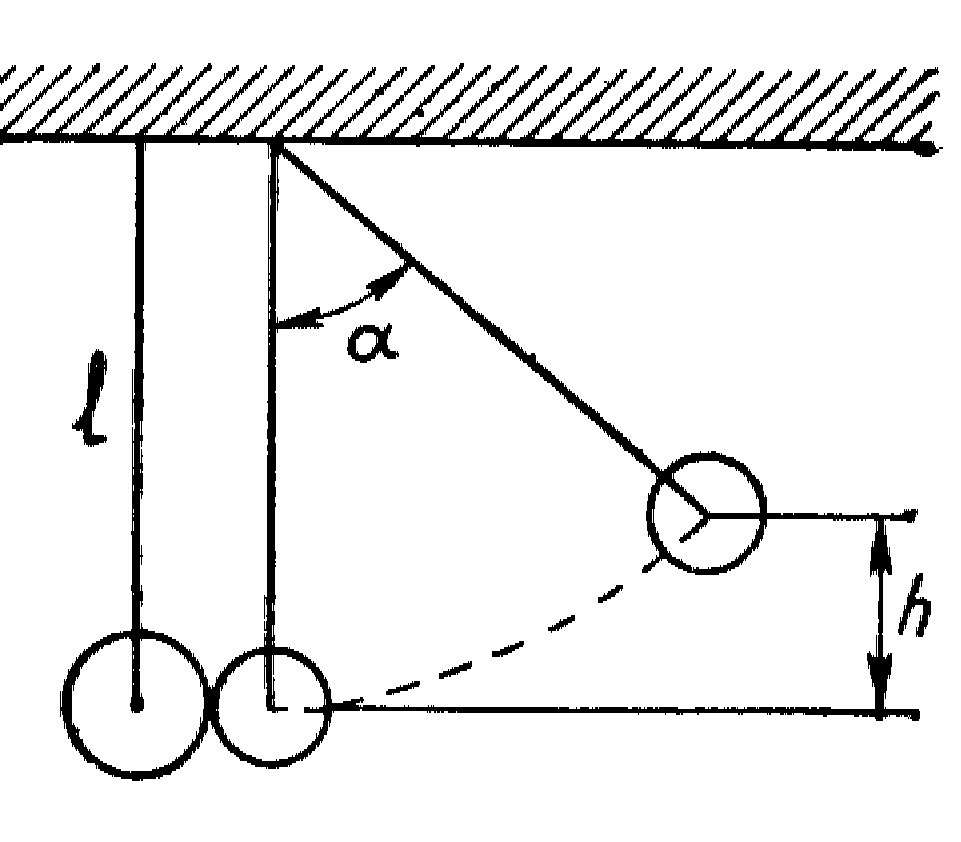
Приклад 7. На двох шнурах однакової довжини по 0,8 м підвішено дві свинцевих кулі масами 0,5 і 1 кг (рис. 1.4). Кулі стикаються між собою. Кулю меншої маси відвели вбік так, що шнур відхилився на кут = 600, і відпустили. На яку висоту піднімуться обидві кулі після зіткнення? Удар вважати центральним і абсолютно непружним. Визначити енергію, витрачену на деформацію куль при ударі.

Рис. 1.4.

Дано: m₁ = 0,5 кг, m₂ =1 кг; = 60⁰; l = 0,8 м, = 0.

Знайти: h; ∆E.

Розв’язок. Оскільки удар куль непружний, то після взаємодії вони будуть рухатися з однаковою загальною швидкістю u. При такому ударі виконується тільки закон збереження імпульсу:

, (1)

де і – швидкості куль до удару.

Швидкість великої кулі до удару дорівнює нулю. Швидкість меншої кулі знайдемо, використовуючи закон збереження енергії. При відхиленні меншої кулі на кут (рис. 1.4) їй надається потенціальна енергія, яка потім переходить у кінетичну. Безпосередньо перед ударом кінетична енергія цієї кулі дорівнює вихідній потенціальній енергії

, (2)

де h₁ – максимальна вихідна висота підйому першої кулі.

Висоту h₁, як видно з рисунка, можна знайти з виразу

. (3)

З формул (2) і (3) знайдемо

. (4)

З рівнянь (1) і (4) знаходимо швидкість куль після удару

. (5)

Кінетична енергія, якою володіють кулі після удару, переходить у їхню потенціальну енергію

, (6)

де h – максимальна висота підняття куль після зіткнення.

З формул (5) і (6) знаходимо

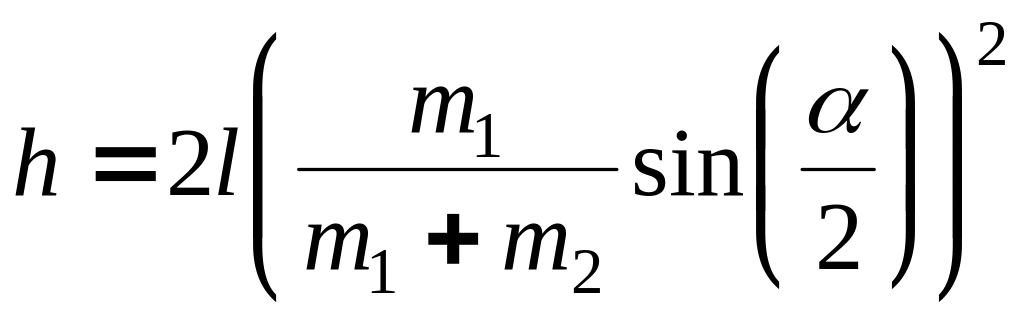. (7)

При непружному ударі куль частина енергії витрачається на їх деформацію. Енергія деформації визначається різницею кінетичних енергій до і після удару

. (8)

Обчислення.

= 0,044 м.

= 1,3 Дж.

Відповідь: h = 0,044 м; ∆E = 1,3 Дж.

Приклад 8. Молот масою 70 кг падає з висоти 5 м і вдаряє по залізній поковці, що лежить на ковадлі. Маса кувалди разом з поковкою 1330 кг. Вважаючи удар абсолютно непружним, визначити енергію, що витрачається на деформацію виробу. Систему молот-поковка-ковадло вважати замкненою.

Дано: m₁ = 70 кг, m₂ =1330 кг; h = 5 м.

Знайти: E_Д.

Розв’язок. За умовою задачі система молот-поковка-ковадла вважається замкненою, а удар непружний. На підставі закону збереження енергії можна вважати, що енергія, витрачена на деформацію поковки, дорівнює різниці значень механічної енергії системи до і після удару.

Вважаємо, що під час удару змінюється тільки кінетична енергія тіл, тобто незначним переміщенням тіл по вертикалі під час удару нехтуємо. Тоді для енергії деформації виробу маємо

, (1)

де u – загальна швидкість усіх тіл системи після непружного удару, а  – швидкість молота наприкінці падіння з висоти h.

Швидкість легко знайти, тому що початкова потенціальна енергія молота (на висоті h) дорівнює його кінетичній енергії безпосередньо перед ударом об поковку

. (2)

Зауважимо, що для даної системи виконується закон збереження імпульсу

. (3)

З виразу (2) можна знайти швидкість , а потім з виразу (3) – швидкість u

; (4а)

. (4б)

Підставляючи вираження (4) у (1), тепер легко одержати остаточну формулу

.

Обчислення.

= 325,85 Дж.

Відповідь: E_Д = 325,85 Дж.

Приклад 9. Яку мінімальну швидкість потрібно надати ракеті, щоб вона, стартуючи з Землі, назавжди залишила її? Опором повітря знехтувати.

Дано: R₃ = 6,37·10⁶ м; g = 9,81 м/с²; R → ∞.

Знайти: .

Розв’язок. Відповідно до умови задачі система Земля-ракета є замкненою і консервативною. Тому можна застосувати закон збереження повної механічної енергії ракети

, (1)

де m – маса ракети; M – маса Землі; – швидкість ракети; r – відстань між ракетою і центром Землі.

У початковій точці (на поверхні Землі) швидкість ракети , а r = R₃. Для того, щоб ракета не повернулась на Землю, очевидно, у кінцевий момент часу слід покласти: ; . Цьому станові, як випливає з виразу (1), відповідає повна механічна енергія ракети, що дорівнює нулю. Таким чином, і початкова енергія ракети буде дорівнювати нулю

. (2)

Відповідно до закону всесвітнього тяжіння на поверхні Землі сила притягання дорівнює

, (3)

звідки випливає корисне співвідношення

. (4)

Таким чином, підставляючи виразу (4) у (1), одержимо остаточно

. (5)

Обчислення.

м/с.

Відповідь: 11,2 км/с.

Приклад 10. Маховик, маса якого рівномірно розподілена по ободу з радіусом 40 см, вільно обертався з частотою 720 об/хв. навколо горизонтальної осі, що проходить через його центр симетрії. Потім на маховик почав діяти постійний гальмуючий момент сил, внаслідок чого він зупинився через 30 с. Знайти гальмуючий момент сил і число оборотів, що зробив маховик за цей час, якщо його маса 4 кг.

Дано: n₀ = 720 об/хв = 12 об/с; n_τ = 0; m = 4 кг; R = 0,4 м; t = 30 с.

Знайти: M; N.

Розв’язок. Рух маховика підкоряється рівнянню динаміки обертального руху, що при постійному моменті сил M має вид

. (1)

Тут J – момент інерції маховика, – зміна його кутової швидкості за проміжок часу Δt. Для розглянутого випадку ці величини визначаються такими формулами

; (2)

; (3)

, (4)

де , .

Підставляючи ці вирази в (1), знайдемо пошукуваний момент сил

. (5)

Число оборотів, виконаних маховиком, пов’язано з повним кутом повороту маховика виразом

. (6)

Для того, щоб знайти скористаємося тим, що зміна кінетичної енергії маховика дорівнює роботі, яка виконаній гальмуючим моментом сил

, (7)

або

. (8)

Таким чином, з виразу (5)–(8) можна остаточно одержати:

. (9)

Обчислення.

M = 2·3,14·4·0,4²·(0 – 12)/30 = –1,61 Н;

N = (0 + 12)·30/2 = 180.

Відповідь: M = –1,61 Н; N = 180 оборотів. Знак «–»указує на те, що момент сил гальмуючий.

Приклад 11. Через блок у вигляді суцільного диска, що має масу 80 г (рис. 1.5), перекинуто тонку гнучку нитку, до кінців якої підвішено вантажі з масами 100 г і 200 г. Визначити прискорення, з яким будуть рухатися вантажі, якщо їх полишити н самих себе. Тертям і масою нитки знехтувати. Дано: m = 0,08 кг; m1 = 0,1 кг; m2 = 0,2 кг. Знайти: a.

Рис. 1.5.

Розв’язок. Система, що рухається, складається з трьох тіл – двох вантажів і блоку, для яких можна застосувати рівняння руху. Обидва вантажі рухаються поступально, і на кожен діють дві сили: сила ваги і сила натягу нитки. Направивши вісь x вертикально донизу, для кожного вантажу можна записати рівняння руху (рівняння другого закону Ньютона) у проекціях на цю вісь

; (1)

. (2)

Блок обертається під дією моментів сил і щодо осі, перпендикулярної до площини креслення і спрямованої за креслення, у результаті чого він набуває кутове прискорення , обумовлене рівнянням динаміки обертального руху для твердого тіла

, (3)

де J – момент інерції блоку.

Для суцільного диска момент інерції відносно осі, що проходить по осі симетрії, маємо

. (4)

Лінійне прискорення вантажів чисельно дорівнює тангенціальному прискоренню точок на зовнішній поверхні блоку, тому що відсутнє проковзування нитки. Прискорення a і зв’язані співвідношенням

. (5)

Нитки, як видно з умови задачі, можна вважати невагомими. Тому, згідно з третім законом Ньютона, відповідні сили дорівнюють

; (6а)

. (6б)

Підставляючи вирази (4)-(6) у (3), після нескладних перетворень легко одержати

. (7)

Рівняння (1), (2) і (7) являють собою систему, що містить три невідомі величини – прискорення a і сили натягу ниток T₁ і T₂. Для її розв’язку можна, наприклад, замінити знаки на протилежні в (1), а потім скласти між собою відповідно ліві і праві частини всіх рівнянь системи. В результаті легко одержати остаточний вираз для пошукуваного прискорення

. (8)

Обчислення.

= 2,88 м/с².

Відповідь: a = 2,88 м/с².

Приклад 12. Платформа у вигляді суцільного диску радіусом 1,5 м і масою 180 кг обертається біля вертикальної осі з частотою 10 об/хв. У центрі платформи стоїть людина масою 60 кг. Яку лінійну швидкість щодо підлоги приміщення буде мати людина, якщо вона перейде на край платформи?

Дано: m₁ = 180 кг; m₂ = 60 кг; n₁ = 10 об/хв = 1/6 об/с; R = 1,5 м; r = 0.

Знайти: .

Розв’язок. Відповідно до умови задачі момент зовнішніх сил відносно осі обертання, що збігається з геометричною віссю платформи, можна вважати рівним нулю. За цієї умови діє закон збереження моменту імпульсу системи «платформа – людина»

. (1)

Тут L і – відповідно моменти імпульсу системи у вихідному й у кінцевому станах, для яких можна записати такі вирази

; (2)

. (3)

У цих виразах прийнято такі позначення: J₁ і J₂ – моменти інерції платформи і людини у початковому стані; і – у кінцевому стані, відповідно; і – кутова швидкість обертання платформи у початковому й у кінцевому станах.

Кутову швидкість можна виразити через частоту обертання n, а величину пов’язати з пошукуваною кінцевою лінійною швидкістю людини

. (4)

. (5)

Зауважимо, що, відповідно до умови задачі, момент інерції платформи не змінюється, а для моменту інерції людини застосовною, є формула моменту інерції матеріальної точки

; (6)

; (7a)

(7б)

Тепер можна підставити вираження (2) і (3) у (1), використовуючи (4), (6) і (7). В результаті, приймаючи до уваги, що r = 0, а , можна одержати

. (8)

Остаточну формулу одержимо, підставляючи отриманий вираз у вираз (5)

. (9)

Обчислення.

= 1 м/с.

Відповідь: = 1 м/с.

Приклад 13. Стрижень довжиною 1 м рухається повз спостерігача із швидкістю 0,8c (c – швидкість світла у вакуумі). Якою буде довжина цього стрижня в системі відліку, пов’язаної зі спостерігачем?

Дано: l₀ = 1 м; = 0,8c.

Знайти: l.

Розв’язок. Залежність довжини тіла від швидкості в релятивістській механіці виражається формулою

. (1)

Підставляючи у формулу (1) числові значення, одержимо

= 0,6 м.

Відповідь: l = 0,6 м.

Приклад 14. Дві частинки рухаються назустріч одна одній із швидкостями щодо нерухомого спостерігача: 1) ; ; 2)  ; . Знайти їхню відносну швидкість у першому і другому випадках.

Дано: 1) ; u = 0,75c; 2) , u = 0,75c.

Знайти: u^′.

Розв’язок. Закон додавання швидкостей у релятивістській механіці визначається формулою

, (1)

де u – швидкість частинки в базовій інерціальній системі відліку К, – швидкість частинки в інерціальній системі відліку , – швидкість системи щодо системи К. Зважаючи на те, що частинки рухаються на зустріч одна одній, формулу (1) треба записати таким чином

, (2)

звідки відносна швидкість частинок буде визначатись так

. (3)

Зробимо обчислення.

1) .

2) .

Таким чином, 1) ні в одній інерціальній системі відліку швидкість не може бути більшою ніж швидкість світла; 2) швидкість розповсюдження світла у вакуумі абсолютна.

Відповідь: 1). ; 2) .

Приклад 15. Визначити релятивістський імпульс електрона, кінетична енергія якого дорівнює 5 МеВ.

Дано: T = 5 МеВ = 8·10^-13 Дж; m = 9,31·10^-31 кг.

Знайти: p.

Розв’язок. Імпульс релятивістської частки може бути знайдений з виразу

, (1)

де Е – повна енергія частинки; Е₀ – енергія спокою частинки, E₀ =mc² = = 0,51 МеВ = 81·10^-13 Дж.

Різниця Е – Е₀ = Т – кінетична енергія частинки; Е + Е₀ = 2Е₀ + Т, (тому що Е = Е₀ + Т). Це дозволяє пов’язати релятивістський імпульс з кінетичною енергією

. (2)

Тут c – швидкість світла у вакуумі.

Обчислення.

кг·м/с.

Відповідь: p = 2,8·10^-21 кг·м/с.