
- •Передмова
- •Елементи спеціальної (окремої) теорії відносності
- •Основи молекулярної фізики і термодинаміки
- •Електростатика
- •Постійний електричний струм
- •Електромагнетизм
- •Механічні коливання і хвилі в пружних середовищах
- •Електромагнітні коливання і хвилі
- •Хвильова оптика
- •Квантова природа випромінювання
- •Елементи атомної фізики і квантової механіки
- •Елементи квантової статистики і фізики твердого тіла
- •Елементи фізики атомного ядра й елементарних частинок
- •Література
- •Загальні методичні вказівки
- •Відомості про наближені обчислення
- •Навчальні матеріали до розділів курсу фізики
- •1. Фізичні основи механіки Пояснення до робочої програми
- •Основні закони і формули
- •Приклади розв’язку задач
- •Контрольна робота № 1
- •Питання для самоперевірки
- •2. Молекулярна фізика і термодинаміка Пояснення до робочої програми
- •Основні закони і формули
- •Приклади розв’язку задач
- •Контрольна робота № 2
- •Питання для самоперевірки
- •3. Електростатика. Постійний струм Пояснення до робочої програми
- •Основні закони і формули
- •Приклади розв’язку задач
- •Контрольна робота № 3
- •Питання для самоперевірки
- •4. Електромагнетизм. Коливання і хвилі Пояснення до робочої програми
- •Основні закони і формули
- •Приклади розв’язку задач
- •Контрольна робота № 4
- •Питання для самоперевірки
- •5. Квантова оптика. Елементи атомної та ядерної фізики і фізики твердого тіла Пояснення до робочої програми
- •Основні закони і формули
- •Приклади розв’язку задач
- •Контрольна робота № 5
- •Питання для самоперевірки
- •Додатки
- •Одиниці фізичних величин
- •Приставки до одиниць величин
- •Деякі астрономічні величини
- •Основні фізичні константи
- •Густина речовини
- •Ефективний діаметр молекули (м)
- •Питомий опір і температурний коефіцієнт провідників
- •Діелектрична проникність
- •Показник заломлення
- •Маса й енергія спокою деяких елементарних і легких ядер
- •Робота виходу електронів з металу
- •Маси деяких ізотопів (в а.О.М.)
- •Періоди піврозпаду радіоактивних ізотопів
- •Навчальне видання
- •Рудакова Галина Олександрівна
- •Методичні вказівки та
- •Контрольні завдання з фізики
Приклади розв’язку задач
Приклад 1. Два паралельні нескінченно довгі провідники, по яких течуть в одному напрямку електричні струми силою 60 А, розташовані на відстані 10 см один від одного. Визначити магнітну індукцію поля, створеного провідниками зі струмом у точці А, що знаходяться від одного проводу на відстані 5 см, а від іншого – 12 см (рис. 4.1). |
Рис. 4.1. |
Дано: I = 60 A, d = 0.1 м, r 1 =5·10–2 м, r 2 = 12·10–2 м.
Знайти: B.
Розв’язок.
 Відповідно
до принципу суперпозиції магнітна
індукція
Відповідно
до принципу суперпозиції магнітна
індукція
![]() в шуканій точці визначається як векторна
сума магнітних індукцій
в шуканій точці визначається як векторна
сума магнітних індукцій
![]() і
і
![]() полів, створених кожним провідником
окремо.
полів, створених кожним провідником
окремо.
![]() .
Модуль вектора
може бути знайдений з теореми косинусів
.
Модуль вектора
може бути знайдений з теореми косинусів
![]() .
.
У свою чергу В1 і В2 визначаються формулами
![]() ;
;
![]() .
.
Після підстановки цих виразів знайдемо
![]() .
.
Обчислимо
![]() з трикутника АСD,
де кут
з трикутника АСD,
де кут
![]() DAC
=
(як кути, утворені взаємно перпендикулярними
сторонами)
DAC
=
(як кути, утворені взаємно перпендикулярними
сторонами)
![]() .
.
Звідси
![]() .
.
Обчислення.
![]() Тл.
Тл.
Відповідь: B = 3,08·10-4 Тл.
Приклад 2. Ізольований прямолінійний провідник зігнутий під прямим кутом із стороною, довжина якої 20 см. У площині кута поміщений кільцевий провідник радіусом 10 см так, що сторони кута є дотичними до кільцевого (рис. 4.2а). Знайти індукцію у центрі кільця. Сили струмів у провідниках дорівнюють 2 А. |
Рис. 4.2. |
Дано:
l
= 0,2 м, r0
= 0,1 м;
![]() ;
I1
= I2
= I
= 2 A.
;
I1
= I2
= I
= 2 A.
Знайти: В.
Розв’язок.
Магнітна індукція поля в точці М
відповідно до принципу суперпозиції
визначається векторною сумою магнітних
індукцій полів кільцевого і прямолінійного
провідників зі струмом. Індукція в
центрі кільцевого провідника
![]() .
.
Індукція,
створена в точці М відрізком АВ прямого
провідника на відстані r0
від нього дорівнює (рис. 4.2б):
![]() .
.
Цю формулу в деяких випадках зручно записувати у виді
![]() .
.
За
умовою задачі
![]() індукція від двох сторін кута складає
індукція від двох сторін кута складає
![]() .
.
Правило правого гвинта дозволяє встановити, що напрямок векторів індукцій полів В1 і В3, створених провідниками, збігаються, тому результуюча індукція в центрі кільця дорівнює їх алгебраїчній сумі
![]() .
.
Обчислення.
![]() Тл.
Тл.
Відповідь: B = 15,32·10-4 Тл.
Приклад 3. Протон, що пройшов прискорюючу різницю потенціалів 600 В, влетів в однорідне магнітне поле з індукцією 0,3 Тл і почав рухатися по колу. Обчислити радіус кола.
Дано: U = 600 B; B = 0,3 Тл; = 900; m = 1,67·10–27 кг.
Знайти: R.
Розв’язок.
У магнітному полі з індукцією
на заряд, що рухається, діє сила Лоренца
.
Рух заряду буде відбуватися по колу
тільки в тому випадку, коли частинка
влітає у магнітне поле перпендикулярно
лініям магнітної індукції
![]() ,
тобто
,
тобто
![]() .
Тоді
.
Тоді
![]() .
Ця сила перпендикулярна векторові
швидкості і надає частинці доцентрове
прискорення
.
Ця сила перпендикулярна векторові
швидкості і надає частинці доцентрове
прискорення
![]() .
.
Відповідно
до другого закону Ньютона можна записати
![]()
![]() ,
звідки
,
звідки
![]() .
Кінетичну енергію
.
Кінетичну енергію
![]() протон набуває за рахунок роботи сил
електричного поля
протон набуває за рахунок роботи сил
електричного поля
![]() ,
тому
,
тому
![]()
![]() і
і
![]() .
Підставляючи знайдену швидкість
у вираз для радіуса R,
одержимо
.
Підставляючи знайдену швидкість
у вираз для радіуса R,
одержимо
![]() .
.
Обчислення.
![]() м
= 11,8 мм.
м
= 11,8 мм.
Відповідь: R = 11,8 м.
Приклад 4. Коротка котушка, що містить 1000 витків, рівномірно обертається з частотою 10 об/с відносно осі, що лежить у площині котушки і перпендикулярна до ліній однорідного магнітного поля з індукцією 0,04 Тл (рис. 4.3). Визначити миттєве значення ЕРС індукції для тих моментів часу, коли площина котушки складає кут 600 з лініями поля. Площа котушки дорівнює 100 см2. |
Рис. 4.3. |
Дано: N = 103, n = 10 об/с, B = 0,04 Тл, S = 10-2 м2.
Знайти:
![]() .
.
Розв’язок. Миттєве значення ЕРС індукції визначається основним рівнянням електромагнітної індукції Фарадея-Максвелла
![]() .
.
При
обертанні котушки магнітний потік
змінюється за законом
![]() .
Підставляючи вираз магнітного потоку
у формулу для
.
Підставляючи вираз магнітного потоку
у формулу для
![]() і диференціюючи за часом, знайдемо
і диференціюючи за часом, знайдемо
![]() .
.
З
огляду на те, що кутова швидкість
пов’язана з частотою обертання n
і що кут
![]() ,
одержимо
,
одержимо
![]() .
.
Зробимо обчислення.
![]() В.
В.
Відповідь:
![]() В.
В.
Приклад 5. Прямолінійний провідник, довжиною 1,2 м, з’єднаний із джерелом струму, ЕРС якого 24 В и внутрішній опір 0,5 Ом. Провідник знаходиться в однорідному магнітному полі з індукцією 0,8 Тл. Знайти струм у колі, якщо провідник рухається перпендикулярно лініям індукції поля з швидкістю 12,5 м/с. У скільки разів зміниться величина струму в колі, якщо провідник зупиниться? Опір усього зовнішнього кола прийняти за 2,5 Ом. Магнітним полем струму у провіднику знехтувати.
Дано:
l
= 1,2 м;
24 В; r
= 0,5 Ом; R
= 2,5 Ом; B
= 0,8 Тл;
Знайти:
Розв’язок. Сила струму в провіднику визначається ЕРС джерела і різницею потенціалів, що виникає на кінцях провідника при його русі в напрямку, перпендикулярному до ліній магнітної індукції, тобто |
Рис. 4.4. |
![]() .
.
У залежності від напрямку руху провідника може або додавався до джерела, або відніматися. Тоді
![]() А;
А;
![]() А;
А;
![]() А.
А.
Якщо
провідник зупиниться, то
![]() А. Таким чином, при зупинці провідника
струм або збільшується в 2 рази, або
зменшується в 1,5 рази.
А. Таким чином, при зупинці провідника
струм або збільшується в 2 рази, або
зменшується в 1,5 рази.
Приклад 6. Дротяна квадратна рамка із стороною 5 см і опором 10 Ом знаходиться в однорідному магнітному полі з індукцією 40 мТл. Нормаль до площини рамки складає кут 300 з лініями магнітної індукції. Визначити заряд, що пройде по рамці, якщо магнітне поле виключити.
Дано: a = 5·10–2 м, R = 10–2 Ом, В = 4·10–2 Тл, = 300.
Знайти: q.
Розв’язок.
При вимиканні магнітного поля внаслідок
зміни магнітного потоку в рамці наводиться
ЕРС індукції
![]() ,
яка викликає індукційний струм. Відповідно
до закону Ома для повного кола
,
яка викликає індукційний струм. Відповідно
до закону Ома для повного кола
![]() або
або
![]() .
.
З
урахуванням того, що
![]() запишемо
запишемо
![]() .
.
Проінтегрувавши цей вираз, знайдемо
 або
або
![]() .
.
За
умовою задачі Ф2
= 0, а
![]() і S
= a2
,
тому
запишемо
і S
= a2
,
тому
запишемо
![]() .
.
Зробимо обчислення.
![]() Кл.
Кл.
Відповідь: q = 8,67·10-3 Кл.
Приклад 7. Виток радіусом 2 см, по якому тече струм у 10 А, вільно встановився в однорідному магнітному полі з індукцією 1,5 Тл. Лінії індукції перпендикулярні до площини витка. Визначити роботу зовнішніх сил при повороті витка на кут 900 навколо осі, що збігає з діаметром витка.
Дано: I = 10 A; B = 1,5 Тл; r = 0,02 м; = 900.
Знайти: А.
Розв’язок.
На виток зі струмом діє обертовий момент
![]()
![]() ,
де магнітний момент
,
де магнітний момент
![]() .
.
У
початковому положенні, відповідно до
умови задачі, виток вільно установився
в магнітному полі, отже, вектори
![]() і
і
![]() збігаються за напрямками, тобто
збігаються за напрямками, тобто
![]() і М
= 0.
і М
= 0.
При дії зовнішніх сил виток виходить з початкового положення. При цьому зовнішні сили виконують роботу проти цього моменту, що є перемінним і залежить від кута повороту
![]() або
або ![]() .
.
Проінтегрувавши цей вираз, знайдемо роботу, виконану при повороті витка на кінцевий кут
![]() .
.
Зробимо обчислення.
![]() Дж.
Дж.
Відповідь: А = 18,84·10-3 Дж.
Приклад 8. Соленоїд із сердечником з немагнітного матеріалу містить 1200 витків проводу, що щільно прилягають один до одного. При силі струму 4 А магнітний потік дорівнює 6 мкВб. Визначити індуктивність соленоїда і енергію магнітного поля соленоїду.
Дано: N = 1200; I = 4 A; Ф = 6·10–6 Вб.
Знайти: L, Wm.
Розв’язок. Індуктивність пов’язана з потокозчепленням і силою струму співвідношенням
![]() .
.
Враховуючи,
що
![]() ,
то
,
то
![]() .
.
Енергія
магнітного поля соленоїда
![]() .
.
Підставивши вираз для індуктивності, одержимо
![]() .
.
Зробимо обчислення.
![]() Гн
= 1,8 мГн.
Гн
= 1,8 мГн.
![]() Дж
= 14,4 мДж.
Дж
= 14,4 мДж.
Відповідь: L = 1,8·10-3 Гн = 1,8 мГн; Wm = 1,44·10-2 Дж = 14,4 мДж.
Приклад 9. Матеріальна точка масою 10 г виконує коливання з періодом 1 с. Початкова фаза коливань 300. Визначити амплітуду коливань, максимальні швидкість і прискорення точки, що коливається, а також найбільше значення сили, що діє на точку, якщо максимальна кінетична енергія дорівнює 0,02 Дж.
Дано:
m
= 10–2
кг, Т
= 1 с,
![]() ,
Wk
max
= 0,02 Дж.
,
Wk
max
= 0,02 Дж.
Знайти:
А,
![]() ,
amax.
,
amax.
Розв’язок.
Повна енергія точки, що коливається,
дорівнює сумі кінетичної і потенціальної
енергії; вона дорівнює максимальній
кінетичній або максимальній потенційній
енергії. Повна енергія гармонічного
коливання визначається формулою
![]() ,
звідки
,
звідки
![]() .
.
З
огляду на те, що
![]() ,
одержимо
,
одержимо
![]() м.
м.
Запишемо рівняння гармонічних коливань
![]() ,
,
де
А
= 0,32 м,
![]() с–1,
с–1,
![]() .
.
Швидкість
визначається як перша похідна від
зміщення за часом
![]() ,
а
,
а
![]() м/с (з урахуванням того, що
м/с (з урахуванням того, що
![]() ).
).
Прискорення – перша похідна від швидкості за часом
![]() .
.
Припускаючи,
що
![]() ,
знайдемо
,
знайдемо
![]() =
12,62 м/с2.
=
12,62 м/с2.
Частинка
робить гармонічні коливання під дією
квазіпружної сили
![]() ,
де k
– коефіцієнт квазіпружної сили, х
– зміщення точки, що коливається. Сила
буде мати максимальне значення при
зміщенні xmax,
яке дорівнює амплітуді
,
де k
– коефіцієнт квазіпружної сили, х
– зміщення точки, що коливається. Сила
буде мати максимальне значення при
зміщенні xmax,
яке дорівнює амплітуді
![]() .
.
Коефіцієнт k зв’яжемо з періодом коливань
![]() .
.
Тоді
![]() ;
;
![]() Н.
Н.
Відповідь:
![]() м/с;
м/с;
![]() м/с2;
м/с2;
![]() Н.
Н.
Приклад 10. Точки, що коливаються, віддалені від джерела коливань на відстань 1 м і 1,21 м у напрямку поширення хвилі. Різниця фаз коливань /4, частота коливань джерела 200 с–1. Визначити довжину хвилі і швидкість її поширення.
Дано:
х1
= 1 м; х2
= 1,21 м,
![]() ,
=2·102
с–1.
,
=2·102
с–1.
Знайти:
![]() ,
.
,
.
Розв’язок. З рівняння хвилі, що біжить, для коливання в точках х1 і х2 можна записати
![]() ,
,
![]() .
.
Знайдемо
різницю фаз коливань
![]() .
.
З
огляду на те, що
![]() ,
одержимо
,
одержимо
![]() ,
звідки
,
звідки
![]() ;
; ![]() м.
м.
Швидкість поширення хвилі
![]() м/с.
м/с.
Відповідь:
![]() м;
м;
![]() м/с.
м/с.
Приклад
11.
Різниця потенціалів на обкладках
конденсатора в коливальному контурі
змінюється з часом за законом
![]() .
Електроємність конденсатора 0,5 мкФ.
Визначити період власних коливань,
індуктивність, енергію контуру і
максимальну силу струму, що тече в
котушці індуктивності.
.
Електроємність конденсатора 0,5 мкФ.
Визначити період власних коливань,
індуктивність, енергію контуру і
максимальну силу струму, що тече в
котушці індуктивності.
Дано: U = 100sin1000 t; С = 0,5·10–6 Ф.
Знайти: Т, L, W, Imax.
Розв’язок.
Напруга на обкладках конденсатора
змінюється за гармонічним законом
![]() ,
де U0
– амплітудне (максимальне) значення
напруги;
,
де U0
– амплітудне (максимальне) значення
напруги;
![]() – власна циклічна частота коливань, що
пов’язана з періодом коливань
– власна циклічна частота коливань, що
пов’язана з періодом коливань
![]() .
.
Звідси
![]() с.
с.
З
формули Томсона для періоду власних
коливань у контурі знайдемо індуктивність
![]() ,
тому
,
тому
![]() ;
;
![]() Гн = 0,2 Гн.
Гн = 0,2 Гн.
Енергія
контуру – це сума електричної
![]() і магнітної
енергій, і дорівнює максимальній енергії
поля конденсатора
і магнітної
енергій, і дорівнює максимальній енергії
поля конденсатора
![]() або максимальній енергії котушки
індуктивності
або максимальній енергії котушки
індуктивності
![]() .
.
W = 0,5·10-6·1002/2 = 2,5·10-3 Дж.
Знаючи повну енергію, можна визначити максимальну силу струму, що протікає в котушці
![]() ;
;
![]() А.
А.
Відповідь:
T
= 0,002 с;
![]() Гн; W
= 2,5·10-3
Дж; Imax
= 0,15 А.
Гн; W
= 2,5·10-3
Дж; Imax
= 0,15 А.
Приклад 12. Відстань між двома когерентними джерелами 0,9 мм. Джерела посилають монохроматичне світло з довжиною хвилі 640 нм на екран, розташований від них на відстані 3,5 м. Визначити число світлих смуг на 1 см довжини. Дано: d = 9·10–4 м, = 6,4·10–7 м, L = 3,5 м, х = 10–2 м. |
Рис. 4.5. |
Знайти: k/х.
Розв’язок.
У точці О на екрані (рис. 4.5) буде максимальна
освітленість. Ця точка рівновіддалена
від обох джерел S1
і S2,
тому різниця ходу променів S1O
і S2O
дорівнює нулю. У довільній точці О1
максимум освітленості буде спостерігатися,
якщо різниця ходу променів дорівнює
цілому числу довжин хвиль
![]() ,
де k
– номер світлої смуги. З рисунка видно,
що
,
де k
– номер світлої смуги. З рисунка видно,
що
![]() ,
звідки
,
звідки
![]() і тому
і тому
![]() .
Звідси число світлих інтерференційних
смуг, що припадають на одиницю довжини
.
Звідси число світлих інтерференційних
смуг, що припадають на одиницю довжини
![]() .
.
Підставляючи числові дані, одержимо
![]() м-1.=
4 см-1.
м-1.=
4 см-1.
Відповідь:
![]() см-1.
см-1.
Приклад 13. На скляний клин нормально до його грані падає монохроматичне світло з довжиною хвилі 0,6 мкм. Число інтерференційних смуг, що припадає на 1 см, дорівнює 10. Визначити заломлюючий кут клина (n = 1,5). |
Рис. 4.6. |
Дано: n = 1,5; i = 00; = 6·10–7 м; l = 10–2 м; N = 10.
Знайти: .
Розв’язок. Паралельний пучок променів, падаючи нормально до грані клина, відбивається як від верхньої, так і від нижньої граней. Ці промені когерентні і тому спостерігається стійка інтерференційна картина при їхньому накладенні. Різниця ходу променів визначається формулою
![]() . (1)
. (1)
Темні смуги спостерігаються на тих ділянках клина, для яких різниця променів кратна непарному числу напівхвиль
![]() . (2)
. (2)
Дорівнявши праві частини рівнянь (1) і (2) одержимо
![]() .
.
Оскільки
кут падіння i
= 0 (sini
= 0), то
![]() ,
звідки
,
звідки
![]() ,
де dk
– товщина клина в тому місці, де
спостерігається темна смуга, що відповідає
номеру k.
Сусідня темна смуга з номером (k
+ 1), що відповідає товщині клина dk+1
, знаходиться на відстані l/N.
(рис. 4.6),
,
де dk
– товщина клина в тому місці, де
спостерігається темна смуга, що відповідає
номеру k.
Сусідня темна смуга з номером (k
+ 1), що відповідає товщині клина dk+1
, знаходиться на відстані l/N.
(рис. 4.6),
![]() .
.
На
рисунку бачимо, що пошукуваний кут
(через його малість, можна вважати
![]() )
)
![]() ,
або
,
або
![]() .
.
Підставивши числові дані, одержимо
![]() рад.;
рад.; ![]() .
.
Відповідь: .
Приклад 14. На дифракційну ґратку нормально падає паралельний пучок променів з довжиною хвилі 500 нм. На екрані, паралельному дифракційній ґратці і віддаленому від неї на 1 м, спостерігається дифракційна картина. Відстань між максимуму першого порядку на екрані дорівнює 20,2 см. Визначити сталу дифракційної ґратки, число штрихів на 1 см, число максимумів, що дає дифракційна ґратка, макси- |
|
мальний кут відхилення променів, що відповідає останньому дифракційному максимуму.
Дано: λ = 5·10–7 м, L = 1 м, k = 1, l = 0,202 м.
Знайти: d, N, kmax, .
Розв’язок.
Умова максимуму при дифракції від ґратки
має вид
![]() .
У цій задачі порядок спектра k
= 1, а
.
У цій задачі порядок спектра k
= 1, а
![]() (зазначене наближення має місце, тому
що
(зазначене наближення має місце, тому
що
![]() ).
Тоді
).
Тоді
![]() ,
звідки стала ґратки
,
звідки стала ґратки
![]() .
Підставивши числові дані, одержимо
.
Підставивши числові дані, одержимо
![]() м.
м.
Число штрихів на одиниці довжини знайдемо з формули
![]() м-1
= 2020 см-1.
м-1
= 2020 см-1.
Для визначення числа максимумів, яке дає дифракційна ґратка, обчислимо максимальне значення k, яке визначимо з тієї умови, що максимальний кут відхилення променів дифракційними ґратками не може перевищувати 900.
![]() .
.
Оскільки
число максимумів k
повинно бути тільки цілим числом, то k
= 9 (k
не може прийняти значення 10, тому що при
цьому
![]() ).
).
Підрахуємо число максимумів, яке дає дифракційна ґратка: вліво і вправо від центрального максимуму, для котрого k = 0, буде спостерігатися однакове число максимумів, що дорівнює kmax, тобто всього 2kmax. З огляду на центральний (нульовий) максимум, одержимо загальне число максимумів M = 2kmax + 1, тобто M = 2·9+1 = 19.
Найбільший кут відхилення променів, що відповідає останньому дифракційному максимуму знайдемо у такий спосіб
![]() ,
тобто
,
тобто
![]()
Відповідь:
d
= 4,95·10-6
м; N
= 2020 см-1;
![]() ;
;
Приклад 15. Природне світло падає на поліровану поверхню скляної пластини, зануреної в рідину. Відбитий від пластини промінь утворює кут 970 з падаючим променем. Визначити показник заломлення рідини, якщо відбитий промінь максимально поляризований.
Дано: iб = 970/2; n2 = 1,5.
Знайти: n1.
Розв’язок.
Відповідно до закону Брюстера відбитий
промінь буде максимально поляризований,
якщо тангенс кута падіння чисельно
дорівнює відносному показникові
заломлення;
![]() ,
звідки
,
звідки
![]() .
.
![]() .
.
Відповідь: n1 = 1,33.
Приклад 16. Який кут утворюють площини поляризації двох ніколей, якщо світло, що вийшло з другого ніколя, було ослаблене у 5 разів. Врахувати, що поляризатор поглинає 10 %, а аналізатор 8 % падаючого на них світла.
Дано: k1 = 0,1; k2 = 0,08; n = I0/I2 = 5.
Знайти:
![]()
Розв’язок.
Природний промінь світла, падаючи на
грань призми Ніколя, зазнає подвійного
променезаломлення, у результаті чого
виникають два промені: звичайний і
незвичайний. Обидва промені поляризовані
у взаємно перпендикулярних площинах,
інтенсивність їх однакова і дорівнює
половині інтенсивності природного
світла. З урахуванням поглинання
інтенсивність світла, що пройшло через
поляризатор
![]()
![]() ,
де I0
–
інтенсивність природного світла, що
падає на перший ніколь.
,
де I0
–
інтенсивність природного світла, що
падає на перший ніколь.
Поляризований
промінь, потрапляючи на другу призму
(аналізатор), знову випробує поглинання.
Крім того, інтенсивність цього променя
зменшується через розбіжність площин
поляризації поляризатора й аналізатора.
Зменшення інтенсивності визначається
законом Молюса
![]() .
.
З урахуванням втрат інтенсивності світла в аналізаторі, одержимо
![]() ,
,
звідки
![]() .
.
Зробимо обчислення.
![]() ,
тобто
,
тобто
![]() .
.
Відповідь: .

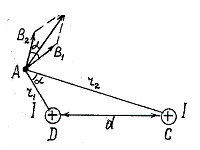
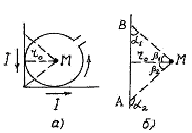
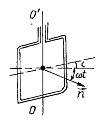
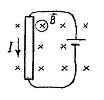


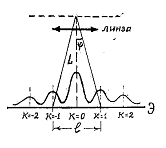 Рис.
4.7.
Рис.
4.7.