
- •Передмова
- •Елементи спеціальної (окремої) теорії відносності
- •Основи молекулярної фізики і термодинаміки
- •Електростатика
- •Постійний електричний струм
- •Електромагнетизм
- •Механічні коливання і хвилі в пружних середовищах
- •Електромагнітні коливання і хвилі
- •Хвильова оптика
- •Квантова природа випромінювання
- •Елементи атомної фізики і квантової механіки
- •Елементи квантової статистики і фізики твердого тіла
- •Елементи фізики атомного ядра й елементарних частинок
- •Література
- •Загальні методичні вказівки
- •Відомості про наближені обчислення
- •Навчальні матеріали до розділів курсу фізики
- •1. Фізичні основи механіки Пояснення до робочої програми
- •Основні закони і формули
- •Приклади розв’язку задач
- •Контрольна робота № 1
- •Питання для самоперевірки
- •2. Молекулярна фізика і термодинаміка Пояснення до робочої програми
- •Основні закони і формули
- •Приклади розв’язку задач
- •Контрольна робота № 2
- •Питання для самоперевірки
- •3. Електростатика. Постійний струм Пояснення до робочої програми
- •Основні закони і формули
- •Приклади розв’язку задач
- •Контрольна робота № 3
- •Питання для самоперевірки
- •4. Електромагнетизм. Коливання і хвилі Пояснення до робочої програми
- •Основні закони і формули
- •Приклади розв’язку задач
- •Контрольна робота № 4
- •Питання для самоперевірки
- •5. Квантова оптика. Елементи атомної та ядерної фізики і фізики твердого тіла Пояснення до робочої програми
- •Основні закони і формули
- •Приклади розв’язку задач
- •Контрольна робота № 5
- •Питання для самоперевірки
- •Додатки
- •Одиниці фізичних величин
- •Приставки до одиниць величин
- •Деякі астрономічні величини
- •Основні фізичні константи
- •Густина речовини
- •Ефективний діаметр молекули (м)
- •Питомий опір і температурний коефіцієнт провідників
- •Діелектрична проникність
- •Показник заломлення
- •Маса й енергія спокою деяких елементарних і легких ядер
- •Робота виходу електронів з металу
- •Маси деяких ізотопів (в а.О.М.)
- •Періоди піврозпаду радіоактивних ізотопів
- •Навчальне видання
- •Рудакова Галина Олександрівна
- •Методичні вказівки та
- •Контрольні завдання з фізики
Приклади розв’язку задач
Приклад 1. Визначити число молекул, що містяться в 1 см3 води, і масу молекули води. Виходячи з того, що молекули води мають вигляд кульок, що стикаються одна з одною, знайти діаметр молекул.
Дано:
V
= 10-6
м3,
18·10-3
кг/моль,
![]() 103
кг/м3.
103
кг/м3.
Знайти: N, m1, d.
Розв’язок. Спочатку, користуючись таблицями фізичних величин, знайдемо густину, а потім і молярну масу води. Молярна маса пов’язана з відносною молекулярною масою речовини Mr формулою
![]() кг/моль. (1)
кг/моль. (1)
Відносна молекулярна маса речовини дорівнює сумі відносних атомних мас всіх елементів, атоми яких входять до складу молекули даної речовини, і визначається формулою
![]() , (2)
, (2)
де Ar,i – відносна атомна маса i-го елемента, а ni – число атомів i-го елемента, що входять у молекулу.
Хімічна формула води має вигляд H2O. Звідси випливає, що до складу даної молекули входять два атоми водню (n1 = 2) і один атом кисню (n2 = 1). Значення відносних атомних мас водню і кисню знайдемо з таблиці Д.І. Менделєєва: Ar,1 = 1; Ar,2 = 16.
Таким чином, з (1) і (2) для води маємо
= (n1Ar,1 + n2Ar,2)·10-3 = (2·1 + 1·16)·10-3 = 18·10-3 кг/моль.
Відповідно
до визначення, кількість однорідної
речовини
![]() даної маси m
дорівнює
даної маси m
дорівнює
![]() , (3)
, (3)
де NA – число Авогадро.
Виразивши
масу як добуток густини
![]() на об’єм V,
з виразу (3) одержимо
на об’єм V,
з виразу (3) одержимо
![]() . (4)
. (4)
Масу однієї молекули легко знайти, поділивши молярну масу на число Авогадро
![]() . (5)
. (5)
Для визначення діаметру молекули води приблизно будемо вважати, що в рідині молекули мають форму кульок, що щільно прилягають одна до одної. Згідно з цими уявленнями на кожну молекулу приходиться об’єм V1, що дорівнює об’єму кубічного осередку зі стороною d
V1 = d3. (6)
З іншого боку, об’єм V1 можна знайти, розділивши повний об’єм на число молекул
![]() . (7)
. (7)
Таким чином, підставляючи вираз (7) у (6) і використовуючи (4), можна одержати
![]() . (8)
. (8)
Обчислення.
![]() =
3,34·1019;
=
3,34·1019;
![]() =
2,99·10-26
кг;
=
2,99·10-26
кг;
![]() м.
м.
Відповідь: N =3,34·1019 молекул; m1 =2,99·10-26 кг; d = 3,11·10-10 м.
Приклад 2. У посудині об’ємом 2 м3 знаходиться суміш 4 кг гелію і 2 кг водню при температурі 27 0С. Визначити тиск і молярну масу суміші газів.
Дано:
V
= 2 м3;
m1
= 4 кг; m2
= 2 кг;
![]() 4·10-3
кг/моль;
4·10-3
кг/моль;
![]() =
=
![]() кг/моль; T
= 300 К.
кг/моль; T
= 300 К.
Знайти: p; .
Розв’язок. За законом Дальтона тиск суміші газів дорівнює сумі парціальних тисків газів p1 і p2, що входять до складу суміші
p = p1 +p2. (1)
Фізичні умови, при яких знаходиться суміш газів, не екстремальні, тому в цій задачі застосовано рівняння Клапейрона-Менделєєва
![]() . (2)
. (2)
Застосовуючи це рівняння до гелію і водню, знайдемо їхні парціальні тиски p1 і p2
![]() ; (3а)
; (3а)
![]() . (3б)
. (3б)
Підставляючи вираз (3) у (1), знайдемо тиск суміші
![]() . (4)
. (4)
Молярну масу суміші знайдемо як відношення сумарної маси m до сумарної кількості речовини суміші
![]() . (5)
. (5)
Тут
m = m1 + m2; (6а)
![]() , (6б)
, (6б)
де
![]() і
і
![]() – число молей гелію і водню, які
визначаються відповідно формулами
– число молей гелію і водню, які
визначаються відповідно формулами
![]() ; (7а)
; (7а)
![]() . (7б)
. (7б)
Підставляючи в (5) вираз (6) і (7), одержимо остаточно
![]() . (8)
. (8)
Обчислення.
![]() =
24,9105
Па;
=
24,9105
Па;
 =
3·10-3
кг/моль.
=
3·10-3
кг/моль.
Відповідь: p = 24,9·105 Па; = 3·10-3 кг/моль.
Приклад 3. У балоні об’ємом 10 л знаходиться гелій під тиском 1 МПа і при температурі 300 К. Після того, як з балону було взято 10 г гелію, температура в балоні знизилася до 290 К. Визначити тиск гелію, що залишився у балоні.
Дано:
V
= 10-2
м3;
p1
= 106
Па; T1
= 300 К; T2
= 290 К;![]() m
= 10-2
кг;
=
4·10-3
кг/моль.
m
= 10-2
кг;
=
4·10-3
кг/моль.
Знайти: p2.
Розв’язок. Маса газу, що вийшов з балона, мабуть, дорівнюватиме
m = m1 – m2, (1)
де m1 і m2 – відповідно початкова і кінцева маси гелію в балоні.
З рівняння Менделєєва-Клапейрона для вихідного стану знайдемо первісну масу газу m1, а для кінцевого стану – пошукуваний тиск p2
![]() . (2)
. (2)
![]() . (3)
. (3)
Тепер можна виразити m2 з виразів (1) і (2) і підставити результат у вираз (3)
![]() . (4)
. (4)
Обчислення.
![]() =
3,64·105
Па.
=
3,64·105
Па.
Відповідь: p2 = 3,64·105 Па.
Приклад 4. Знайти середню кінетичну енергію обертального руху однієї молекули кисню при температурі 350 К, а також кінетичну енергію обертального руху всіх молекул кисню масою 4 г.
Дано: T = 350 К; m = 4·10-3 кг, = 32·10-3 кг/моль.
Знайти:
![]() ;
;
![]() .
.
Розв’язок. Середня енергія обертального руху молекул визначається виразом
![]() , (1)
, (1)
де k – стала Больцмана, а іоб – число обертальних ступенів вільності молекули.
Обертальному рухові двохатомної молекули відповідають два ступені вільності. Таким чином, для даної задачі іоб = 2.
Кінетична енергія обертального руху всіх молекул газу очевидно дорівнює добуткові числа молекул N на їхню середню енергію обертального руху
![]() . (2)
. (2)
Число всіх молекул газу можна знайти, використовуючи вираз
![]() . (3)
. (3)
Підставляючи (1) і (3) у (2), одержимо для Eоб такий вираз
![]() . (4)
. (4)
Обчислення.
![]() Дж;
Дж;
![]() Дж.
Дж.
Відповідь: εоб = 4,63·10-21 Дж; Eоб = 364 Дж.
Приклад 5. Кисень масою 2 кг займає об’єм 1 м3 і знаходиться під тиском 0,2 МПа. Газ було нагріто до об’єму 3 м3, а потім при сталому об’ємі до тиску 0,5 МПа. Знайти зміну внутрішньої енергії газу, виконану ним роботу і теплоту, передану газу. Побудувати графік процесу.
Дано: m = 2 кг; 32·10-3 кг/моль; V1 = 1 м3; V2 = V3=3 м3; p1 = p2 = 2·105 Па; p3 = 5·105 Па.
Знайти: U; A; Q.
Розв’язок. З умови задачі випливає, що зміна термодинамічних параметрів системи відбувається у два етапи. Повну зміну внутрішньої енергії газу можна визначити з виразу:
Тут
|
|
умов i = 5, тому що в тепловому русі беруть участь 3 ступені свободи поступального руху і 2 ступені свободи обертального руху, а коливальний рух практично відсутній.
Початкову і кінцеву температуру газу можна знайти з рівняння Менделєєва-Клапейрона
![]() ; (2а)
; (2а)
![]() ; (2б)
; (2б)
![]() . (2в)
. (2в)
Відповідно до умови, на першому етапі газ одночасно розширюється і нагрівається, а на другому – тільки нагрівається. Робота розширення газу при постійному тиску (на першому етапі) виражається формулою
![]() . (3)
. (3)
На другому етапі робота розширення дорівнює нулю, тому що V2 = V3. Таким чином, повна робота, виконана газом, дорівнює роботі, здійсненої ним на першому етапі, тобто A13 = A12.
Теплота, що передана газу, відповідно до першого закону термодинаміки, дорівнює сумі змін внутрішньої енергії і роботи
Q = U + A. (4)
Обчислення.
![]() =
385 К;
=
385 К;
![]() =
1155 К;
=
1155 К;
![]() =
2887 К;
=
2887 К;
![]() =
3,24·106
Дж;
=
3,24·106
Дж;
![]() =
4·105
Дж;
=
4·105
Дж;
Q = 3,24·106 +4·105 Дж = 3,64·106 Дж.
Відповідь:
![]() 3,24·106
Дж; A
= 4·105
Дж; Q
= 3,64·106
Дж. Графік процесу представлений на
рис. 2.1.
3,24·106
Дж; A
= 4·105
Дж; Q
= 3,64·106
Дж. Графік процесу представлений на
рис. 2.1.
Приклад 6. Об’єм аргону, що знаходиться під тиском 80 кПа, збільшився від 1 л до 2 л. На скільки зміниться внутрішня енергія газу, якщо розширення відбувалося: а) ізобарно; б) адіабатно?
Дано: V1 = 1·10-3 м3; V2 = 2·10-3 м3; p = 8·104 Па; = 40·10-3 кг/моль; i = 3.
Знайти:
![]() ;
;
![]() .
.
Розв’язок. Зміна внутрішньої енергії визначається формулою
![]() .
(1)
.
(1)
а) Ізобарний процес. Запишемо рівняння Менделєєва-Клапейрона для початкового і кінцевого станів газу
![]() ; (2а)
; (2а)
![]() . (2б)
. (2б)
Віднімемо з другого виразу перше
![]() . (3)
. (3)
З виразів (1) і (3) легко одержати остаточну формулу для цього випадку
![]() . (4)
. (4)
Обчислення.
![]() =
121 Дж.
=
121 Дж.
б) Адіабатичний процес. Робота при адіабатичному процесі виражається формулою
 або
або
 . (5)
. (5)
Тут
![]() – показник адіабати. Для ідеального
газу його можна визначити з виразу
– показник адіабати. Для ідеального
газу його можна визначити з виразу
![]() . (6)
. (6)
Адіабатичний
процес протікає без теплообміну з
навколишнім середовищем, тому робота
відбувається за рахунок внутрішньої
енергії, тобто Q
= 0, а
![]() .
Таким чином, у даному процесі зміну
внутрішньої енергії можна знайти з
виразу
.
Таким чином, у даному процесі зміну
внутрішньої енергії можна знайти з
виразу
 . (7)
. (7)
Обчислення.
![]() =
1,67;
=
1,67;
 =
–44,6 Дж.
=
–44,6 Дж.
Відповідь: = 121 Дж; = –44,6 Дж.
Приклад 7. Теплова машина працює за циклом Карно. Машина за цикл одержує від нагрівача 1 кДж теплоти і виконує роботу, що дорівнює 350 Дж. Температура нагрівача 500 К. Знайти ККД циклу, температуру холодильника і кількість теплоти, що віддається холодильнику.
Дано: T1 = 500 К; А = 350 Дж; Q1 = 1000 Дж.
Знайти:
![]() ;
T2;
Q2.
;
T2;
Q2.
Розв’язок. ККД циклу теплової машини визначається формулою
![]() . (1)
. (1)
З іншого боку, ККД циклу Карно дорівнює
![]() . (2)
. (2)
Оскільки
теплова машина працює за циклом Карно,
формули (1) і (2) визначають той самий ККД
(![]() ).
Тоді з (2) виходить, що
).
Тоді з (2) виходить, що
![]() . (3)
. (3)
Кількість теплоти, віддану холодильнику, знайдемо з виразу
![]() . (4)
. (4)
Обчислення.
![]() ;
;
T2 = (1 – 0,35)500 = 325 К;
Q2 = 1000 – 350 = 650 Дж.
Відповідь: = 0,35; T2 = 325 К; Q2 = 650 Дж.
Приклад 8. Знайти зміну ентропії при переході 6 г водню від об’єму 20 л під тиском 150 кПа до об’єму 60 л під тиском 100 кПа.
Дано: = 2·10-3 кг/моль; m =6·10-3 кг; p1 = 1,5·105 Па; V1 = =2·10-2 м3; p2 = 105 Па; V2 = 6·10-2 м3; i = 5.
Знайти:
![]() .
.
Розв’язок. Зміна ентропії термодинамічної системи визначається виразом
![]() . (1)
. (1)
Тут dQ – приріст кількості теплоти, для якого перший закон термодинаміки можна записати в диференціальній формі
![]() , (2)
, (2)
де CV – молярна теплоємність газу при постійному об’ємі
![]() . (3)
. (3)
Використовуючи рівняння Менделєєва-Клапейрона, температуру можна виразити через інші термодинамічні параметри
![]() . (4)
. (4)
Звідси знайдемо диференціал
![]() . (5)
. (5)
Після підстановки виразу (5) у (2), а потім у (1), одержимо
 . (6)
. (6)
Остаточно, підставляючи (3) у (6), одержимо:
![]() . (7)
. (7)
Обчислення.
 =
71 Дж/К.
=
71 Дж/К.
Відповідь: = 71 Дж/К.
Приклад 9. Визначити середню довжину вільного пробігу молекул і число зіткнень за 1 с, що відбуваються між усіма молекулами кисню, що знаходиться у посудині об’ємом 2 л при температурі 27 0С и тиску 100 кПа.
Дано: V = 2·10-3 м3; = 32·10-3 кг/моль; Т = 300 К; p = 105 Па; d = 2,9·10-10 м.
Знайти:
![]() ;
Z.
;
Z.
Розв’язок. Середня довжина вільного пробігу молекул обчислюється за формулою
![]() . (1)
. (1)
Тут d – ефективний діаметр молекули, а n – концентрація молекул, яку можна визначити з рівняння p = nkТ, звідки
![]() , (2)
, (2)
де k – стала Больцмана.
Визначаючи концентрацію з формули (2) і, підставляючи її в (1), знайдемо
![]() . (3)
. (3)
Число зіткнень, випробовуваних однією молекулою за 1 с, дорівнює
![]() , (4)
, (4)
де
![]() – середня арифметична швидкість руху
молекул
– середня арифметична швидкість руху
молекул
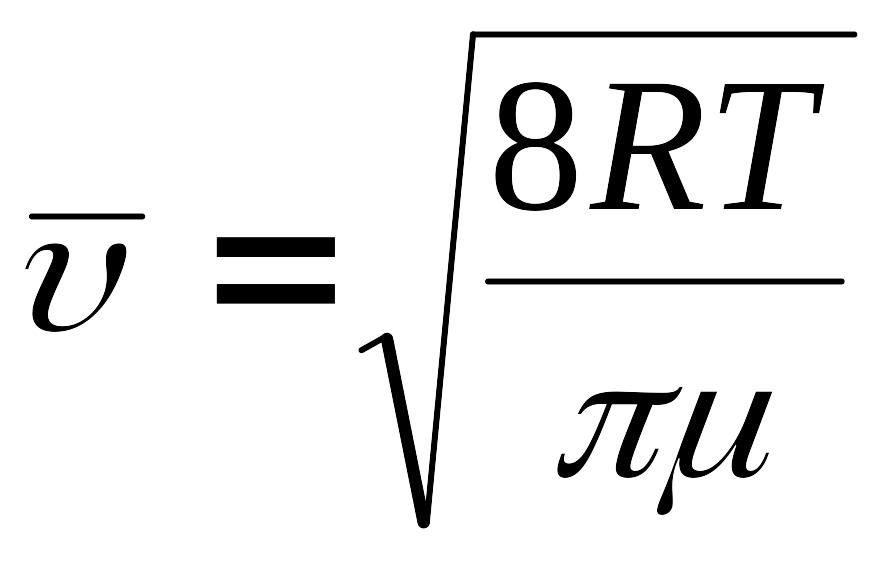 . (5)
. (5)
Кількість молекул у посудині N дорівнює
![]() . (6)
. (6)
Число зіткнень Z, що відбуваються між усіма молекулами за 1 c, дорівнює
![]() , (7)
, (7)
де коефіцієнт 1/2 застосовується для того, щоб зіткнення кожної пари молекул враховувати тільки один раз.
Таким чином, підставляючи вираз (4)–(6) у (7), попередньо визначаючи концентрацію молекул з виразу (2), знайдемо остаточно
![]() . (8)
. (8)
Обчислення.
![]() =
3,56·10-8
м;
=
3,56·10-8
м;
![]() =
9·1028
c-1.
=
9·1028
c-1.
Відповідь:
![]() 3,56·10-8
м; Z
= 9·1028
c-1.
3,56·10-8
м; Z
= 9·1028
c-1.
Приклад 10. Знайти додатковий тиск усередині мильної бульбашки діаметром 10 cм. Яку роботу потрібно виконати, щоб видути цю бульбашку?
Дано:
d
= 0,1 м;
![]() = 4·10-2
Н/м.
= 4·10-2
Н/м.
Знайти:
![]() ;
A.
;
A.
Розв’язок. Плівка мильної бульбашки має дві сферичні поверхні: зовнішню і внутрішню. Обидві поверхні натискають на повітря, що міститься всередині бульбашки. Оскільки товщина плівки надзвичайно мала, то діаметри обох поверхонь практично однакові. Тому додатковий тиск дорівнює
![]() , (1)
, (1)
де
– коефіцієнт поверхневого натягу;
![]() – тиск, створюваний усередині сферичної
поверхні;
– тиск, створюваний усередині сферичної
поверхні;
![]() – радіус мильної бульбашки.
– радіус мильної бульбашки.
Таким чином, додатковий тиск можна знайти з виразу
![]() . (2)
. (2)
Робота,
яку потрібно зробити, щоб, розтягуючи
плівку, збільшити її поверхню на
![]() ,
виражається формулою
,
виражається формулою
![]() , (3)
, (3)
де S – загальна площа двох сферичних поверхонь плівки мильної бульбашки; S0 – загальна площа двох поверхонь плоскої плівки, що затягує отвір трубки до видування бульбашки.
Нехтуючи S0, одержуємо
![]() . (4)
. (4)
Обчислення.
![]() Па;
Па;
A = 2·3,14·0,12·40·10-3 = 2,5·10-3 Дж.
Відповідь: = 3,2 Па; A = 2,5·10-3 Дж.

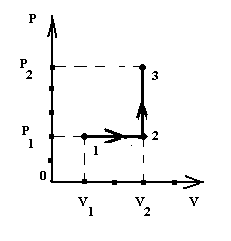 Рис.
2.1.
Рис.
2.1.