4.2 Статические и динамические характеристики сау

Статические режимы САУ характеризуются установившимися состояниями при неизменных входных воздействиях. Уравнения статики легко получить из уравнений динамики САУ путем приравнивания в них нулю всех производных по времени переменных (координат состояния) и внешних воздействий. В операторных уравнениях и на структурных схемах (см. гл. 5) линейных САУ это эквивалентно нулевой частоте изменения переменных, что достигается приравниванием нулю оператора p.

Таким образом, статическая характеристика системы – это зависимость выходной переменной от какой-либо входной переменной в статическом (установившемся) режиме.

Примером статической характеристики является механическая характеристика двигателя постоянного тока (ДПТ) – зависимость угловой частоты вращения вала двигателя от момента нагрузки на валу в установившихся режимах (рис. 4.1). Как видим, при увеличении нагрузки на валу двигателя скорость вращения вала двигателя падает и появляется статическая ошибка регулирования скорости. При изменении нагрузки от нуля до номинального значения M_сн скорость вращения уменьшается от скорости холостого хода до номинальной скорости .

В номинальном режиме статическая ошибка регулирования скорости вращения

. (4.1)

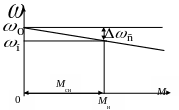
Рис. 4.1 Статическая механическая

характеристика ДПТ

Найдем выражения для установившейся ошибки регулирования при изменении задающих или возмущающих воздействий линейной системы управления.

Передаточная функция любой замкнутой линейной САУ с отрицательной обратной связью (рис. 4.2) определяется передаточными функциями прямого и обратного каналов регулирования (см. гл. 5.3)

. (4.2)

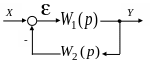
Рис. 4.2 Структурная схема

замкнутой САУ

Отсюда изображение ошибки регулирования в системе

, (4.3)

а передаточная функция по ошибке

. (4.4)

Как следует из (4.3), ошибка регулирования будет стремиться к нулю при X = const, если , что предполагает реализацию бесконечно большого усиления в устройстве управления и может привести к неустойчивости системы. Кроме того, реальные динамические звенья обладают конечными коэффициентами усиления, что приводит к возникновению ненулевой статической ошибки регулирования.

Между тем, статическая ошибка регулирования в системе при неизменном входном воздействии может быть сведена к нулю, если сделать равной нулю передаточную функцию ошибки по задающему или возмущающему воздействию при p=0. Для этого достаточно в прямой или обратный канал регулирования системы, приведенной два рис. 4.2, ввести интегрирующее звено. На практике интегрирующее звено вводят в структуру устройства управления, применяя И-, ПИ-, ПИД-регуляторы. Это обеспечивает и, тем самым нулевую статическую ошибку регулирования. Такие системы принято называть астатическими первого порядка по задающему или (и) возмущающему воздействию. Для придания системе астатизма более высокого порядка в структуру регулятора вводят соответствующее число интеграторов.

Величина установившейся ошибки регулирования, наличие и порядок астатизма замкнутой САУ определяются не только ее моделью, но и видом входного сигнала. Определим, как вид входного воздействия влияет на величину установившейся ошибки.

Передаточную функцию прямого канала запишем в виде

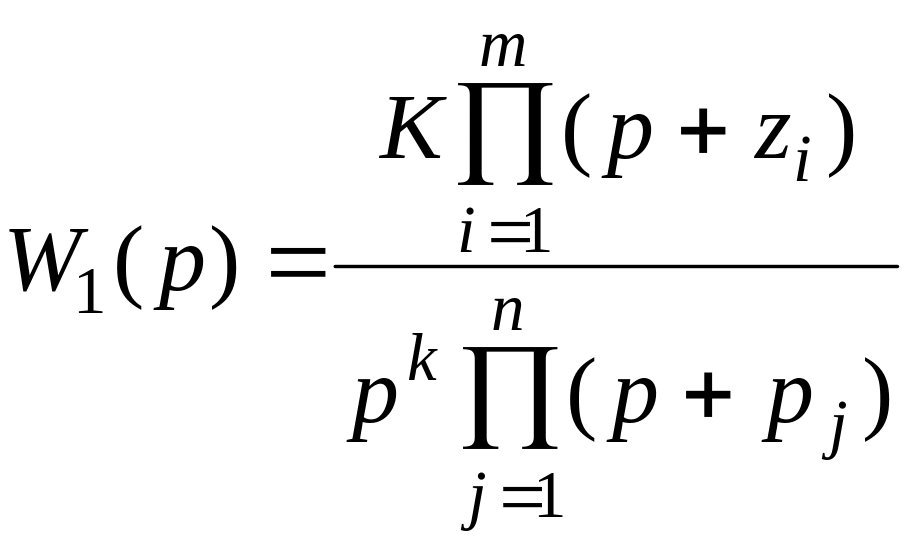, (4.5)

где K – коэффициент передачи,

z_i, p_j – полюсы и нули передаточной функции (4.5).

Для определения величины установившейся ошибки рассмотрим случай единичной обратной связи, т. е. =1.

В установившихся режимах (при p = 0) передаточную функцию (4.4) можно записать в виде

, (4.6)

где K_i – коэффициент ошибки системы, определяемый видом входного воздействия, i = 0, 1, 2.

Поскольку в качестве типовых тестовых сигналов применяют ступенчатое, линейное и квадратичное входное воздействие, то для оценки установившихся ошибок в системе выделяют 3 типа коэффициентов ошибок:

1) коэффициент ошибки по положению (i = 0)

; (4.7)

2) коэффициент ошибки по скорости (i = 1)

; (4.8)

3) коэффициент ошибки по ускорению (i = 2)

. (4.9)

Как следует из выражений (4.3)…(4.9), установившиеся ошибки САУ могут иметь нулевое, бесконечное или постоянное значение в зависимости от числа интеграторов в передаточной функции W₁(p) и типа входного сигнала. Установившиеся ошибки для трех типов входных воздействий и трех типов передаточной функции W₁(p) – с отсутствием интеграторов, с одним и двумя интеграторами – приведены в табл. 4.1.

Таблица 4.1

Установившиеся ошибки САУ при различном числе интеграторов разомкнутого контура

и типах входного воздействия

Число интеграторов	Входной сигнал
	Ступенчатый	Линейный	Квадратичный
0
1
2

Динамические режимы САУ характеризуются переходными состояниями системы при изменении входных (задающих и возмущающих) воздействий. При этом различают свободные и вынужденные переходные процессы.

Назовем процесс вынужденным, если промежуток времени между моментом t_з (t_в) приложения задающего (возмущающего) воздействия X(t) и моментом наблюдения выходной величины Y(t) равен бесконечности. В дальнейшем будем полагать моменты времени приложения воздействий равными нулю. Тогда процесс изменения выходной величины Y(t) в соответствие с теоремой свертывания (умножения изображений) будет иметь вид [1, 2]

, (4.10) где - импульсная переходная функция по внешнему (задающему или возмущающему) воздействию.

Свободный (собственный) процесс в системе определяется решением однородного дифференциального уравнения, описывающего САУ. Он протекает под действием ненулевых начальных условий Y(t₀) и в устойчивых системах асимптотически затухает:

, (4.11)

где – матрица перехода системы из начального состояния Y(t₀) в текущее состояние Y(t). Понятие и расчет матрицы перехода рассмотрены в гл. 9.3.

Полное решение уравнения движения линейных САУ представляет собой сумму решений уравнений свободного и вынужденного движений.

В качестве примера на рис. 4.3 приведена реакция электродвигателя постоянного тока (полное решение уравнения движения) на ступенчатое приложение номинальной нагрузки M_сн (возмущающего воздействия) к его валу.

При приложении нагрузки скорость двигателя падает, причем имеет место колебательный процесс. Максимальный динамический провал скорости превышает статическое падение скорости (см. рис. 4.1).

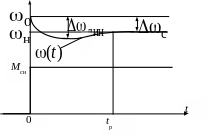
Рис. 4.3 Реакция электродвигателя

на возмущающее воздействие

в виде ступени нагрузки на валу

Вынужденное движение соответствует новому установившемуся состоянию - номинальной скорости электродвигателя. Время переходного процесса (перехода в новое установившееся состояние) составляет t_р .