11.3.2 Метод переменного коэффициента усиления

В основе метода лежат теорема об n интервалах дискретного управления и применение дискретных уравнений переходных состояний [4]. Дискретный регулятор на начальном этапе синтеза представляется в виде последовательной цепочки, состоящей из квантователя ошибки e(t) регулирования по времени с тактом T, фиксатора Ф нулевого порядка и безынерционного звена с переменным коэффициентом К_j усиления (рис. 11.5).

Рис. 11.5 Структура дискретного регулятора на начальном

этапе синтеза

Входным воздействием регулятора является ошибка регулирования e(kT), выходным – сигнал управления u(kT). Ошибка регулирования e(kT) на входе звена с переменным коэффициентом усиления обновляется и фиксируется с помощью экстраполятора нулевого порядка с каждым тактом дискретизации Т.

В соответствие с теоремой об n интервалах дискретного управления система будет оптимальной по быстродействию (в концепции импульсных САУ), если переходные процессы в ней заканчиваются через n тактов управления, причем без перерегулирования выходной координаты, где n - порядок линейного объекта управления. Критерий оптимальности системы (максимум быстродействия) в этом случае записывается в виде t_рег = nT min. Цель синтеза – определение n значений коэффициента К_j, обеспечивающих достижение предельного быстродействия САУ.

Для дискретной САУ с рассматриваемым регулятором можно записать n дискретных уравнений переходных состояний

(11.16)

где V[(k-1)T] – вектор состояния САУ на предыдущем такте управления;

– вектор состояния на текущем такте управления после замыкания ключевых элементов (фиксации новых значений измеренной координаты и ошибки регулирования);

Ф(К_j, Т) – расширенная матрица перехода системы, зависящая от искомых коэффициентов К_j ;

B(T) – матрица переключения импульсных элементов.

В результате решения системы n неоднородных алгебраических уравнений, составленных из дискретных уравнений состояний, находят численные значения коэффициентов К_j .

На заключительном этапе синтеза оптимальный регулятор представляют в виде дискретной передаточной функции

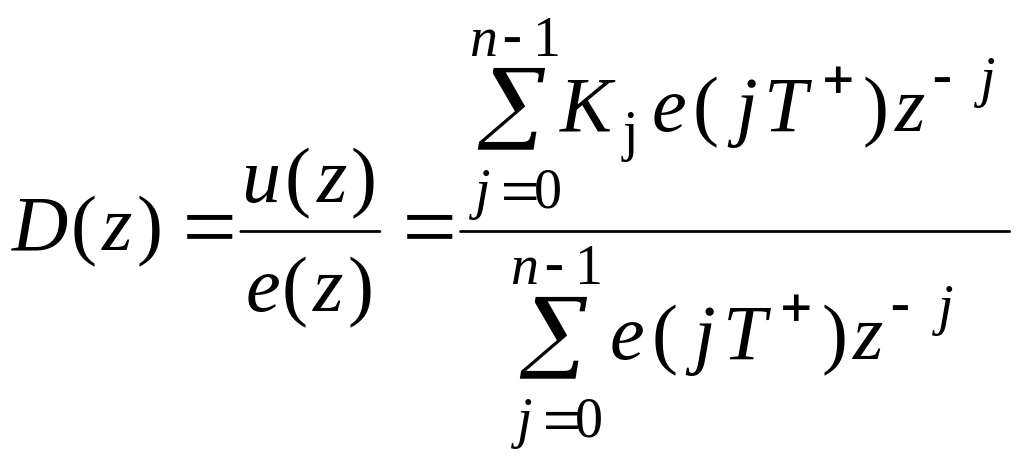. (11.17)

В отличие от рассмотренного ранее метода синтеза такт управления

здесь выбирается исходя из ограничений ресурсов управления (чем меньше требуемое время регулирования, тем большими ресурсами управления должна обладать САУ). В частности для цифровых электромеханических САУ в зависимости от регулируемой координаты значение Т находится в пределах 0,005…0,05 с.

К существенным недостаткам метода следует отнести довольно высокую чувствительность синтезированных САУ к вариациям параметров объекта управления и “чужим” аддитивным воздействиям. Например, система, оптимизированная по критерию быстродействия по задающим воздействиям, может оказаться далеко не оптимальной в смысле этого критерия при отработке возмущающих воздействий.

11.3.3 Метод синтеза апериодических дискретно-непрерывных

САУ с регуляторами состояния

Многие системы управления относятся к классу систем, функционирующих в режимах малых отклонений координат: систем стабилизации той или иной технологической координаты (скорости вращения или перемещения рабочего органа, температуры, давления, натяжения и т. п.), следящих систем управления, систем воспроизведения движений. Поскольку основным технологическим требованием при синтезе таких систем является максимальное быстродействие и минимум динамической ошибки отработки рассогласований заданных и действительных значений координат состояния, в качестве дискретного критерия оптимальности примем критерий вида , где – число периодов дискретного управления, по истечении которых система приходит в установившееся состояние без перерегулирования выходной переменной.

Синтез апериодических динамических систем, а именно такими являются системы, гарантирующие отсутствие перерегулирования в замкнутых дискретных САУ, традиционно проводят на основе идеальной компенсации нулей и полюсов объекта управления полюсами и нулями дискретной передаточной функции регулятора и добавления новых полюсов и нулей в соответствующих областях z - плоскости [1, 2]. Неточность математического описания, временной и температурный дрейф параметров объекта управления, ограничения в реализации передаточной функции регулятора техническими средствами приводят к неустойчивости замкнутой системы. Более того, такая процедура синтеза САУ даже при идеальной компенсации полюсов и нулей предполагает “апериодичность” переходных процессов только по отношению к входным воздействиям определенного вида и места их приложения. По отношению к “чужим” входным воздействиям система может иметь неприемлемое качество. В этой связи синтез САУ предлагается осуществлять на основе контроля полного состояния системы и реализации апериодических регуляторов состояния.

Ниже рассмотрена аналитическая процедура синтеза апериодических регуляторов состояния, обеспечивающих апериодические переходные процессы в линейных системах произвольного порядка. Предлагаемая процедура синтеза обеспечивает в системе управления астатизм первого порядка по задающим воздействиям, а, следовательно, повышенную точность отработки изменяющихся во времени задающих воздействий САУ.

Пусть линейный стационарный объект управления описывается дискретно-непрерывным векторно-матричным уравнением

, (11.18)

где – векторы состояния, управления и возмущения соответственно размерности ;

– матрицы состояния, управления, возмущения размерности соответственно;

T – такт дискретного управления;

k – номер такта дискретного управления.

Задача синтеза формулируется следующим образом: необходимо для произвольных начальных значений и постоянного на интервале nT вектора возмущений F(t) сформировать дискретную управляющую последовательность (U kT), k=0, 1, ... , переводящую объект управления (11.18) в заданное конечное состояние за n тактов управления, где n – порядок динамического объекта. Допущения при синтезе оптимального управления: время измерения координат состояния и выработки (вычисления) координаты управления ничтожно мало в сравнении с тактом T управления; длина разрядной сетки ЭВМ и устройств связи с объектом управления позволяет пренебречь квантованием непрерывных сигналов по уровню; значение периода управления T предполагается априори выбранным исходя из ограничений ресурсов управления. Приведенные допущения являются широко распространенными при синтезе дискретных систем управления объектами рассматриваемого класса [3].

Представим искомую управляющую дискретную последовательность в виде линейной формы дискретных значений векторов состояния X(kT), задающих воздействий X^*(kT), вектора возмущения F(kT) и вектора производных задающих воздействий в виде

. (11.19)

В этом уравнении – матрицы соответственно размерности , определение которых и является задачей синтеза.

Предлагаемый подход основан на разных формах представления объекта управления (в виде непрерывной модели) и устройства управления (в виде дискретной модели), причем структура устройства управления предполагается заданной не в виде дискретной передаточной функции, а в виде линейного дискретного регулятора состояния системы.

Векторная структурная схема такой дискретно-непрерывной системы приведена на рис. 11.6.

Рис. 11.6 Векторная структурная схема дискретно-непрерывной САУ

Пунктирными линиями на схеме выделены объект управления (ОУ) и устройство управления (УУ) - дискретный регулятор состояния. Дискретизация вектора управления и, соответственно, всех аддитивных воздействий осуществляется в моменты времени kT (k = 0, 1, 2, …) методом интерполяции нулевого порядка. Экстраполятор (фиксатор) нулевого порядка обозначен на схеме аббревиатурой ЭНП. Простейшая аппаратная реализация векторного ЭНП - m устройств выборки-хранения, имеющих общий квантователь сигналов в моменты времени kT (m – размерность вектора управления). При микропроцессорной реализации дискретного регулятора состояния ЭНП – совокупность регистров памяти с перезаписью информации с тактом T управления.

Заметим, что линейность моделей (11.18) объекта управления и регулятора (11.19) состояния объекта управления позволяет при синтезе САУ применить принцип суперпозиции управляемых динамических процессов. Проведем декомпозицию управляющей дискретной последовательности и динамических процессов в системе на две составляющие – управляемый свободный процесс и управляемый вынужденный процесс. В соответствие с этим в процедуре синтеза выделим два этапа – синтез свободного и синтез вынужденного движений.