7.3.3 Структурно устойчивые и структурно неустойчивые системы. Понятие d-разбиения

Структурно устойчивой системой называется система, устойчивости которой можно добиться, изменяя параметры звеньев. При этом тип звеньев и их соединения, т. е. структура САУ, остаются неизменными.

Структурно неустойчивой системой называется система, устойчивость которой может быть достигнута только при изменении структуры (заменой типов звеньев и характеров соединений).

Теория устойчивости позволяет не только определить устойчивость системы, но и влияние некоторых параметров системы на ее устойчивость и качество. Данное влияние определяется с помощью процедуры D-разбиения. Рассмотрим влияние какого-либо одного параметра на устойчивость системы (D-разбиение по одному параметру).

Пусть характеристическое уравнение системы имеет вид (7.9). Допустим также, что в системе есть некоторый, в общем случае комплексный, параметр k, который можно изменять и который входит линейно в характеристическое уравнение.

Тогда характеристическое уравнение (7.9) можно разбить на 2 части:

.

Отобразим в плоскость k мнимую ось плоскости корней p_i, определяющую границу области устойчивости системы, заменив p на . Тогда

(7.25)

где М(р) – члены характеристического уравнения, не содержащие параметр k, а D(p) – члены характеристического уравнения, содержащие параметр k линейно.

Непрерывно увеличивая от -¥ до +¥ построим в плоскости комплексного переменного k кривую D-разбиения. При этом левую часть кривой, обозначающую границу области устойчивости системы, будем штриховать. Только замкнутая область D определяет пределы изменения данного параметра, при которых система является устойчивой. На рис. 7.8 приведен пример построения кривой D-разбиения. Если подобных областей разбиения не оказывается, то система считается структурно неустойчивой и ввести ее в установившееся состояние возможно, лишь изменив структуру.

Если изменяемый параметр k является вещественным, то область его значений, при которых САУ остается устойчивой, принадлежит отрезку

(a, b), т. е. .

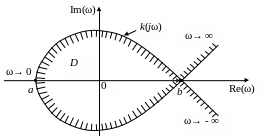
Рис. 7.8 Построение области D-разбиения

7.3.4 Логарифмический критерий устойчивости

Логарифмический критерий устойчивости применяется как для оценки устойчивости системы, так и при проектировании корректирующих звеньев, выводящих исходную систему из неустойчивого в устойчивое состояние. В основе логарифмического критерия устойчивости лежит критерий устойчивости Найквиста.

По критерию Найквиста базовая точка (-1; j0) в комплексной плоскости, определяющая границу устойчивости, характеризуется параметрами

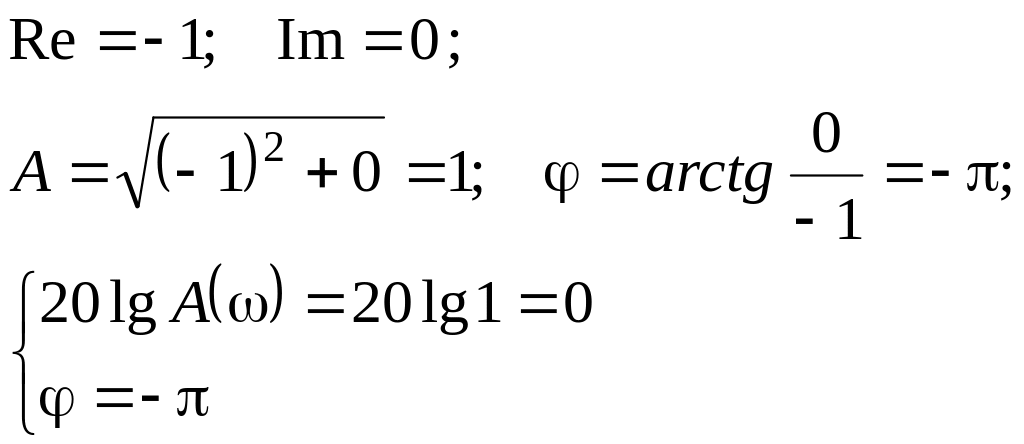
Рассмотрим частотные характеристики разомкнутой системы (диаграммы Боде) для двух случаев.

1. Система в разомкнутом состоянии устойчива.

Это означает, что годограф Найквиста (рис 7.9а) такой системы не пересекает отрезок . САУ в замкнутом состоянии будет устойчива, если частота среза ω_c логарифмической амплитудно-частотной характеристики (ЛАЧХ) разомкнутой системы меньше частоты, при которой логарифмическая фазовая частотная характеристика (ЛФЧХ) достигает значения -p, т.е. при положительных значениях ЛАЧХ до частоты среза ЛФЧХ не должна достигать угла -p. Диаграмма Боде устойчивой системы приведена на рис. 7.9б.

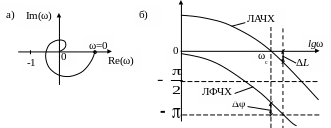
Рис. 7.9 Годограф Найквиста и логарифмические частотные характеристики

устойчивой системы при отсутствии правых корней разомкнутой САУ

2. Разомкнутая система неустойчива.

Логарифмический критерий устойчивости заключается в следующем: для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы при положительных значениях ЛАЧХ до частоты среза, количество переходов прямой -p ЛФЧХ было равно нулю (т.е. количество положительных переходов должно быть равно количеству отрицательных переходов). Годограф Найквиста и диаграмма Боде устойчивой системы приведены на рис. 7.10.

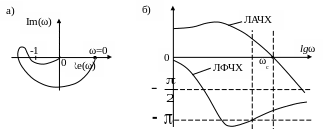
Рис. 7.10 Годограф Найквиста и логарифмические частотные характеристики

устойчивой системы при наличии правых корней разомкнутой САУ