7.3.2 Критерий Найквиста

В отличие от критериев Гурвица, Рауса и Михайлова, которые основаны на анализе характеристического уравнения замкнутой системы, критерий Г. Найквиста позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой характеристике разомкнутого контура системы. В этом заключается существенное преимущество критерия, т.к. построение АФЧХ разомкнутого контура для большинства реальных систем оказывается проще, чем построение годографа Михайлова. Особенно упрощается это построение для одноконтурных систем, состоящих из типовых звеньев.

Найквист в своем критерии рассматривает вспомогательную функцию, определяемую по формуле

, (7.21)

где - частотная передаточная функция разомкнутого контура.

Для физически реализуемых САУ степень полинома не выше степень полинома . Тогда степени числителя и знаменателя в (7.21) одинаковы и равны n.

Полюса этой передаточной функции являются полюсами разомкнутой САУ, а нули - полюсами замкнутой системы. Для устойчивости замкнутой системы необходимо и достаточно, чтобы все нули (7.21) располагались в левой половине комплексной плоскости.

Согласно теореме Коши [5] необходимо на комплексной плоскости выбрать контур (контур Найквиста), который охватывал бы всю ее правую половину, и исследовать, не находятся ли внутри ее какие-либо нули функции (7.21). Конформное отображение контура Найквиста в плоскость сводится к построению на комплексной плоскости вектора (годографа Найквиста), начало которого находится в точке (-1, j0), а конец скользит при изменении частоты от 0 до ∞ по АФЧХ разомкнутой системы .

Аргумент частотной передаточной функции (7.21) при изменении частоты от 0 до ∞ определяется формулой

. (7.22)

Рассмотрим три случая.

1. Система в разомкнутом состоянии устойчива.

Тогда для устойчивости замкнутой системы в соответствие с (7.22) необходимо, чтобы

.

Система в замкнутом состоянии будет устойчива, если изменение аргумента функции j(jw) при изменении частоты от 0 до ¥ составит ноль.

Критерий Найквиста для первого случая:

замкнутая система будет устойчивой, если АФЧХ разомкнутой системы не пересекает отрезок (-¥; -1), т.е. не охватывает критическую точку (-1; j0).

На рисунке 7.5а изображен годограф системы, устойчивой в замкнутом состоянии, а на 7.5б – неустойчивой системы.

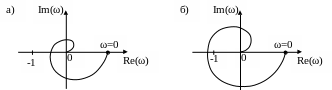
Рис. 7.5 Годографы Найквиста устойчивой (а) и неустойчивой (б) системы

Система находится на границе устойчивости, если годограф, соответствующий амплитудно-фазовой характеристики разомкнутой системы, хотя бы один раз пересечет точку (-1; j0).

2. Разомкнутая система неустойчива, причем число ее правых корней равно m.

Замкнутая система устойчива, если изменение аргумента при изменение частоты от 0 до ¥ представляется формулой:

.

При анализе устойчивости системы будем считать положительным переходом годографа при изменении частоты от 0 до ¥ пересечение им отрезка вещественной оси (-¥, -1) сверху вниз, отрицательным - снизу вверх. Если АФЧХ начинается на отрезке (-¥, -1), то будем считать это за 0,5 перехода с соответствующим знаком. Тогда критерий Найквиста звучит так:

если система неустойчива в разомкнутом состоянии и имеет m положительных корней, то система в замкнутом состоянии будет устойчива лишь в том случае, если разность между количеством положительных переходов и количеством отрицательных переходов отрезка действительной оси будет равна m/2, т.е. если годограф разомкнутой системы пересекает отрезок в положительном направлении m/2 раз.

3. Система в разомкнутом состоянии устойчива, однако введение обратной связи делает ее неустойчивой.

Замкнутая система неустойчива, если изменение аргумента при изменении частоты от 0 до ¥ представляется формулой:

.

Критерий Найквиста для данного случая звучит так:

если система в разомкнутом состоянии устойчива, а в замкнутом состоянии неустойчива, то годограф пересекает отрезок в отрицательном направлении m/2 раз.

Объединяя все три случая можно дать следующее определение критерия Найквиста:

система в замкнутом состоянии будет устойчива, если разность между числами положительных и отрицательных переходов годографа разомкнутой системы отрезка действительной оси будет равна m/2, где т – количество корней характеристического уравнения разомкнутой системы, находящихся в правой полуплоскости.

Диаграмму Найквиста можно построить вручную для нескольких значений частоты ¥. Вместе с тем, построение диаграммы Найквиста существенно упрощается при использовании функции nyquist системы программирования Matlab.

Рассмотрим пример. Пусть передаточная функция устойчивой разомкнутой САУ имеет вид:

. (7.23)

Запишем скрипт Matlab:

>> num=[0.4]; den=[1 2 1 0.6]; den1=[1 2 1 1];

>> sys=tf(num,den);

ans =

>> roots(den)

-1.6104

-0.1948 + 0.5785i

-0.1948 - 0.5785i

>> roots(den1)

ans =

-1.7549

-0.1226 + 0.7449i

-0.1226 - 0.7449i

>> nyquist(sys).

Команда roots(den) возвращает значения корней разомкнутой САУ, а команда roots(den1) определяет корни замкнутой САУ. Как видим, все три корня замкнутой САУ имеют отрицательные вещественные части, а, значит, система устойчива.

На рис. 7.6 приведена диаграмма Найквиста, которая, как видим, не охватывает точку (-1, j0) комплексной плоскости. Это позволяет говорить об устойчивости замкнутой САУ без нахождения корней характеристического уравнения.

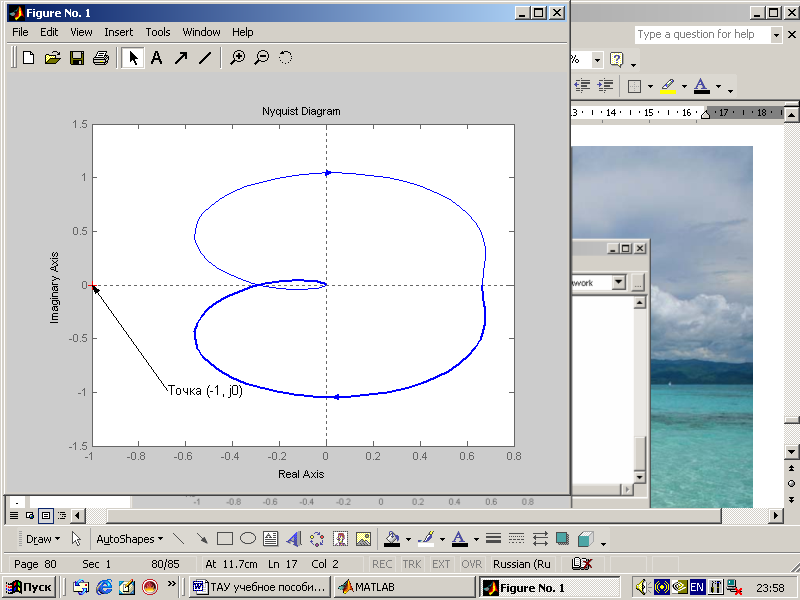
Рис. 7.6 Пример применения функции nyquist системы MATLAB

для первого случая

Поскольку функция nyquist применена без указания параметров, то диаграмма строится автоматически для всего диапазона изменения частоты и полный годограф Найквиста симметричен относительно действительной оси.

Рассмотрим еще один пример. Пусть разомкнутая САУ 4-го порядка (n=4) устойчива и имеет передаточную функцию

. (7.24)

Определим устойчивость замкнутой САУ по критерию Найквиста. Запишем скрипт Matlab:

>> num=[4];

>> den=[1 2 3 4 1];

>> den1=[1 2 3 4 5];

>> sys=tf(num,den);

>> roots(den)

ans =

-0.1018 + 1.4711i

-0.1018 - 1.4711i

-1.4873

-0.3092

>> roots(den1)

ans =

0.2878 + 1.4161i

0.2878 - 1.4161i

-1.2878 + 0.8579i

-1.2878 - 0.8579i

>> nyquist(sys).

Все корни разомкнутой системы являются левыми, т. е. m=0, а в замкнутой САУ имеется два правых корня, что свидетельствует об ее неустойчивости.

Аналогичный вывод можно сделать, рассматривая диаграмму Найквиста (рис. 7.7). Годограф Найквиста охватывает точку (-1, j0). Согласно критерию Найквиста система в замкнутом состоянии будет неустойчива, поскольку разность между числами положительных и отрицательных переходов годографа разомкнутой системы отрезка действительной оси равна единице (имеется один отрицательный переход действительной оси) при m/2=0.

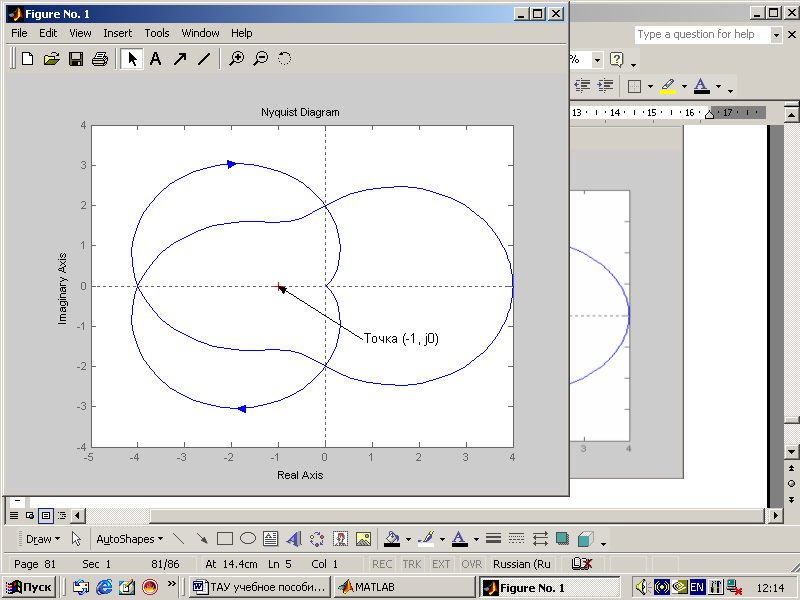
Рис. 7.7 Пример применения функции nyquist системы MATLAB

для третьего случая