Міністерство освіти і науки України

Рівненський державний гуманітарний університет

Затверджую

Проректор з навчальної роботи

____________(проф.Воробйов А.М.)

«____» «____________» 2009р.

Методика навчання математики в старшій школі. Частина 2. Практичні заняття

Методичні рекомендації вивчення курсу

для студентів спеціальності

Математика 7010103 освітньо – кваліфікаційний рівень спеціаліст

Рівне – 2009

УДК

ББК 22.1 р

С

Методика навчання математики в старшій школі. Практичні заняття. Методичні рекомендації вивчення курсу для студентів спеціальності Математика 7010103 освітньо-кваліфікаційний рівень спеціаліст. Частина 2. Рівненський державний гуманітарний університет. – 2009 р. - с.

Укладачі : кандидат педагогічних наук, доцент Белешко Д.Т.

кандидат педагогічних наук, доцент Кирилецька Г.М.

старший викладач, Клекоць Г.Я.

Рекомендовано до друку кафедрою математики та методики її викладання РДГУ (протокол № від р. )

Затверджено Вченою радою Рівненського державного гуманітарного університету.

Протокол № від «___» «__________» 2009 р.

ББК 22.1 р. С

РДГУ. 2009.

Зміст

1. Рівняння і нерівності у старшій школі………………………………..

2. Формування поняття функції…………………………………….

3. Границя функції. Неперервні і розривні функції………………

4. Початки диференціального числення в курсі алгебри і початків аналізу………

5. Вивчення інтеграла в курсі алгебри і початків аналізу……………………

6-7.Ймовірнісно – статистична змістовна лінія в шкільному курсі математики…….

8. Контрольна робота № 1…………………………………………………………….

9. Перелік……………………………………………………………………………..

Заняття №1

РІВНЯННЯ І НЕРІВНОСТІ У СТАРШІЙ ШКОЛІ

МЕТА:Ознайомитися з видами рівнянь і нерівностей, які вивчаються в курсі алгебри і початків аналізу, та з деякими питаннями методики їх розв'язування.

ПЛАН

1. Особливості розв'язування алгебраїчних рівнянь, нерівностей та їх систем у 10 і 11 класах профільної школи.

2. Розв'язування ірраціональних рівнянь та нерівностей.

3. Розв'язування показникових і логарифмічних рівнянь,нерівностей.

4. Методика розв'язування тригонометричних рівнянь і нерівностей у 10 класі.

4. Розв'язування рівнянь і нерівностей з модулями.

ЛІТЕРАТУРА

1. Бевз Г.П. Методика викладання математики: Навч. посібник. – 3-те вид., перероб. і доп. – К.: - Вища шк., 1989. – 367 с.

2. Блох А.Ш., Трухан Т.Л. Неравенства. – Минск: Народная асвета, 1972.

3. Дорофеев Г.В. О корнях показательно-степенных уравнений. Математика в школе, 1972, № 2.

4. Жовнір Я.М., Рябчинська В.Д. Показникові і логарифмічні нерівності та рівняння. У зб.: У світі математики, вип. 7. – К.: Радянська школа, 1976.

5. Колягин Ю.М. и др. Методика преподавания математики в средней школе. – М.: Просвещение, 1977.

6. Пойа Д. Как решать задачу: Пер. с англ. – М.: Учпедгиз, 1959. – 207 с.

7. Програми для загальноосвітніх навчальних закладів.

Математика. 5—11-і класи│В. Г. Бевз, А.Г. Мерзляк, 3.1. Слєпкань

││Математика.Програма для загальноосвітніх навчальних закладів.

─К.:2003р.Навчальна книга С. 4 – 52.

8. Програми для загальноосвітніх навчальних закладів, спеціалізованих шкіл, гімназій, ліцеїв економічного профілю. Математика. 10—11-і класи │ М.А. Ваинтрауб, О.С. Стрельченко, І.Г. Стрельченко ││Математика.Програма для загальноосвітніх навчальних закладів. ─К.:2003р. Навчальна книга С. 53 – 69.

9. Програми для загальноосвітніх навчальних закладів, спеціалізованих шкіл, гімназій, ліцеїв природничного профілю. Математика. 10— 11-і класи │Я. С. Бродсъкий, О.Л. Павлов, А.К. Сліпенко, О.М. Афанасьева││Математика.Програма для загальноосвітніх навчальних закладів. ─К.:2003р.Навчальна книга С. 70 – 102.

10. Програми для загальноосвітніх навчальних закладів, спеціалізованих шкіл, гімназій, ліцеїв. Математика 8—11-і класи │ МІ. Бурда, М.А. Жалдак, Т. Колесник, Т.М. Хмара, М. Ядренко││ Математика. Програма для загальноосвітніх навчальних закладів. ─К.:2003р. Навчальна книга С. 103 – 130.

11. Програми для загальноосвітніх навчальних закладів, спеціалізованих шкіл, гімназій, ліцеїв фізико-математичного профілю. Математика. 10—11-і класи │ M.I. Бурда, М.А. Жалдак, Т. Колесник, Т.М. Хмара, М. Ядренко ││ Математика. Програма для загальноосвітніх навчальних закладів. ─К.:2003р. Навчальна книга С. 131 – 148.

12. Програми для загальноосвітніх навчальних закладів, спеціалізованих шкіл, гімназій, ліцеїв суспільно-гуманітарного, філологічного, художньо-естетичного та спортивного профілів. Математика. 10—11-і класи │ M.I. Бурда, Ю.І. Мальований││Математика. Програма для загальноосвітніх навчальних закладів. ─К.:2003р.

Програми факультативів, спецкурсів, гуртків

13. Факультативний курс загальноосвітніх навчальних закладів.

Математика. 7—9-і класи │ М.І. Бурда, В.Г. Бевз,

Н.С. Прокопенко││Математика. Програма для загальноосвітніх навчальних закладів. ─К.:2003р. Навчальна книга С. 149 – 159.

14. Савич Є.Ф. Використання похідної при розв'язуванні деяких трансцендентних нерівностей. – У зб.. Методика викладання математики, вип. 4. – К.: Радянська школа, 1968.

15. Савич Є.Ф. Деякі питання еквівалентності при розв’язуванні нерівностей. – У зб.: Методика викладання математики, вип. 10. – К.: Радянська школа, 1975.

16. Столяр А.А. Педагогика математики. – Минськ.: Вышейшая школа, 1977.

17. СлєпканьЗ.І. Методика навчання математики: Підруч.для студ. мат. Спеціальностей пед. навч. Закладів.-К.: Зодіак-ЕКО, 2000.-512с.

18. Слепкань З.И. Методика преподавания алгебры и начал анализа. – К. : Рад. шк., 1978. – 224 с.

19. Шкіль М.І. та інші. Алгебра і початки аналізу: підр. для 10 кл. загальноосвітніх навч. закладів / М.І.Шкіль, З.І.Слєпкань, О.С.Дубинчук. – К.: – Зодіак-ЕКО, 2006. – 272 с.

20. Шкіль М.І. та інші. Алгебра і початки аналізу: підр. для 11 кл. загальноосвітніх навч. закладів / М.І.Шкіль, З.І.Слєпкань, О.С.Дубинчук. – К.: – Зодіак-ЕКО, 2006. – 384 с.

МЕТОДИЧНІ ЗАУВАЖЕННЯ

Вивчення рівнянь і нерівностей продовжують у старших класах. У 10 класі при викладі теоретичного матеріалу вводять нові види рівнянь, нерівностей та їх систем, розглядають способи їх розв'язування. Рівняння і нерівності розв'язуються в 10 класі майже в кожній темі з курсу алгебри і початків аналізу. Відомі вже учням алгебраїчні рівняння і нерівності розв'язуються під час вивчення похідної та її застосування до дослідження функцій і розв'язування задач, учні знову розв'язують квадратичні нерівності, проте по-новому, на основі дослідження квадратичної функції за допомогою похідної.

ВИКОРИСТАННЯ ВЛАСТИВОСТЕЙ ФУНКЦІЙ ДЛЯ РОЗВ'ЯЗУВАННЯ РІВНЯНЬ
1.Скінченна ОДЗ
Якщо область допустимих значень (ОДЗ) рівняння (нерівності або системи) складається з скінченного числа значень, то для розв’язування досить перевірити всі ці значення.	Приклад. Розв'язання. ОДЗ: Перевірка: х=1 – корінь х=-1- не корінь Відповідь: х = 1
2. Оцінка лівої та правої частин рівняння
	Приклад. Розв'язання.
	Приклад. Розв'язання. Оскільки , , то задане рівняння рівносильне системі З першого рівняння одержуємо х=2, що задовольняє всю систему. Відповідь: х=2.
3. Використання монотонності
Схема розв'язування
1. Підбираємо один або декілька коренів рівняння 2. Доводимо, що інших коренів це рівняння не має (використовуючи теореми про корені рівнянь або оцінку лівої та правої частин)
Теореми про корені рівнянь
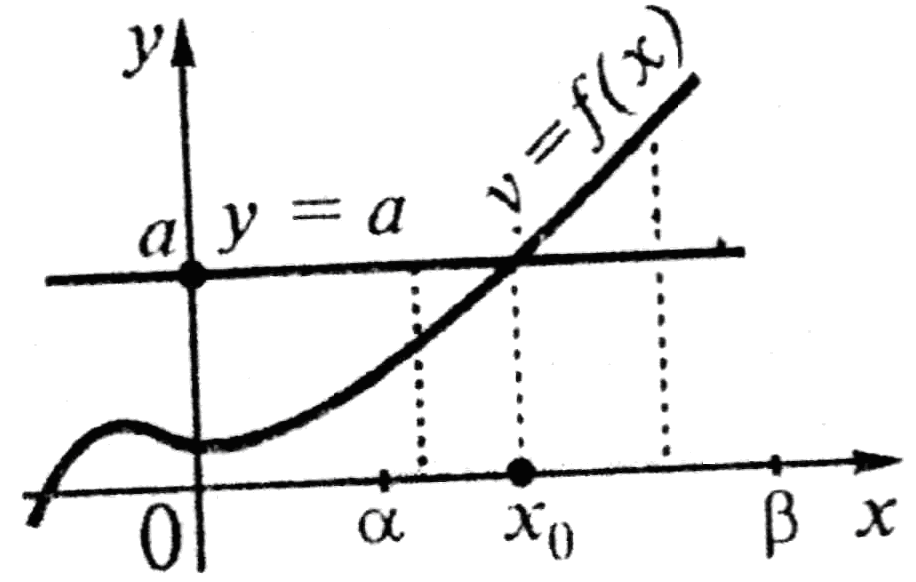
Теорема 1. Якщо в рівнянні f(х) = а функція f(х) зростає (спадає) на деякому проміжку, то це рівняння може мати не більше ніж один корінь на цьому проміжку.	Приклад. Рівняння має єдиний корінь х=1 ( , тобто 2=2), оскільки функція зростає (на всій О.В. х≥0).

Теорема 2. Якщо в рівнянні f(x) = g (х) функція f(х) зростає на деякому проміжку, а функція g(х) спадає на цьому самому проміжку (або навпаки), то це рівняння може мати не більше ніж один корінь на цьому проміжку	Приклад. Рівняння має єдиний корінь х = 2 (22 =6-2, тобто 4 = 4), оскільки f(x)=2x зростає, а g(x)=6 спадає.
4. «Шукай квадратний тричлен»
І Спробуйте розглянути задане рівняння як квадратне відносно якоїсь змінної (чи відносно якоїсь функції)	Приклад. 4х - (7 - х) 2х + 12 - 4х = 0 Розв'язання. Запишемо, що 4х = 22x і введемо заміну 2x = t. Одержуємо t2 – (7-x)t+12-4x. Розглянемо це рівняння як квадратне відносно t. Його дискримінант D = (7 - х)2 - 4(12 - 4х) = х2 + 2х + 1 = (х + 1)2. Тоді , тобто t1=4, t2=3-x. Обернена заміна дає: 2х = 4 (звідси х = 2) або 2х = 3 - х (має єдиний корінь х = 1, оскільки f(х) = 2х – зростає, а g(х) = 3 - х – спадає) Відповідь: 1; 2.

У 10 класі розглядаються найпростіші ірраціональні рівняння, розв'язання яких в основному зводиться до квадратних. Учні повинні засвоїти, що при піднесенні обох частин рівняння до парного степеня, можуть з'явитися сторонні корені, які відкидаються в результаті перевірки. З'ясування причин виникнення сторонніх коренів програмою не передбачено, їх можна розглянути на заняттях математичного гуртка або на факультативі.

Записуючи, розв'язання систем, не треба вимагати, щоб на кожному кроці на основі вивчених теорем проводилося обґрунтування перетворення, яке не порушує рівносильності системи, але важливо при цьому, щоб учні вміли застосовувати ці теореми і при нагоді змогли провести таке обґрунтування.

У 10 класі розглядаються також і деякі трансцендентні рівняння і нерівності: (показникові та логарифмічні).

Після вивчення основної логарифмічної тотожності ( )для рівнянь виду доцільно розглянути ще один спосіб розв'язування, а саме:

( ) ( ) (х = log_ab) ( ).

У 10 класі розглядаються також тригонометричні рівняння і нерівності. Перш ніж почати розв'язувати конкретні рівняння, треба, щоб учні навчилися свідомо знаходити значення обернених тригонометричних функцій, особливо тоді, коли значення аргу­менту є від'ємне число. Найбільші труднощі виникають при обчисленні arccos а і arcctg а для а<0. Для таких рівнянь, як sin х = 0, sin х = ±1; соs х = 0, соs х = ±1, tg х = 0, ctg х = 0, множину коренів учні повинні знаходити усно. Якщо значення синуса від'ємне, то слід привчити учнів у формулі відразу писати –1 в степені n + 1. Наприклад, для sin x = – матимемо х =(–1)ⁿ⁺¹ +πn, n Z (учні часто пишуть неправильно: х = (–1)ⁿ⁺¹ +πn).

Якщо перед змінною х стоїть знак «–», то доцільно замінити його на «+», використовуючи при цьому властивість парності чи непарності відповідної тригонометричної функції.

Із способом розкладання на множники учні знайомі ще у 7 і 8 класах. У 10 і 11 класах слід звернути увагу на одну дуже суттєву деталь: добуток дорівнює нулю не тільки тоді, коли принаймні один з множників дорівнює нулю, а й тоді, коли інші множники при цьому не втрачають зміст. Підтвердженням цієї думки є рівняння tg xcosх = 0, множина розв'язків якого знаходиться тільки при умові, що tg x = 0, оскільки для х, при яких cos x = 0, значення тангенса не існують.

Рівняння виду аsin х + bсоs х = с розв'язують заміною sin x і соs х на tg . Слід сказати, що цей спосіб розв'язання не є одним з кращих, бо він досить громіздкий і приводить, взагалі кажучи, до порушення рівносильності (втрати розв'язків). Рівняння, лінійні відносно sin х і cos х, краще розв'язувати за допомогою введення допоміжного кута (в посібнику для 10 класу цей спосіб не розглядається).

У 10 класі починають розв'язувати найпростіші тригонометричні нерівності. Крім запропонованого у підручнику способу , пропонуємо показати учням і графічний метод розв’язування. Алгоритм розв'язання пропонується такий (покажемо на прикладі sin x > a, |a| < 1):

1) будують графіки функцій у = sin х і у = а; 2) на рисунку позначають один з проміжків, наприклад на [ ], завдовжки 2π, де sin х > а, і записують його; 3) скориставшись властивістю періодичності функції у = sin х, дістають відповідь.

Застосування графічного методу полегшує знаходження кінцевих значень проміжку. Проте на побудову графіків функцій витрачається багато часу навіть тоді, коли є шаблони. Тому найдоцільніше використовувати одиничне коло, за допомогою якого теж можна знайти розв'язки. При цьому треба звернути серйозну увагу на те, що при написанні числового проміжку [а; b], зображеного на одиничному колі, число а повинно бути меншим за число b, і що числа, зображені точками на такому колі, зростають в напрямі, протилежному до руху стрілки годинника.

Схема розв’язування більш складних тригонометричних рівнянь

1. Спробуємо всі тригонометричні функції звести до одного аргументу.

2. Якщо вдалося звести до одного аргументу, то спробуємо всі тригонометричні вирази звести до однієї функції.

3. Якщо до одного аргументу вдалося звести, а до однієї функції – ні, то спробуємо звести рівняння до однорідного.

4. У решті випадків переносимо всі члени в один бік і спробуємо одержати добуток або використовуємо спеціальні прийоми розв’язування.

5. Якщо в процесі розв’язування необхідне вибирання коренів тригонометричного рівняння, то проводимо відбирання на одному періоді, спільному для всіх функцій, що входять до запису рівняння (якщо він існує), а потім відповідь періодично продовжуємо.

Схема розв’язування більш складних тригонометричних нерівностей