Вопрос 32

Энтальпия и энергия Гиббса, их физический смысл, связь между ними.

Сумма внутренней энергии и произведения объёма вещества на внешнее давление наз. энтальпией: Н = U + pV. Энтальпия, подобно объему, давлению, температуре и внутренней энергии, явл. характеристикой состояния системы. Абсолютные значения Н не известны, т.к точно не известна величина внутренней энергии U. Научное и прак. значение имеет изменение энтальпии в ходе процесса, т.е разность: .

Энергия Гиббса − это термодинамический потенциал следующего вида: , где U − внутренняя энергия, P − давление, V − объем, T − абсолютная температура, S − энтропия. Энергию Гиббса можно понимать как полную химическую энергию системы (кристалла, жидкости и т. д.)

При постоянных температуре и давлении: TΔS ≥ ΔU + РΔV + A_пол A_пол ≥ ΔU + РΔV – TΔS = U₂ + РV₂ − TS₂ −(U₁ − РV₁ − TS₁) (*). Отсюда: наз. энергией Гиббса. ΔG ≤ −А_пол . Из определении этой функции следует, что абсолютное её значение неизвестно, изменение этой функции при переходе от начального состояния к конечному не зависит от пути перехода.

Физический смысл энтальпии и энергии Гиббса: физический смысл энтальпии: ее изменение — это тепло, подведенное к системе в изобарическом процессе (при постоянном давлении).

Энергия Гиббса в равновесном процессе с точностью до знака равна полезной работе, которую может совершить система.

Вопрос 33

Энергия Гиббса как термодинамическая функция состояния. Определение и свойства. Вычисление стандартной энергии Гиббса процесса по справочным данным. Критерий самопроизвольного протекания реакций.

Энергия Гиббса − это термодинамический потенциал следующего вида: , где U − внутренняя энергия, P − давление, V − объем, T − абсолютная температура, S − энтропия. Энергию Гиббса можно понимать как полную химическую энергию системы (кристалла, жидкости и т. д.).

Свойства: однозначная, конечная, непрерывная функция. Из её определения. следует, что абсолютное её значение неизвестно, изменение этой функции при переходе от начального состояния к конечному не зависит от пути перехода.

−A_пол ≥ ΔG.

Значит ΔG для обратимого процесса равно полезной работе системы. Физический смысл энергии Гиббса вытекает из соотношения (*) – энергия Гиббса в равновесном процессе с точностью до знака равна полезной работе, которую может совершить система. В случае протекания неравновесных процессов энергия Гиббса будет (с обратным знаком) равна максимально возможной полезной работе, которую может совершить система.

Вычисление стандартной энергии Гиббса процесса по справочным данным: по следствию из закона Гесса энергия Гиббса химической реакции может быть найдена:

ΔG_{хим.реакции} = ∑n_iG_{i(продуктов)} − ∑n_jG_{j(исх. в-в)} .

Вопрос 34

Критерий самопроизвольного протекания реакций, энтальпийный и энтропийный факторы процесса. Какие реакции протекают самопроизвольно в водных растворах?

При постоянных температуре и давлении: ΔG ≤ −А_пол. . При отсутствии полезной работы получаем: ΔG ≤ 0. Из этого соотношение следует, что при протекании обратимых хим. реакций ΔG = 0, а при протекании реальных, самопроизвольных процессов она уменьшается. Иными словами, при Р = const, Т = const самопроизвольно протекают только процессы, сопровождающиеся уменьшением энергии Гиббса. Пределом протекания процесса будет состояние с минимальным значением G при данных условиях. После достижения минимума G перестает изменяться и ΔG = 0, система находится в состоянии равновесия.

ΔG = ΔН – ТΔS. самопроизвольное течение процесса (ΔG< 0) возможно при:

• ΔН<0 и ΔS>0 ;

• ΔН>0 и ΔS>0, если ТΔS > ΔН ;

• ΔН<0 и ΔS<0, если |ΔН| > |ТΔS|.

Чем отрицательней ΔG, тем проще, в более мягких условиях идет процесс.

Энтальпийный и энтропийный факторы процесса:

Если ΔН<0 отражает стремление к объединению частиц в более крупные агрегаты, то ΔS>0 отражает стремление к беспорядочному расположению частиц, к их дезагрегации. Переход системы в состояние с минимальной энергией когда ΔS=0, если же ΔН=0, то система самопроизвольно переходит в наиболее неупорядоченное состояние. Каждая их этих противоположных тенденций, количественно выражаемых ΔН и ΔS зависит от природы вещества и условий протекания процесса (т-ра, давление, соотношение между реагентами и т.д).

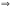
Произведение ТΔS (кДж/моль) явл. энтропийным фактором процесса, ΔН – энтальпийным фактором. В состоянии равновесия: ΔН = ТΔS. Это уравнение явл. условием равновесия, характеризует такое состояние данной системы, когда скорости протекающих в ней противоположных процессов становятся равными. Из этого уравнения : расчет изменения энтропии в равновесном процессе возможен из непосредственно измеряемых величин. ΔН фазового перехода можно определить экспериментально с помощью калориметра.