1.9. Контрольные задания

Дано комплексное число z. Требуется:

1. записать число z в алгебраической, тригонометрической и показательной формах;

2. возвести в степень z³;

3. найти корни уравнения 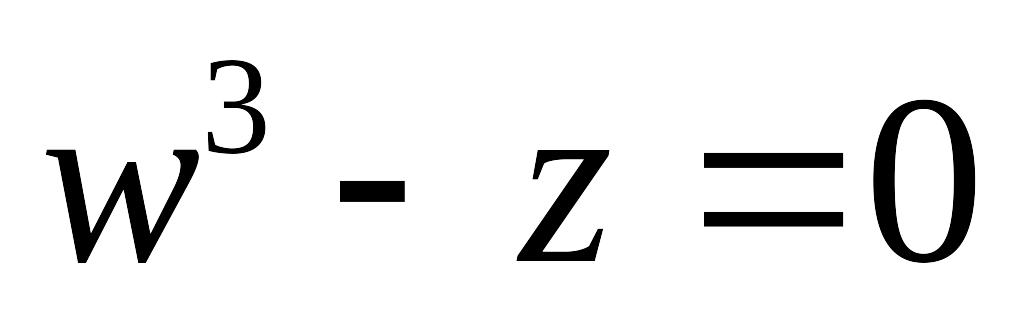при следующих значениях z:

1.10. Типовой расчет

Даны три комплексных числа: , , , (N = ).

1. Найти тригонометрическую и показательную формы этих чисел.

2. Вычислить 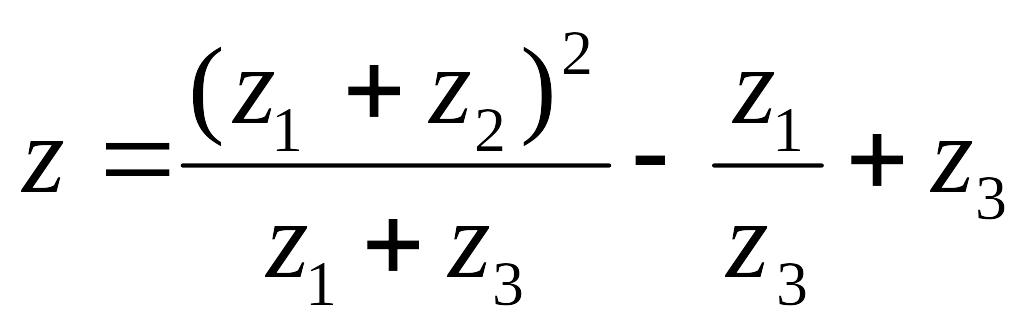и .

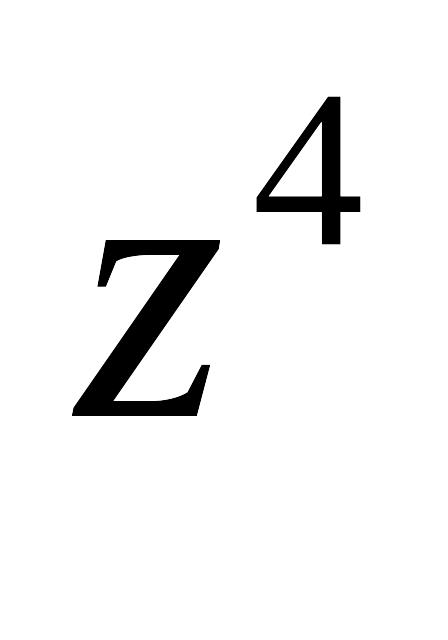3. Решить уравнение .

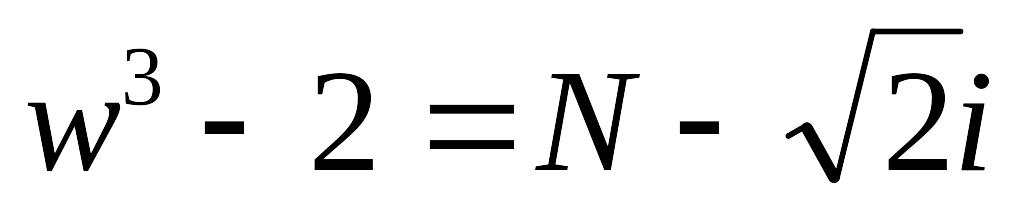1.11. Вопросы для самопроверки

1. Комплексные числа. Их изображение на плоскости.

2. Модуль и аргумент комплексного числа.

3. Различные формы представления комплексного числа.

4. Операции над комплексными числами в алгебраической форме.

5. Операции над комплексными числами в тригонометрической форме.

6. Формула Муавра. Вычисление корней n-ой степени из комплексного числа.

7. Операции над комплексными числами в показательной форме.

1.12. Вопросы для теоретического опроса

1. Комплексные числа. Их изображение на плоскости.

2. Модуль и аргумент комплексного числа. Различные формы представления комплексного числа.

3. Операции над комплексными числами. Формулы Эйлера и Муавра. Вычисление корней n-й степени из комплексного числа. Возведение комплексного числа в комплексную степень.

2. Многочлены

Определение. Многочленом (или полиномом) степени n одного неизвестного х называется выражение вида

.

Определение. Выражение вида называется членом многочлена f(x), числа ( или ( )) называются коэффициенты многочлена f(x). Число называется свободным членом многочлена.

Определение. Степенью многочлена называют наибольший номер отличного от нуля коэффициента многочлена f(x):

.

При этом называется старший членом многочлена, а – старшим коэффициентом многочлена.

2.1. Действия над многочленами

Пусть даны два многочлена f(x) и g(x):

и

Определение. Два многочлена n-ой степени f(x) и g(x) называются равными, если равны соответствующие коэффициенты этих многочленов, т.е.

.

1. Сложение многочленов.

Определение. Если даны два многочлена f(x) и g(x):

и , ,

то под суммой многочленов понимается многочлен

,

где

2. Умножение многочленов.

Определение. Если даны два многочлена f(x) и g(x):

и , ,

то под произведением многочленов понимается многочлен

, , где .

Таким образом, результат произведения многочленов – многочлен, составленный как сумма всевозможных попарных произведений членов первого многочлена на члены второго. В частности,

Теорема. Множество всех многочленов с действительными или комплексными коэффициентами, рассматриваемые вместе с определенными на нем операциями сложения и умножения, образуют кольцо, т.е.

1. ;

2. ;

3. ;

4. ;

5. 

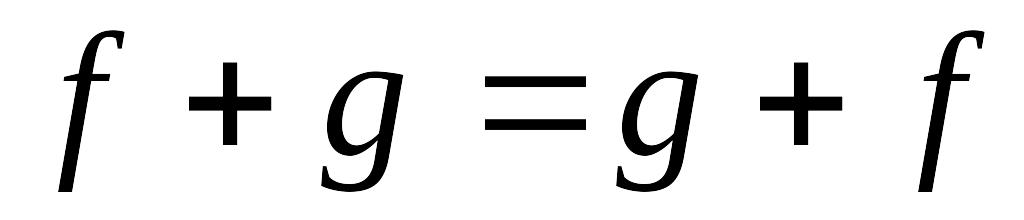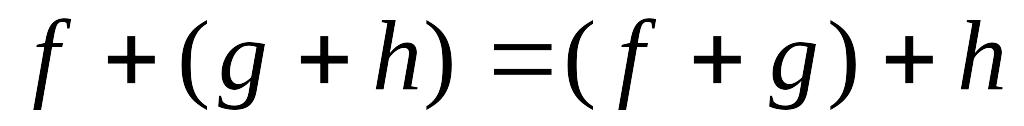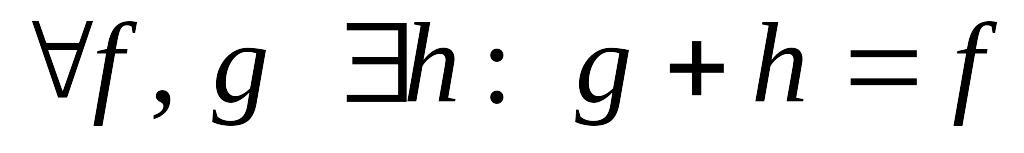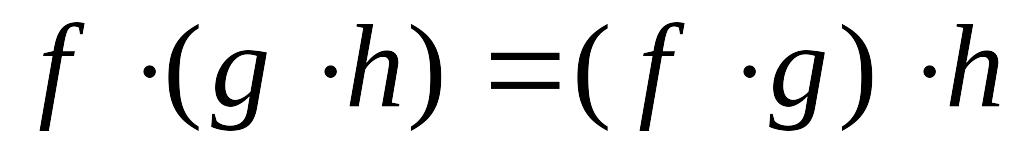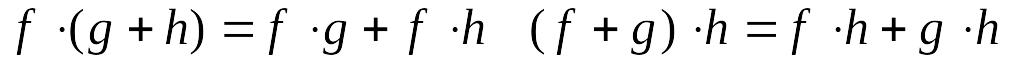
Лемма. Пусть f(x) и g(x) – ненулевые многочлены

,

, ,

Тогда степень суммы многочленов не превосходит максимума степеней слагаемых, а степень произведения равна сумме степеней сомножителей.

.