9.3. Зависимость между матрицами одного и того же преобразования в различных базисах. Подобные матрицы

Рассмотрим в конечномерном линейном пространстве Rⁿ два базиса и ; первый из них назовем старым, второй – новым.

Теорема. Если и – два базиса линейного пространства Rⁿ, А – матрица линейного преобразования в старом базисе, то матрица этого преобразования в новом базисе имеет вид:

,

где С – матрица перехода от старого базиса к новому.

Определение. Матрица называется подобной матрице А, если существует невырожденная квадратная матрица С, удовлетворяющая равенству

Следствие. Если линейное преобразование имеет невырожденную матрицу в некотором базисе, то матрица этого преобразования будет невырожденной в любом другом базисе.

Пример. В базисе преобразование имеет матрицу:

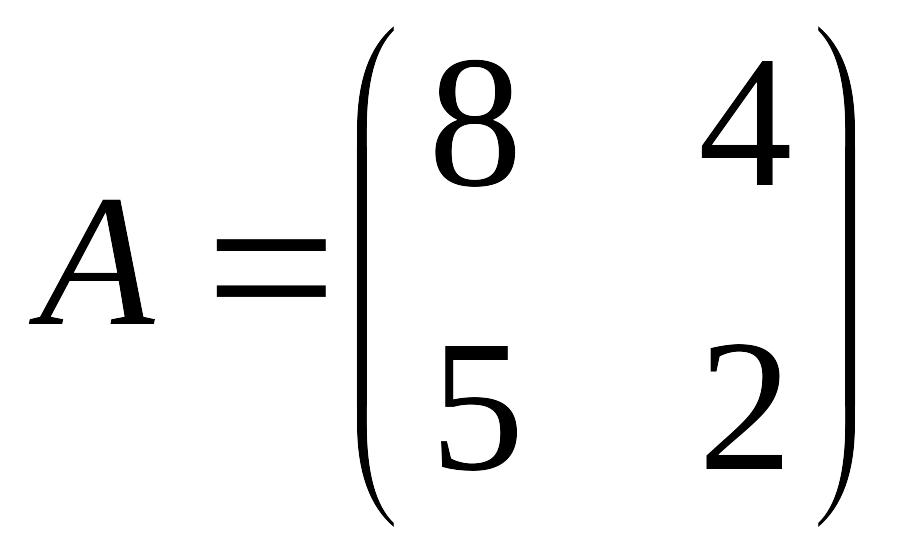
Найти матрицу оператора в базисе .

Решение.

Матрица перехода от старого базиса к новому С: .

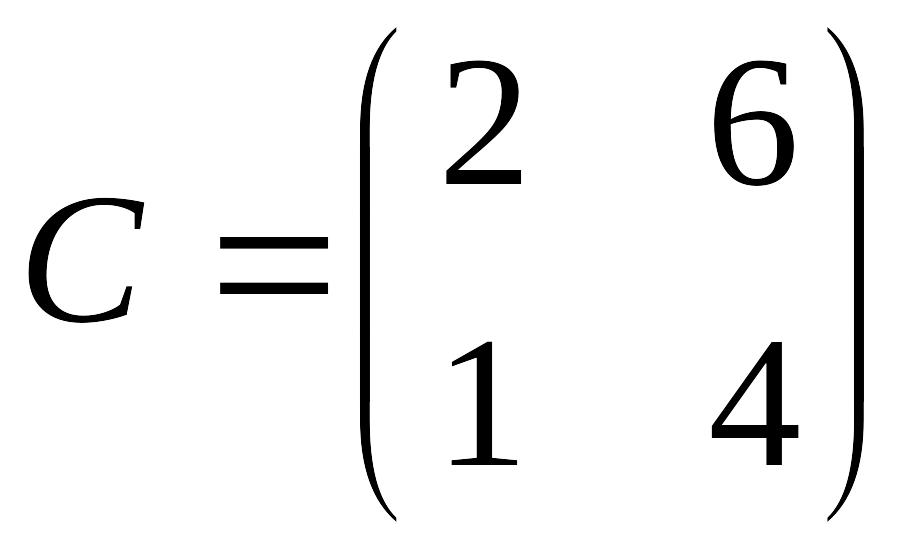Тогда обратная матрица С^–1: .

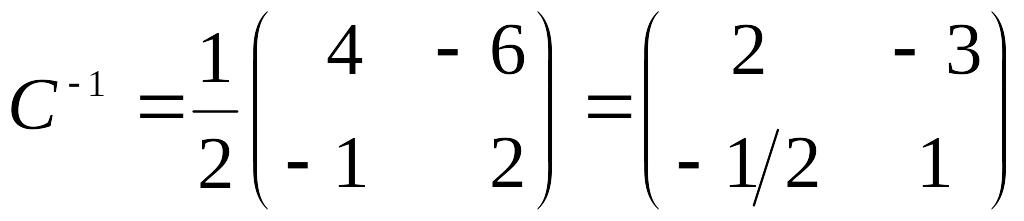По формуле получаем:

.

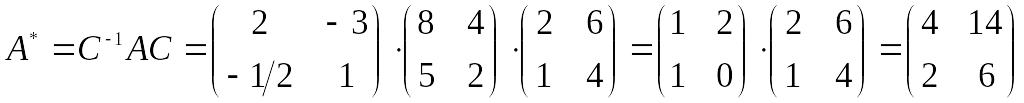9.4. Действия над линейными операторами

1. Сложение линейных операторов.

Определение. Суммой двух линейных операторов и некоторого пространства Rⁿ называется такой оператор , что для любого вектора этого пространства выполняется равенство: .

Если в некотором базисе линейные операторы и имеют соответствующие матрицы А и В, то их оператор в том же базисе имеет матрицу А+В.

Свойства операции сложения:

1. ;

2. ;

3. 

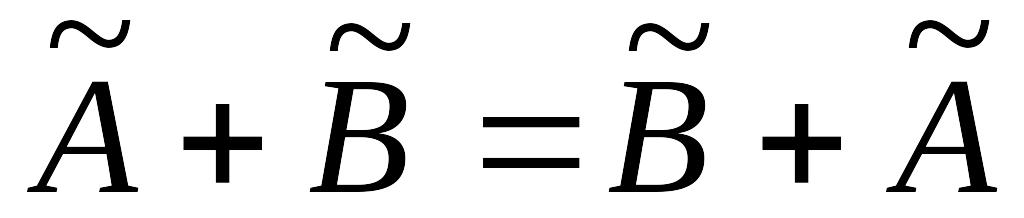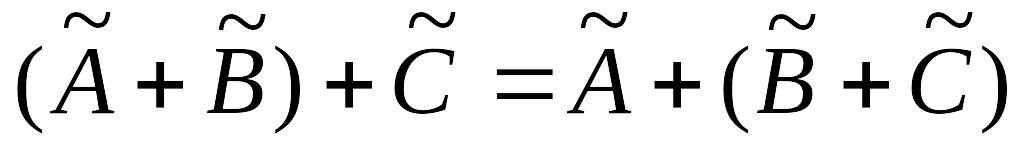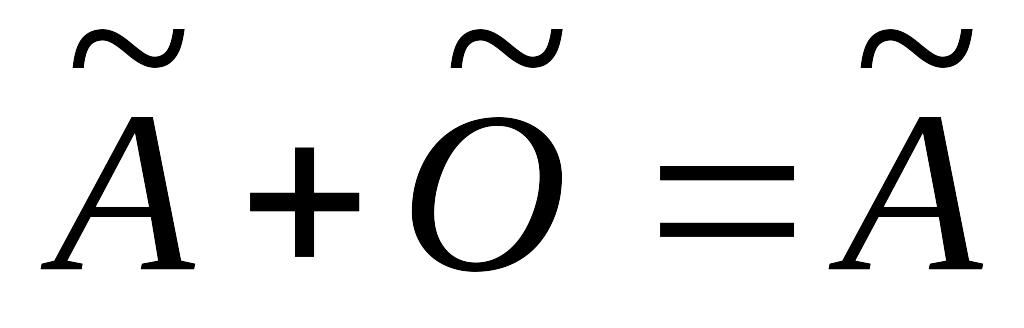
2. Умножение линейного оператора на число.

Определение. Произведением линейного оператора некоторого пространства Rⁿ на число λ называется оператор , определяемый равенством

для любого вектора этого пространства.

Свойства операции умножения линейного оператора на число:

1. ;

2. ;

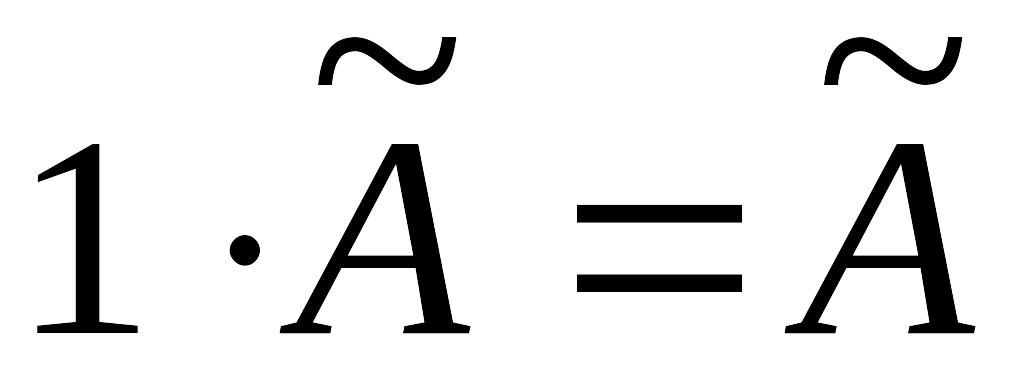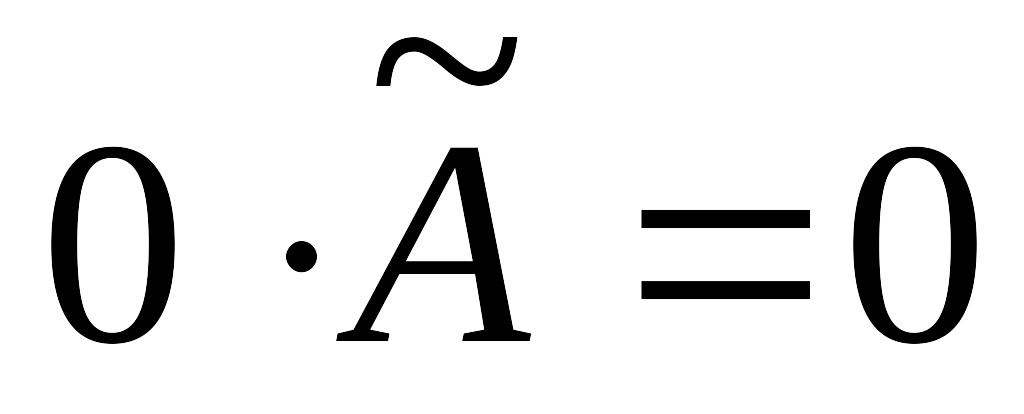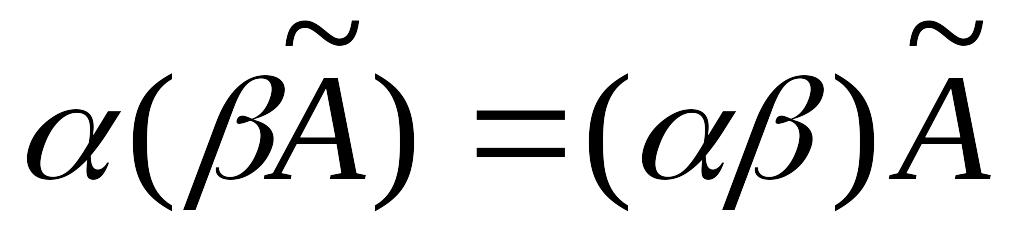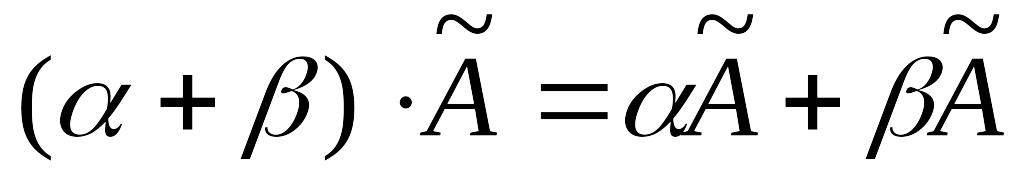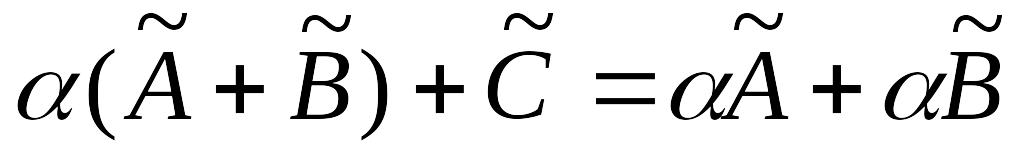3. ;

4. ;

5. .

3

Рис. 8

. Умножение линейных операторов. Рассмотрим оператор , переводящий вектор в вектор ., т.е. (см. рис. 8). К вектору применим оператор , переводящий вектор в вектор , т.е. . Таким образом, имеем оператор , переводящий вектор в вектор , причем вектор получен в результате последовательного применения операторов и .

Определение. Произведением линейных операторов и называется оператор , заключающийся в последовательном применении операторов и и определяемый равенством: (справа записывается первый оператор).

Произведение линейных операторов является линейным оператором:

;

.

Свойства операции умножения линейных операторов:

1. ;

2. ;

3. ;

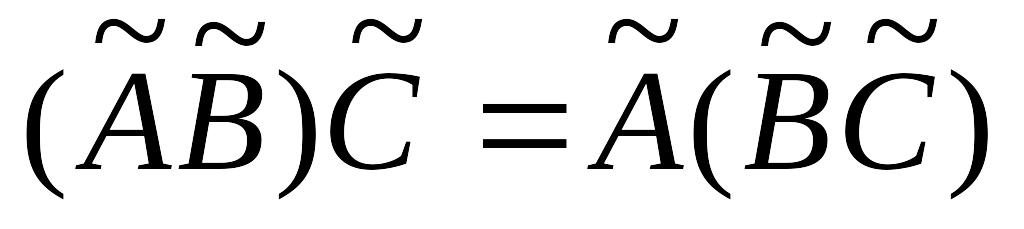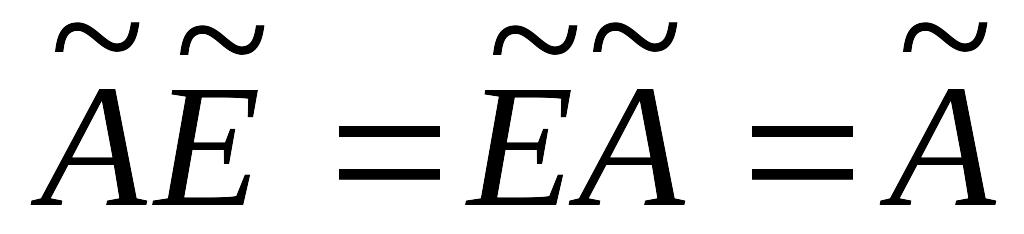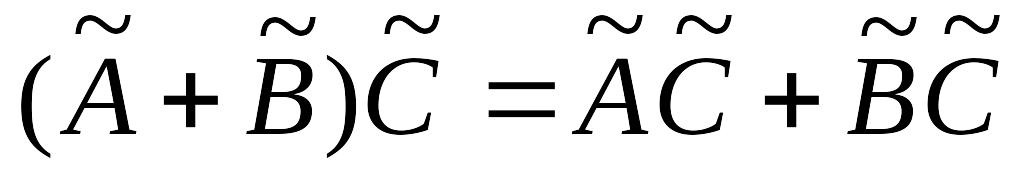Имеет место следующий принцип: каждому действию над линейными операторами соответствует такое же действие над матрицами этих линейных операторов.

Пример. Даны два линейных преобразования:

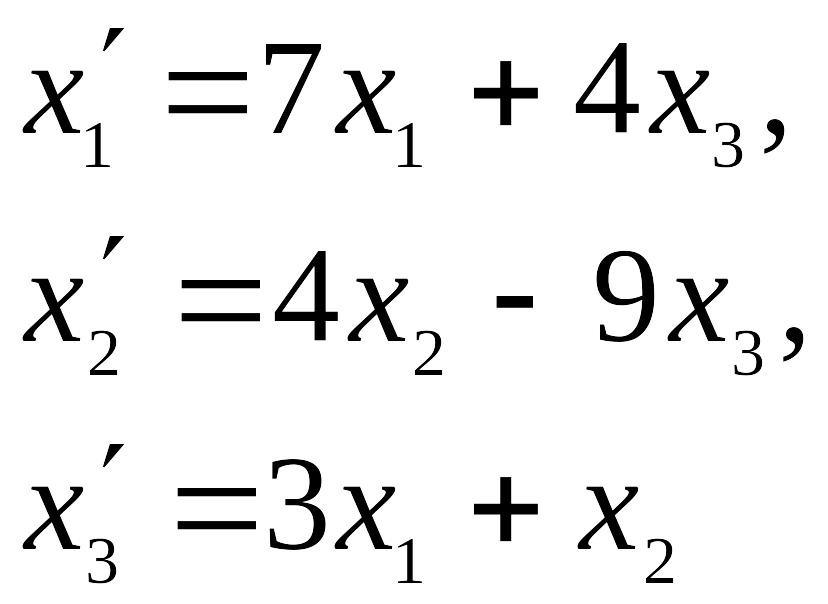
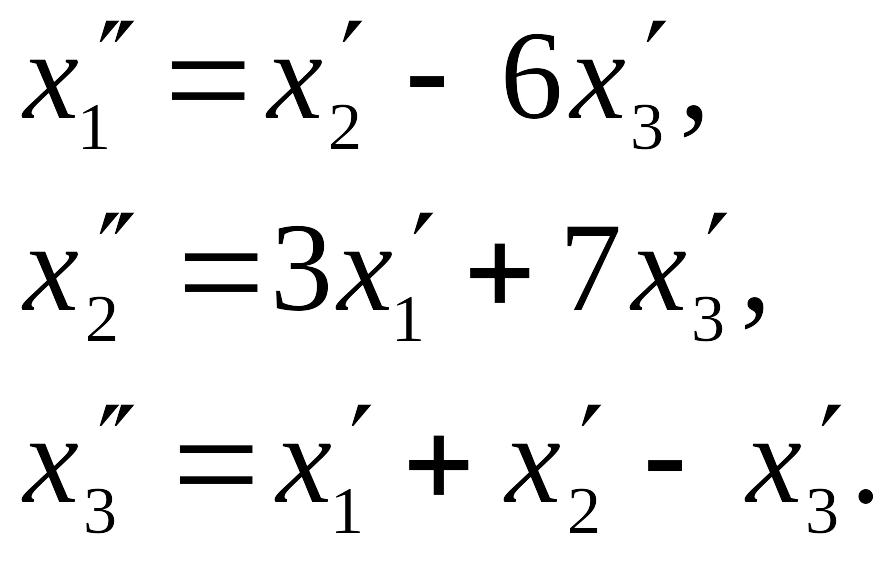
Средствами матричного исчисления найти преобразование, выражающее через .

Решение.

Первое преобразование задано матрицей А, второе – матрицей В:

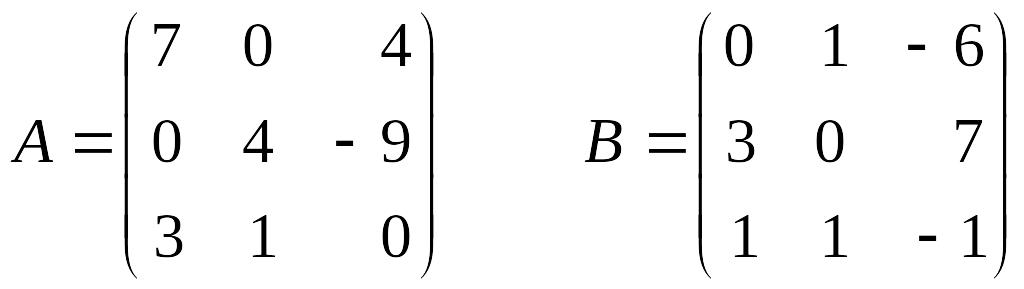
Искомое преобразование имеет матрицу ВА. Умножая матрицы В и А, получим:

Следовательно, искомое преобразование определяется формулами

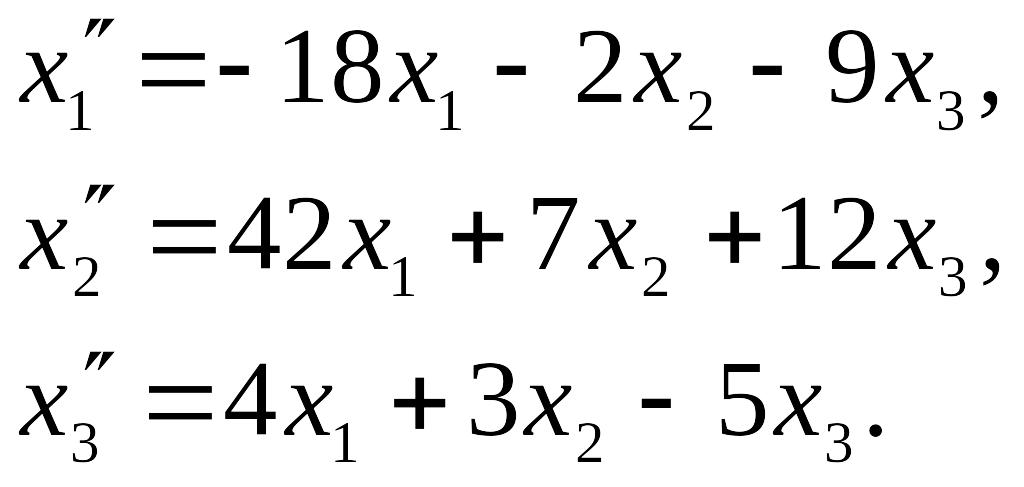
Операторы , λ , , полученные в результате арифметических действий, удовлетворяют отмеченным выше свойствам аддитивности и однородности, т.е. являются линейными.

9.5. Оператор, сопряженный данному

Рассмотрим линейный оператор , действующий в конечномерном линейном пространстве Rⁿ.

При фиксированном векторе скалярное произведение линейно относительно :

;

.:

Найдется такой вектор из линейного пространства Rⁿ, что при всех будет выполняться равенство: .

Этот вектор зависит только от и поэтому можно записать . Вектор определяется вектором , т.е. - оператор, переводящий вектор в вектор .

Покажем, что этот оператор линейный. Действительно, при любых выполняются условия:

Определение. Линейный оператор называется сопряженным оператору , если для любых двух векторов линейного пространства Rⁿ выполняется следующее условие:

.

Каждому линейному оператору соответствует единственный линейный сопряженный оператор .

Свойства оператора, сопряженного данному:

1. ;

2. ;

3. ;

4. ;

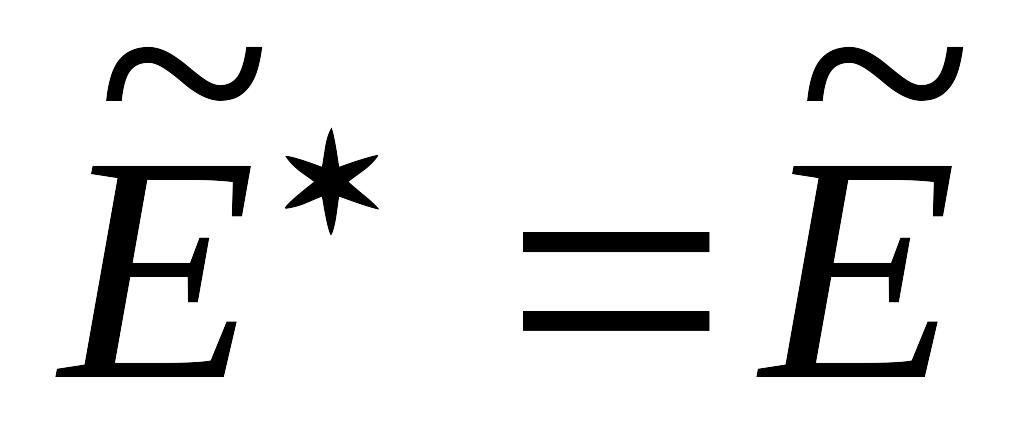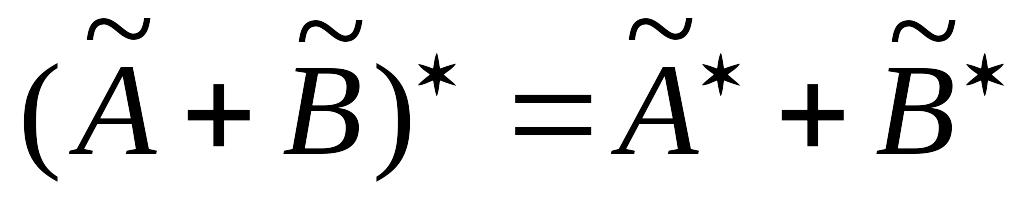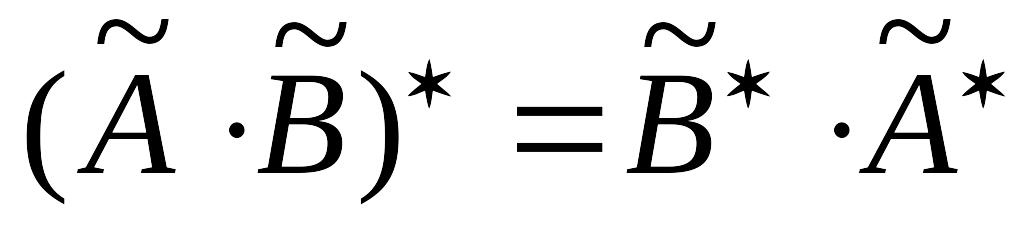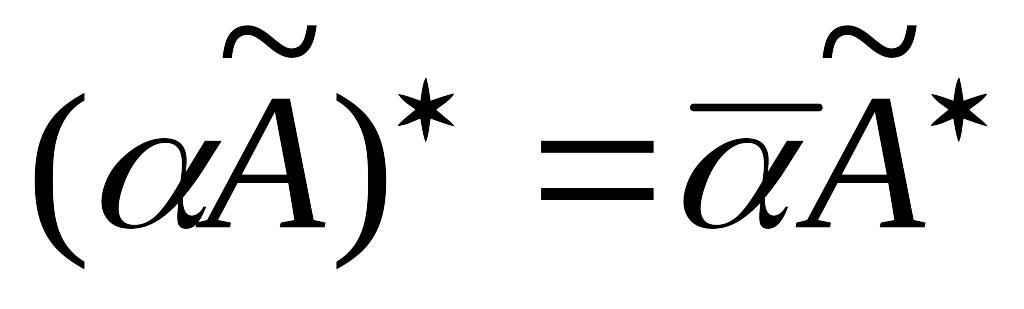5. если 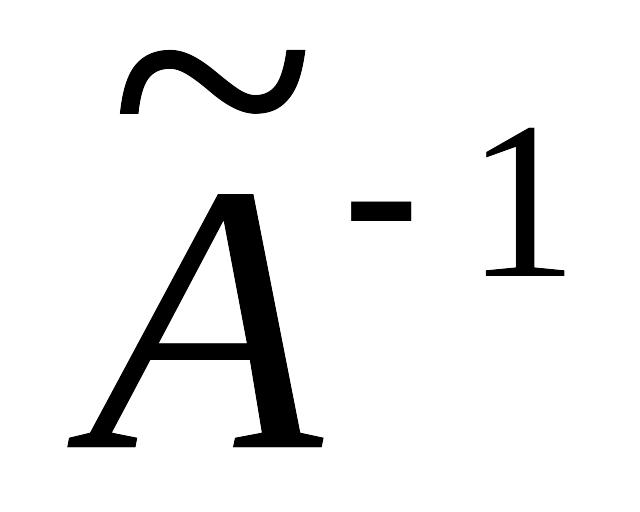существует, то .

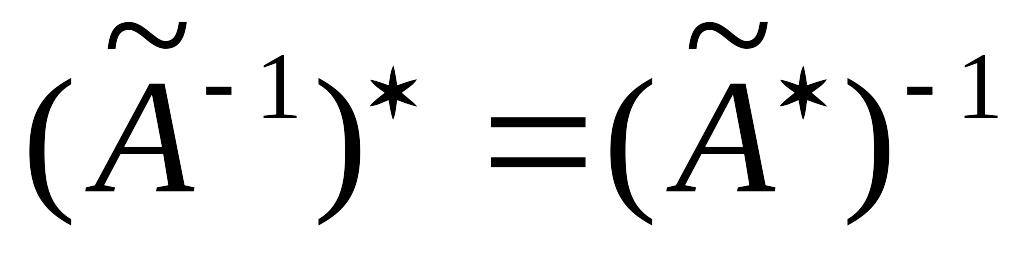Определение. Линейный оператор , совпадающий со своим сопряженным, т.е. такой, что , называется самосопряженным.

Таким образом, если - сопряженный оператор, то для любых двух векторов линейного пространства Rⁿ выполняется следующее условие:

.

Свойства самосопряженного оператора:

1. тождественный оператор является самосопряженным оператором: ;

2. сумма самосопряженных операторов является самосопряженной оператором

;

3. для того чтобы произведение самосопряженных операторов являлось самосопряженным оператором, необходимо и достаточно, чтобы эти операторы были перестановочны между собой

;

4. оператор, обратный к невырожденному самосопряженному оператору, является самосопряженным

;

5. если – сопряженный оператор, то для того чтобы произведение было самосопряженным оператором, необходимо и достаточно, чтобы число α было действительным: .
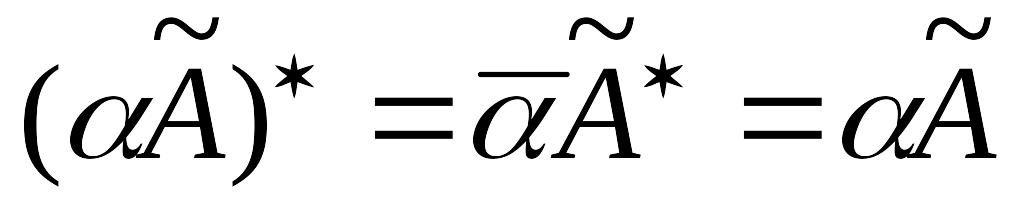