8.6. Системы линейных однородных уравнений (ослу)

Определение. Система m линейных уравнений с n переменными называется однородной, если все ее свободные члены равны нулю:

.

В матричной форме систему можно представить в виде: .

Система линейных однородных уравнений всегда совместна, так как всегда имеет, по крайней мере, одно тривиальное решение (нулевое). Этот же вывод можно сделать и из теоремы Кронекера-Капелли, так как добавление столбца из нулей не может повысить ранга матрицы.

Теорема (критерий наличия ненулевого решения ОСЛУ). Однородная система линейных уравнений иметь ненулевое решение тогда и только тогда, когда ранг системы меньше числа неизвестных.

Доказательство. Пусть ОСЛУ имеет ненулевое решение. Тогда она неопределенна и, следовательно, r<n. ■

Следствие 1. Если число уравнений ОСЛУ меньше числа неизвестных, то она имеет ненулевые решения.

Доказательство. Действительно, , m – число уравнений. Так как m<n, то r<n и ОСЛУ имеет ненулевые решения. ■

Следствие 2. Однородная система n линейных уравнений с n неизвестными имеет ненулевые решения тогда и только тогда, когда определитель этой системы равен нулю.

Доказательство. Действительно, пусть . Это означает, что единственный минор n-го порядка матрицы системы равен нулю и, в силу теоремы о ранге матрицы, r<n и ОСЛУ имеет ненулевые решения. ■

Если в системе линейных уравнений m= n , а ее определитель отличен от нуля, то такая система имеет только нулевое решение.

Пусть ранг системы r(A)=r. Далее будем рассматривать ОСЛУ с r<n. Решение системы запишем в виде вектора пространства Kⁿ: .

Множество таких решений обозначим . и - два произвольных решения системы.

Теорема (свойства решений ОСЛУ).

.

Доказательство. 1) Пусть и - два решения системы. Таким образом, и , - справедливые равенства.

Рассмотрим вектор . Проверим, что является решением однородной системы. Подставим его в систему:

.

2) Пусть . Рассмотрим вектор . Подставим его в систему: . ■

Следствие 3. Любая линейная комбинация решений ОСЛУ является решением этой системы.

Интересно найти такие линейно независимые решения системы, через которые линейно выражались бы все остальные ее решения.

Определение. Линейно независимая система решений (векторов) е₁, е₂,…, е_n-r называется фундаментальной (ФСР) если каждое решение системы линейных однородных уравнений является линейной комбинацией этих векторов.

Определение. Фундаментальной системой решений (ФСР) ОСЛУ называется любой базис множества Е всех решений этой системы.

Теорема (о фундаментальной системе решений). Если ранг ОСЛУ меньше числа неизвестных, то ФСР существует и число решений в любой из них равно n-r.

Если ранг системы r(A)= r, r<n; то система имеет n-r линейно независимых решений е₁,е₂,…е_n-r , причем любое решение системы является линейной комбинацией решений е₁,е₂,…е_n-r .

Правило нахождения фср ослу

Решение фундаментальной системы решений находят следующим образом:

– находят общее решение ОСЛУ;

– r базисных (основных) переменных х₁,х₂,…х_r выражают через свободные (неосновные) переменные;

– поочередно заменяют n-r свободных переменных элементами каждой строки невырожденной квадратной матрицы порядка n-r, например, единичной Е_n-r.

– объединяя значения для свободных и базисных переменных, получаем ФСР.

Следствие 4. Если набор решений е₁,е₂,…е_n-r. – ФСР ОСЛУ, то общее решение этой системы может быть записано в виде:

.

где с₁, с₂,с_n-r – произвольные числа поля K.

Пример. Найти общее решение и фундаментальную систему решений однородной системы уравнений:

Решение.

Выпишем матрицу системы, поставив последнее уравнение на первое место, затем приведем ее к ступенчатому виду:

.

Ранг матрицы r(A)= 2. Базисный минор при переменных х₁ и х₂ отличен от нуля . Выбираем в качестве основных переменных х₁ и х₂ и выражаем их через х₃ , х₄ и х₅:

.

Для получения фундаментальной системой решений е₁, е₂,…, е₃ поочередно заменяем неосновные переменные х₃, х₄ и х₅ элементами строк единичной матрицы Е₃.

При х₃=1 , х₄=0 и х₅=0 система примет вид:

, откуда , т.е. получили базисное решение .

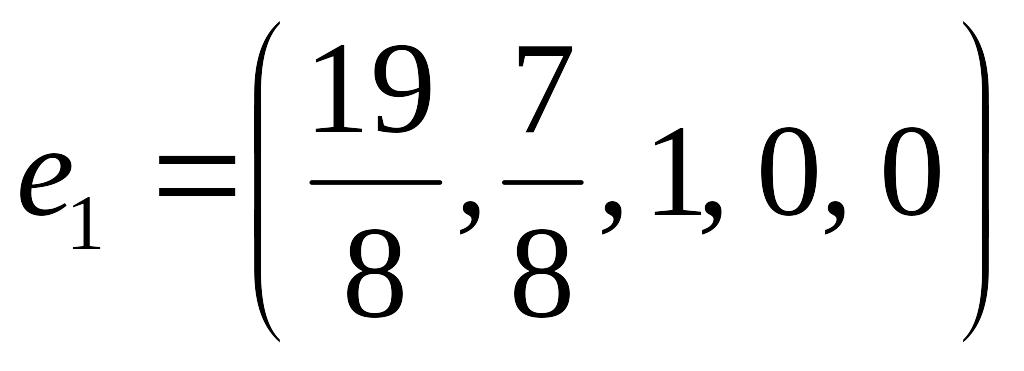При х₃=0 , х₄=1 и х₅=0 система примет вид:

, откуда , т.е. получили базисное решение .

При х₃=0 , х₄=0 и х₅=1 система примет вид:

, откуда , т.е. получили базисное решение . Найденные решения (векторы) е₁, е₂,…, е₃ образуют фундаментальную систему. Тогда общее решение системы имеет вид: