Правило нахождения решения слу в общем случае

Для решения совместной СЛУ ранга r необходимо:

1. найти любой базисный минор матрицы исходной системы и выписать соответствующую ему базисную подсистему;

2. свободные неизвестные перенести вправо и объявить их параметрами;

3. решить полученную систему r линейных уравнений с r неизвестными и получить общее решение СЛУ.

Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, так называемые системы крамеровского типа.

8.4. Решение систем n линейных уравнений c n неизвестными

Рассмотрим систему n линейных уравнений с n неизвестными:

.

Определение. Система линейных уравнений называется квадратной, если число уравнений системы рано числу неизвестных этой системы, т.е. m=n.

Определение. Определителем ∆ системы n линейных уравнений c n неизвестными называется определитель, порожденный матрицей этой системы

.

Определение. Вспомогательным (дополнительным) определителем системы называется определитель ∆_i, получающийся из определителя ∆ заменой i-го столбца столбцом свободных членов этой системы

.

Определение. Квадратная система линейных уравнений называется невырожденной, если определитель ее системы отличен от нуля.

Квадратные СЛУ решаются одним из следующих способов:

1. методом Крамера;

2. методом обратной матрицы;

3. методом Гаусса.

8.4.1. Решение систем n линейных уравнений c n неизвестными методом Крамера

Теорема Крамера. Если определитель D системы n линейных уравнений c n неизвестными отличен от нуля, то система совместна и определена и ее единственное решение определяется по формулам

.

Доказательство. Ясно, что для любой системы m линейных уравнений c n неизвестными выполняются неравенства . Мы рассматриваем случай m =n, поэтому получаем , т.е. . Так как по условию теоремы определитель системы , то по теореме о ранге матрицы получаем , поэтому возможно только если . Равенство означает совместность нашей системы, а - ее определенность.

Пусть - единственное решение системы. Подставим его во все уравнения системы. Получим верные числовые равенства

.

Через обозначим алгебраическое дополнение элемента определителя ∆. Зафиксируем число и i –е числовое равенство умножим на :

.

Просуммируем все такие равенства по i:

.

Учитывая, что , где - символ Кронекера, получаем

. ■

Если определитель системы и все вспомогательные определители равны нулю, то система имеет бесчисленное множество решений. Если же определитель системы , а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.

Пример:

,

Решение.

,

, следовательно, система имеет решение.

, .

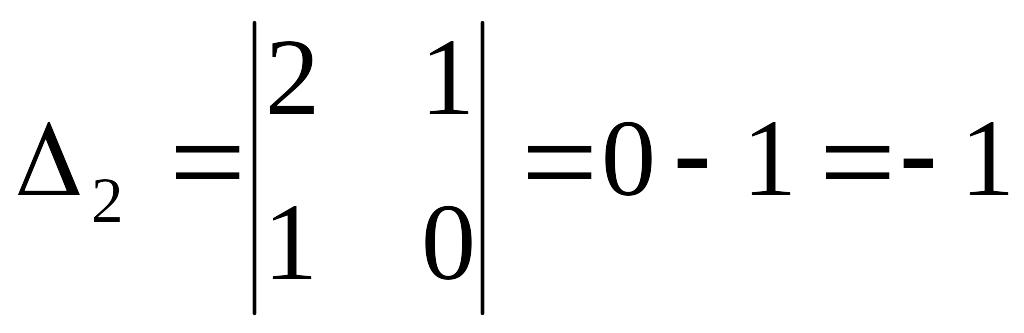Тогда

, .

Получили решение системы: .

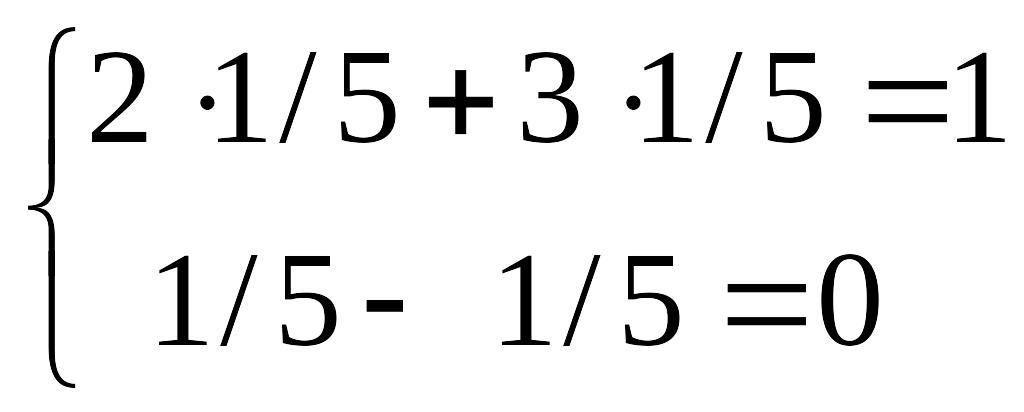
Проверка: . Решение верно.

8.4.2. Решение систем n линейных уравнений c n неизвестными методом обратной матрицы

Теорема. Если в СЛУ квадратная матрица системы невырождена, то система уравнений имеет единственное решение, равное вектору

.

Доказательство. Так как по условию матрица системы невырождена, т.е. , то матрица А обратима. Умножая слева обе части матричного уравнения на матрицу , получим:

. ■

Пример. Методом обратной матрицы решить систему уравнений:

Решение.

Перепишем исходную систему в матричной форме АХ=В, где:

, .

Определитель матрицы , таким образом, обратная матрица существует и равна .

Определим вектор Х по формуле :

. Получили решение системы: