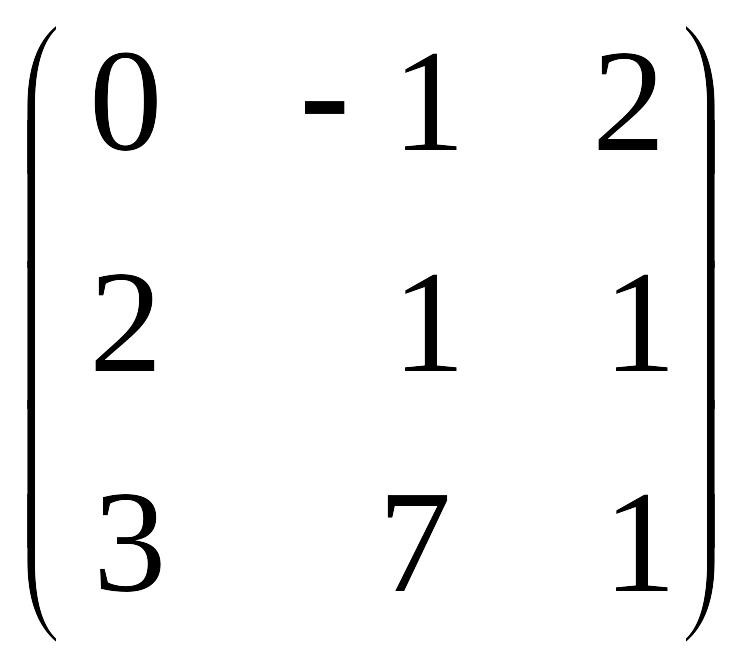- •Математика Линейная алгебра
- •Рецензенты:
- •3.6. Операции над векторами 42
- •5.6. Упражнения 91
- •Предисловие
- •1. Числовые кольца и поля. Комплексные числа
- •1.1. Основные понятия
- •1.2. Поле комплексных чисел
- •1.3. Модуль и аргумент комплексного числа. Геометрическое изображение комплексных чисел
- •1.4. Различные формы записи комплексного числа
- •1.5. Действия над комплексными числами в алгебраической форме
- •1.6. Действия над комплексными числами в тригонометрической форме
- •1.7. Действия над комплексными числами в показательной форме
- •1.8. Упражнения
- •1.9. Контрольные задания
- •1.10. Типовой расчет
- •1.11. Вопросы для самопроверки
- •1.12. Вопросы для теоретического опроса
- •2. Многочлены
- •2.1. Действия над многочленами
- •1. Сложение многочленов.
- •2. Умножение многочленов.
- •3. Деление многочленов без остатка.
- •4. Деление многочленов с остатком.
- •2.2. Схема Горнера
- •2.3. Корни многочлена
- •2.3.1. Разложение многочлена степени n на множители
- •2.3.2. Вычисление корней многочленов второй и третьей степени
- •1. Уравнения второй степени (квадратные)
- •2.4. Упражнения
- •2.5. Контрольные задания
- •2.6. Вопросы для самопроверки
- •2.7. Вопросы для теоретического опроса
- •Действия над многочленами.
- •Вычисление корней многочленов второй и третьей степени.
- •3. Линейные (векторные) пространства
- •3.1. Понятие вектора
- •3.2. Операции над векторами
- •1. Операция сложения векторов.
- •2. Операция вычитания векторов.
- •3. Умножение вектора на число.
- •4. Деление коллинеарных векторов.
- •Свойства деления:
- •3.3. Разложение вектора по ортам координатных осей
- •3.4. Скалярное произведение векторов.
- •Выражение скалярного произведения в произвольных и ортонормированных координатах.
- •3.6. Операции над векторами
- •3.7. Линейная зависимость векторов.
- •3.8. Базис и ранг системы векторов
- •3.9. Переход от одного базиса к другому. Метод замещения
- •3.10. Линейные пространства
- •3.11. Евклидовы и унитарные пространства
- •3.12. Норма вектора
- •3.13. Нормирование ненулевого вектора
- •3.14. Ортонормированные системы векторов
- •3.15. Упражнения
- •3.16. Контрольные задания
- •3.17. Типовой расчет
- •3.18. Вопросы для самопроверки
- •3.19. Вопросы для теоретического опроса
- •Переход от одного базиса к другому. Метод замещения.
- •Ортонормированные системы векторов.
- •4. Матрицы
- •4.1. Основные понятия
- •4.2 Операции над матрицами
- •Сложение матриц.
- •Умножение матрицы на число.
- •Разность матриц.
- •Умножение матриц.
- •Возведение в степень матриц.
- •Транспонирование матриц.
- •4.3. Применение элементов линейной алгебры в экономике.
- •4.4. Упражнения
- •4.5. Контрольные задания
- •Найти значение матричного многочлена , если задана матрица a.
- •4.6. Типовой расчет
- •4.7. Вопросы для самопроверки
- •4.8. Вопросы для теоретического опроса
- •5. Определители квадратных матриц
- •5.1. Перестановки
- •5.2. Определители (детерминанты) квадратных матриц
- •5.3. Свойства определителей
- •5.4. Теорема Лапласа (вычисление определителя n-ого порядка).
- •5.5. Основные методы вычисления определителя n–го порядка
- •Приведение определителя к треугольному виду.
- •5.6. Упражнения
- •5.7. Контрольные задания
- •5.8. Типовой расчет
- •5.9. Вопросы для самопроверки
- •5.10. Вопросы для теоретического опроса
- •6. Ранг матрицы
- •6.1. Основные понятия
- •6.2. Методы нахождения ранга матрицы.
- •1. Метод окаймляющих миноров
- •2. Метод элементарных преобразований
- •6.3. Упражнения
- •6.4. Контрольные задания
- •6.5. Типовой расчет
- •6.6. Вопросы для самопроверки
- •6.7. Вопросы для теоретического опроса
- •7. Обратная матрица
- •7.1. Основные понятия
- •7.2. Методы нахождения обратной матрицы
- •7.2.1. Нахождение обратной матрицы с помощью присоединенной матрицы.
- •7.2.2. Нахождение обратной матрицы методом замещения
- •7.3. Упражнения
- •7.4. Контрольные задания
- •7.5. Типовой расчет
- •7.6. Вопросы для самопроверки
- •7.7. Вопросы для теоретического опроса
- •Нахождение обратной матрицы с помощью присоединенной матрицы.
- •Нахождение обратной матрицы методом замещения.
- •8. Системы линейных уравнений (слу)
- •8.1. Неоднородные системы уравнений
- •8.2. Исследование систем линейных уравнений
- •8.3. Решение системы линейных уравнений в общем случае
- •Правило нахождения решения слу в общем случае
- •8.4. Решение систем n линейных уравнений c n неизвестными
- •8.4.1. Решение систем n линейных уравнений c n неизвестными методом Крамера
- •8.4.2. Решение систем n линейных уравнений c n неизвестными методом обратной матрицы
- •8.5. Решение систем m линейных уравнений c n неизвестными
- •8.5.1. Решение систем линейных уравнений методом Гаусса (метод последовательного исключения неизвестных)
- •8.5.2. Решение систем линейных уравнений методом замещения
- •8.6. Системы линейных однородных уравнений (ослу)
- •Правило нахождения фср ослу
- •8.7. Структура общего решения неоднородной линейной системы
- •8.8. Использование систем линейных уравнений в экономике
- •8.8.1. Прогноз выпуска продукции по запасам сырья
- •8.8.2. Модель Леонтьева многоотраслевой экономики (балансовый анализ) Балансовые соотношения
- •Линейная модель межотраслевой экономики
- •Продуктивные модели Леонтьева
- •8.9. Упражнения
- •8.10. Контрольные задания
- •8.11. Типовой расчет
- •8.12. Вопросы для самопроверки
- •8.13. Вопросы для теоретического опроса
- •9. Линейные операторы (линейные преобразования)
- •9.1. Линейный оператор и его матрица
- •9.2. Линейное преобразование в координатах
- •9.3. Зависимость между матрицами одного и того же преобразования в различных базисах. Подобные матрицы
- •9.4. Действия над линейными операторами
- •9.5. Оператор, сопряженный данному
- •9.6. Собственные значения и собственные векторы линейного оператора (матрицы)
- •9.7. Приведение матрицы линейного преобразования к диагональному виду
- •9.8. Упражнения
- •9.9. Контрольные задания
- •9.10. Типовой расчет
- •9.11. Вопросы для самопроверки
- •9.12. Вопросы для теоретического опроса
- •10. Билинейные и квадратичные формы
- •10.1 Ортогональные и симметрические матрицы
- •10.2. Билинейная и квадратичная формы
- •10.3. Квадратичные формы
- •10.4. Преобразование квадратичной формы при линейном преобразовании переменных
- •10.5. Приведение квадратичной формы к каноническому виду
- •10.6. Закон инерции квадратичных форм
- •10.7. Знакоопределенные квадратичные формы
- •10.8. Упражнения
- •10.9. Контрольные задания
- •10.5. Вопросы для самопроверки
- •10.6. Вопросы для теоретического опроса
- •11. Численные методы линейной алгебры
- •11.1. Метод Гаусса
- •11.2. Уточнение решения методом итераций
- •11.3. Метод прогонки
- •11.4. Итерационные методы решения слау
- •11.4.1. Метод простой итерации
- •11.4.2. Метод Зейделя
- •11.5. Упражнения
- •11.6. Контрольные задания
- •11.7. Типовой расчет
- •11.8. Вопросы для самопроверки
- •11.9. Вопросы для теоретического опроса
7.3. Упражнения
Найти матрицу А-1 , обратную матрице А, если:
а)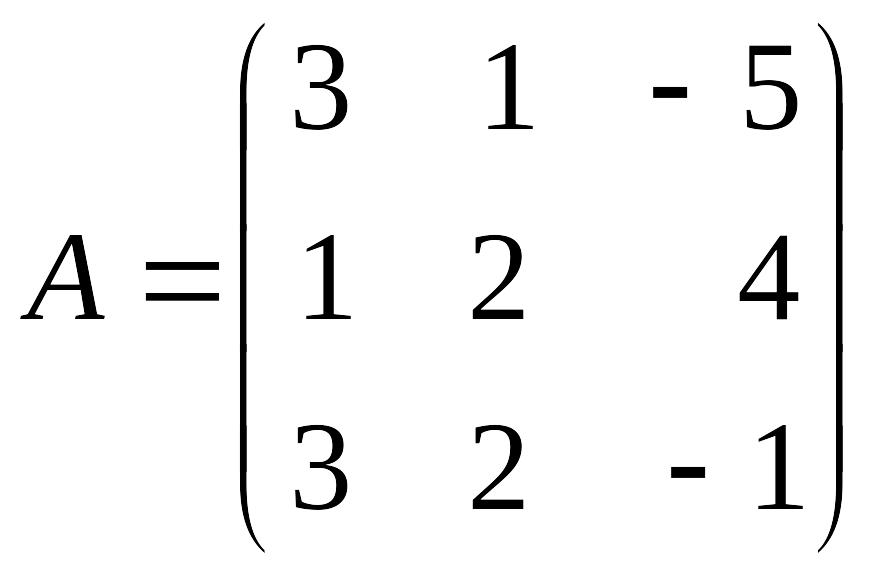 Ответ:
Ответ:
 ;
;
б)
 Ответ:
Ответ:
 ;
;
в)
 Ответ:
Ответ:
 .
.
7.4. Контрольные задания
Найти обратную матрицу A-1 с помощью присоединенной матрицы и метода замещения. Проверить правильность вычислений по формуле
AA-1=A-1A=E.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7.5. Типовой расчет
Дана
матрица
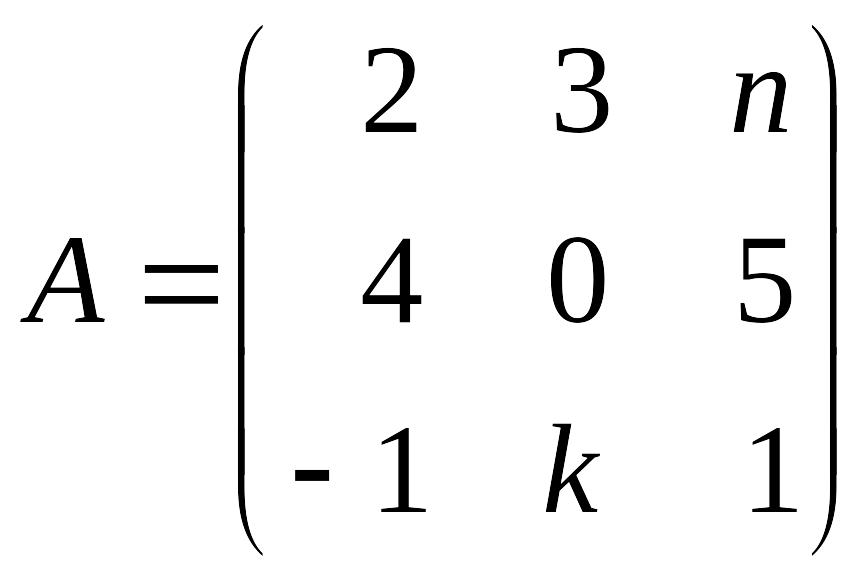 ,
где n
– номер студента в групповом журнале,
а k
– номер группы студента.
,
где n
– номер студента в групповом журнале,
а k
– номер группы студента.
Найти обратную матрицу A-1: 1)с помощью присоединенной матрицы; 2)методом замещения. Сделать проверку: AA-1=E.
7.6. Вопросы для самопроверки
Какая матрица называется обратной по отношению к матрице А?
Какая матрица называется обратимой?
Укажите свойства обратных матриц.
Какая матрица называется невырожденной?
Какую матрицу называют присоединенной для матрицы А?
Укажите методы нахождения обратной матрицы.
Каково условие существования обратной матрицы?
Сформулируйте теорему об обратимости матриц.
Нахождение обратной матрицы
Изложите алгоритм нахождения обратной матрицы с помощью присоединенной матрицы.
Изложите алгоритм нахождения обратной матрицы методом замещения.
Что вычисляется с помощью правила прямоугольника?
7.7. Вопросы для теоретического опроса
Понятия обратной и обратимой матриц. Свойства обратных матриц.
Невырожденная матрица. Теорема об обратимости матриц.
Присоединенная матрица. Теорема о присоединенной матрице.
Нахождение обратной матрицы с помощью присоединенной матрицы.
Нахождение обратной матрицы методом замещения.
8. Системы линейных уравнений (слу)
8.1. Неоднородные системы уравнений
Определение. Алгебраическое выражение:
![]() ,
,
содержащее неизвестные
![]() в первой степени, называется линейным
уравнением.
в первой степени, называется линейным
уравнением.
Определение. Системой m линейных уравнений с n неизвестными называется совокупность уравнений вида
 ,
,
где
![]() и
и
![]() (
(![]() )
– произвольные числа, называемые
соответственно коэффициентами
при неизвестных
и
свободными
членами.
)
– произвольные числа, называемые
соответственно коэффициентами
при неизвестных
и
свободными
членами.
Определение. Система называется неоднородной, если хотя бы один из ее свободных членов отличен от нуля.
Таким образом, система вида
является неоднородной.
Систему уравнений можно представить и в более краткой записи:
![]()
Любую систему линейных уравнений можно записать в виде матричного уравнения вида . Для этого введем в рассмотрение следующие матрицы:
 ,
, 
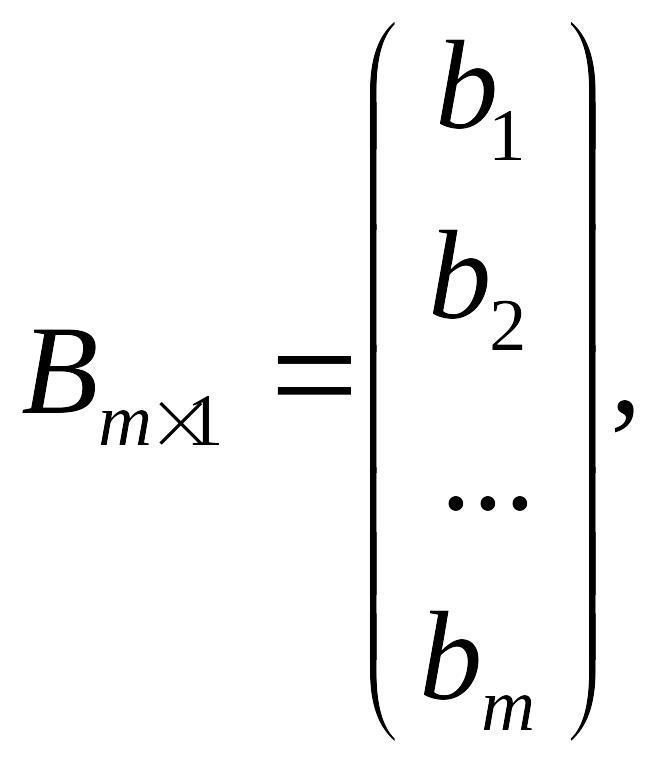
где А – матрица из коэффициентов при неизвестных, называемая основной матрицей системы , X – столбец неизвестных, B – столбец свободных членов.
Записывая систему уравнений в векторной форме введем обозначения для столбцов матрицы А:
 ,
, ,…,
,…, .
.
Тогда система линейных уравнений в векторной форме имеет вид
![]()
Определение. Решением
системы называется упорядоченная
совокупность n чисел
![]() ,
при подстановке которых все уравнения
системы обращаются в тождества.
,
при подстановке которых все уравнения
системы обращаются в тождества.
Решение системы можно рассматривать как вектор пространства Kn.
Ясно, что вектор будет решением тогда и только и тогда, когда выполняется векторное равенство
![]() .
.
Определение. Если система уравнений имеет хотя бы одно решение, то она называется совместной, и несовместной (противоречивой), если эта система не имеет решений.
Определение. Совместная система линейных уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Определение. Две системы линейных уравнений с одним и тем же числом неизвестных называются эквивалентными (равносильными), если множества их решений совпадают.
Определение. Преобразования системы уравнений называются элементарными, если они не изменяют множества решений системы.
К ним относятся:
умножение обеих частей какого-либо уравнения системы на число, не равное нулю;
замена i-го уравнения СЛУ, которая получается путем сложения прибавление к обеим частям i-го уравнения соответствующих частей j-го уравнения, умноженного на число, отличное от нуля.