
- •Математика Линейная алгебра
- •Рецензенты:
- •3.6. Операции над векторами 42
- •5.6. Упражнения 91
- •Предисловие
- •1. Числовые кольца и поля. Комплексные числа
- •1.1. Основные понятия
- •1.2. Поле комплексных чисел
- •1.3. Модуль и аргумент комплексного числа. Геометрическое изображение комплексных чисел
- •1.4. Различные формы записи комплексного числа
- •1.5. Действия над комплексными числами в алгебраической форме
- •1.6. Действия над комплексными числами в тригонометрической форме
- •1.7. Действия над комплексными числами в показательной форме
- •1.8. Упражнения
- •1.9. Контрольные задания
- •1.10. Типовой расчет
- •1.11. Вопросы для самопроверки
- •1.12. Вопросы для теоретического опроса
- •2. Многочлены
- •2.1. Действия над многочленами
- •1. Сложение многочленов.
- •2. Умножение многочленов.
- •3. Деление многочленов без остатка.
- •4. Деление многочленов с остатком.
- •2.2. Схема Горнера
- •2.3. Корни многочлена
- •2.3.1. Разложение многочлена степени n на множители
- •2.3.2. Вычисление корней многочленов второй и третьей степени
- •1. Уравнения второй степени (квадратные)
- •2.4. Упражнения
- •2.5. Контрольные задания
- •2.6. Вопросы для самопроверки
- •2.7. Вопросы для теоретического опроса
- •Действия над многочленами.
- •Вычисление корней многочленов второй и третьей степени.
- •3. Линейные (векторные) пространства
- •3.1. Понятие вектора
- •3.2. Операции над векторами
- •1. Операция сложения векторов.
- •2. Операция вычитания векторов.
- •3. Умножение вектора на число.
- •4. Деление коллинеарных векторов.
- •Свойства деления:
- •3.3. Разложение вектора по ортам координатных осей
- •3.4. Скалярное произведение векторов.
- •Выражение скалярного произведения в произвольных и ортонормированных координатах.
- •3.6. Операции над векторами
- •3.7. Линейная зависимость векторов.
- •3.8. Базис и ранг системы векторов
- •3.9. Переход от одного базиса к другому. Метод замещения
- •3.10. Линейные пространства
- •3.11. Евклидовы и унитарные пространства
- •3.12. Норма вектора
- •3.13. Нормирование ненулевого вектора
- •3.14. Ортонормированные системы векторов
- •3.15. Упражнения
- •3.16. Контрольные задания
- •3.17. Типовой расчет
- •3.18. Вопросы для самопроверки
- •3.19. Вопросы для теоретического опроса
- •Переход от одного базиса к другому. Метод замещения.
- •Ортонормированные системы векторов.
- •4. Матрицы
- •4.1. Основные понятия
- •4.2 Операции над матрицами
- •Сложение матриц.
- •Умножение матрицы на число.
- •Разность матриц.
- •Умножение матриц.
- •Возведение в степень матриц.
- •Транспонирование матриц.
- •4.3. Применение элементов линейной алгебры в экономике.
- •4.4. Упражнения
- •4.5. Контрольные задания
- •Найти значение матричного многочлена , если задана матрица a.
- •4.6. Типовой расчет
- •4.7. Вопросы для самопроверки
- •4.8. Вопросы для теоретического опроса
- •5. Определители квадратных матриц
- •5.1. Перестановки
- •5.2. Определители (детерминанты) квадратных матриц
- •5.3. Свойства определителей
- •5.4. Теорема Лапласа (вычисление определителя n-ого порядка).
- •5.5. Основные методы вычисления определителя n–го порядка
- •Приведение определителя к треугольному виду.
- •5.6. Упражнения
- •5.7. Контрольные задания
- •5.8. Типовой расчет
- •5.9. Вопросы для самопроверки
- •5.10. Вопросы для теоретического опроса
- •6. Ранг матрицы
- •6.1. Основные понятия
- •6.2. Методы нахождения ранга матрицы.
- •1. Метод окаймляющих миноров
- •2. Метод элементарных преобразований
- •6.3. Упражнения
- •6.4. Контрольные задания
- •6.5. Типовой расчет
- •6.6. Вопросы для самопроверки
- •6.7. Вопросы для теоретического опроса
- •7. Обратная матрица
- •7.1. Основные понятия
- •7.2. Методы нахождения обратной матрицы
- •7.2.1. Нахождение обратной матрицы с помощью присоединенной матрицы.
- •7.2.2. Нахождение обратной матрицы методом замещения
- •7.3. Упражнения
- •7.4. Контрольные задания
- •7.5. Типовой расчет
- •7.6. Вопросы для самопроверки
- •7.7. Вопросы для теоретического опроса
- •Нахождение обратной матрицы с помощью присоединенной матрицы.
- •Нахождение обратной матрицы методом замещения.
- •8. Системы линейных уравнений (слу)
- •8.1. Неоднородные системы уравнений
- •8.2. Исследование систем линейных уравнений
- •8.3. Решение системы линейных уравнений в общем случае
- •Правило нахождения решения слу в общем случае
- •8.4. Решение систем n линейных уравнений c n неизвестными
- •8.4.1. Решение систем n линейных уравнений c n неизвестными методом Крамера
- •8.4.2. Решение систем n линейных уравнений c n неизвестными методом обратной матрицы
- •8.5. Решение систем m линейных уравнений c n неизвестными
- •8.5.1. Решение систем линейных уравнений методом Гаусса (метод последовательного исключения неизвестных)
- •8.5.2. Решение систем линейных уравнений методом замещения
- •8.6. Системы линейных однородных уравнений (ослу)
- •Правило нахождения фср ослу
- •8.7. Структура общего решения неоднородной линейной системы
- •8.8. Использование систем линейных уравнений в экономике
- •8.8.1. Прогноз выпуска продукции по запасам сырья
- •8.8.2. Модель Леонтьева многоотраслевой экономики (балансовый анализ) Балансовые соотношения
- •Линейная модель межотраслевой экономики
- •Продуктивные модели Леонтьева
- •8.9. Упражнения
- •8.10. Контрольные задания
- •8.11. Типовой расчет
- •8.12. Вопросы для самопроверки
- •8.13. Вопросы для теоретического опроса
- •9. Линейные операторы (линейные преобразования)
- •9.1. Линейный оператор и его матрица
- •9.2. Линейное преобразование в координатах
- •9.3. Зависимость между матрицами одного и того же преобразования в различных базисах. Подобные матрицы
- •9.4. Действия над линейными операторами
- •9.5. Оператор, сопряженный данному
- •9.6. Собственные значения и собственные векторы линейного оператора (матрицы)
- •9.7. Приведение матрицы линейного преобразования к диагональному виду
- •9.8. Упражнения
- •9.9. Контрольные задания
- •9.10. Типовой расчет
- •9.11. Вопросы для самопроверки
- •9.12. Вопросы для теоретического опроса
- •10. Билинейные и квадратичные формы
- •10.1 Ортогональные и симметрические матрицы
- •10.2. Билинейная и квадратичная формы
- •10.3. Квадратичные формы
- •10.4. Преобразование квадратичной формы при линейном преобразовании переменных
- •10.5. Приведение квадратичной формы к каноническому виду
- •10.6. Закон инерции квадратичных форм
- •10.7. Знакоопределенные квадратичные формы
- •10.8. Упражнения
- •10.9. Контрольные задания
- •10.5. Вопросы для самопроверки
- •10.6. Вопросы для теоретического опроса
- •11. Численные методы линейной алгебры
- •11.1. Метод Гаусса
- •11.2. Уточнение решения методом итераций
- •11.3. Метод прогонки
- •11.4. Итерационные методы решения слау
- •11.4.1. Метод простой итерации
- •11.4.2. Метод Зейделя
- •11.5. Упражнения
- •11.6. Контрольные задания
- •11.7. Типовой расчет
- •11.8. Вопросы для самопроверки
- •11.9. Вопросы для теоретического опроса
Предисловие
Данное пособие разработано для студентов направления 080700.62 «Бизнес-информатика» и специальности 080116.65 «Математические методы в экономике» на основе государственных образовательных стандартов.
Цель пособия – оказать помощь студентам в изучении данной дисциплины, для организации их самостоятельной работы и подготовки к итоговому контролю.
Изучение линейной алгебры в данном пособии начинается с разделов «Числовые кольца и поля. Комплексные числа» и «Многочлены», которые продолжают школьный курс математики по этим темам. Раздел «Линейные векторные пространства» позволяет перейти на новый, более высокий, уровень при изучении «Линейной алгебры».
Последующие разделы пособия являются классическими для курса «Линейной алгебры».
Особенностью данного пособия является включение в него раздела «Численные методы линейной алгебры». Этот раздел содержит не только теоретические основы решения систем численными методами, но и блок-схемы алгоритмов, фрагменты программного кода, позволяющие студентам самостоятельно разрабатывать программы для решения систем уравнений, исследовать сходимость и устойчивость численных методов, а также оценивать ошибки полученного решения.
1. Числовые кольца и поля. Комплексные числа
1.1. Основные понятия
Понятие множества относится к числу простейших и в то же время фундаментальных понятий математики.
Определение. Множество – это совокупность каких-либо объектов произвольной природы, объединенных по определенному признаку.
Определение. Объекты, составляющие множество, называются его элементами или точками.
Множества обозначаются прописными буквами A, B, C, а входящие в них элементы — строчными a, b, c.
Выражение «элемент х из множества
X» кратко записывается в виде
![]() (х принадлежит X); если же элемент
х не является элементом множества
X, то это соответствует записи
(х принадлежит X); если же элемент
х не является элементом множества
X, то это соответствует записи
![]() (х не принадлежит X).
(х не принадлежит X).
Определение.
Множество,
состоящее из конечного числа элементов,
называется конечным,
а множество, состоящее из бесконечного
числа элементов – бесконечным.
Конечное множество можно задать
перечислением всех его элементов:
![]() .
.
Если число n достаточно велико, то множество задается с помощью характеристического свойства, т.е. свойства, которым обладает каждый элемент множества и не обладает ни один элемент, не принадлежащий этому множеству:
![]() ,
,
где Р(х) – характеристическое свойство множества Х.
Например,
![]() .
.
Введем некоторые обозначения.
Определение. Утверждение, относительно которого известно истинно оно или ложно, называется высказыванием.
Для краткой записи математических утверждений используются следующие логические символы (кванторы):
" – квантор общности заменяет слова «для любого», «для каждого», «для всех».
Вместо выражения
«любой элемент х
из множества X»
записывается:
![]() .
Например, выражение «"x:
Р(х)»
означает, что для любого
(каждого) х
имеет место Р(х).
.
Например, выражение «"x:
Р(х)»
означает, что для любого
(каждого) х
имеет место Р(х).
$ – квантор существования заменяет слова «существует», «найдется».
Вместо выражения
«существует элемент х из множества
X» кратко пишут:
![]() .
Например, выражение
«
.
Например, выражение
«![]() »
означает, что существует
(найдется) такой х,
что имеет место Р(х).
»
означает, что существует
(найдется) такой х,
что имеет место Р(х).
Þ – логический квантор следования (импликации).
Запись X Þ Y означает, что X следует из Y (X влечет за собой Y).
Û – логический квантор равносильности (эквивалентности).
Вместо
выражения «X
тогда и только
тогда, когда Y»
или «X эквивалентно Y»
кратко пишут:
![]() .
.
 (Ù)
– логический символ конъюнкции
(знак пересечения).
(Ù)
– логический символ конъюнкции
(знак пересечения).
Вместо выражения
«X и
Y»
кратко пишут:
![]() (XÙY).
(XÙY).
 (Ú)
– логический символ дизъюнкции
(знак объединения).
(Ú)
– логический символ дизъюнкции
(знак объединения).
Вместо выражения
«X или
Y»
или «хотя бы одно из X
или Y»
кратко пишут:
![]() (XÚY).
(XÚY).
Определение.
Если все элементы множества Х содержатся
в множестве Y, то Х целиком содержится
в Y, или
![]() (X является подмножеством
множества Y):
(X является подмножеством
множества Y):
![]() .
.
Определение.
Если ни один элемент множества Х не
содержится в Y, то, значит, и само множество
Х не содержится в Y, или
![]() (X не является подмножеством
множества Y):
(X не является подмножеством
множества Y):
![]() .
.
Определение. Пустым множеством называется множество, обозначаемое символом Æ, в котором не содержится ни одного элемента.
Пустое множество является подмножеством любого множества.
Определение. Множества, элементами которых являются числа, называются числовыми.
Для числовых множеств, которые часто применяются, вводятся специальные обозначения. К ним относятся:
N – множество всех натуральных чисел: 1, 2, 3…;
Z – множество всех целых чисел: …–2, –1, 0, 1, 2,…;
Q – множество всех рациональных
чисел, т.е. дробей вида
![]() (
(![]() );
);
R – множество всех действительных чисел, которое состоит из рациональных и иррациональных чисел;
С – множество всех комплексных чисел (данное множество мы рассмотрим ниже);
K – обозначение любого из перечисленных выше множеств (N, Z, Q, R, С).
Определение. Если два множества Х и Y состоят из одних и тех же элементов, то они называются равными, что соответствует записи Х=Y.
Запись
![]() означает, что множества X и Y не
равны друг другу, т.е. существует элемент,
принадлежащий одному из этих множеств
и не принадлежащий другому. Таким
образом,
означает, что множества X и Y не
равны друг другу, т.е. существует элемент,
принадлежащий одному из этих множеств
и не принадлежащий другому. Таким
образом,
![]() .
.
Пусть R – множество действительных чисел. Рассмотрим произвольное его подмножество KÌR.
Определение. Числовое множество K называется числовым кольцом, если оно содержит сумму, разность и произведение двух любых своих чисел, т.е.
![]()
Примеры.
K = {0} – нулевое (тривиальное ) кольцо является минимальным;
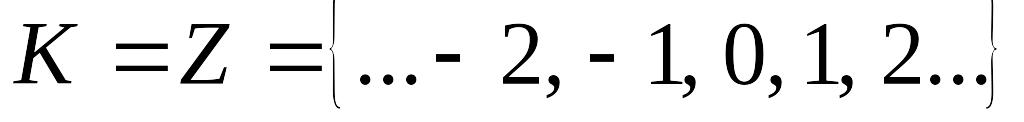 –
множество всех целых чисел;
–
множество всех целых чисел; –
множество всех рациональных чисел,
т.е. это либо целая, либо конечная, либо
периодическая бесконечная десятичная
дробь;
–
множество всех рациональных чисел,
т.е. это либо целая, либо конечная, либо
периодическая бесконечная десятичная
дробь;K = R – множество всех действительных чисел, которое состоит из рациональных и иррациональных чисел;
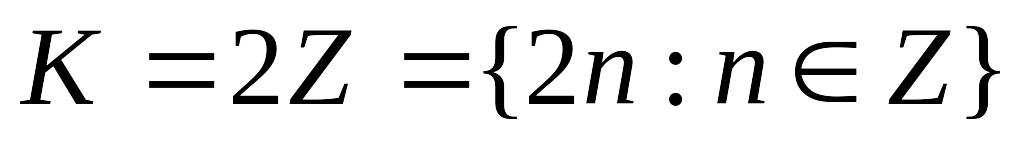 ;
;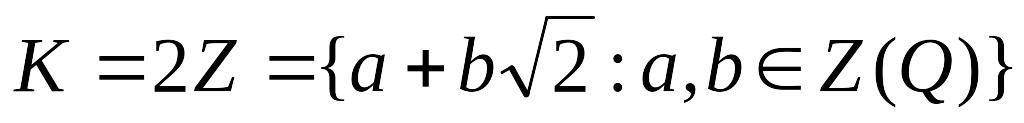 .
.
Свойства числовых колец.
Любое числовое кольцо содержит 0.
Действительно,
если
![]() ,
то в силу определения числового кольца
,
то в силу определения числового кольца
![]()
Если
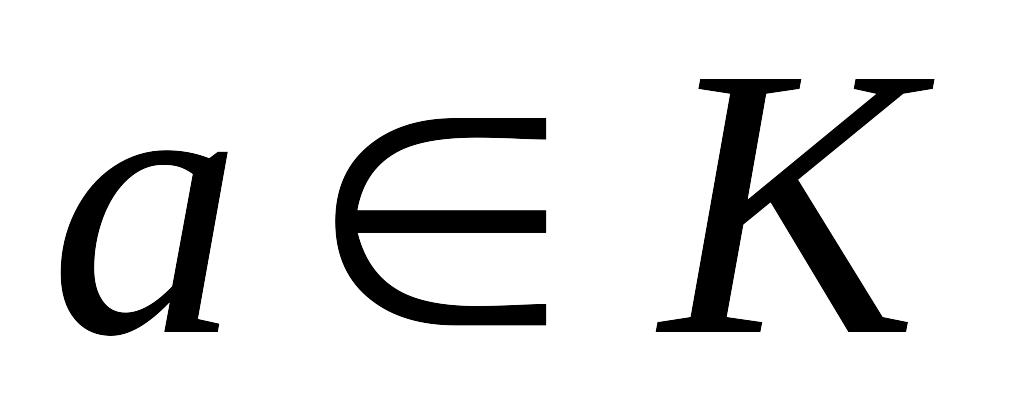 ,
то
,
то
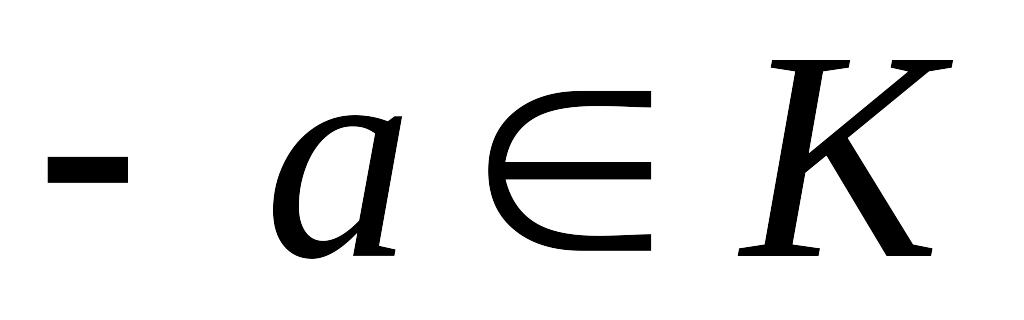 .
.
В
самом деле, если
![]() ,
то и
,
то и
![]()
Если
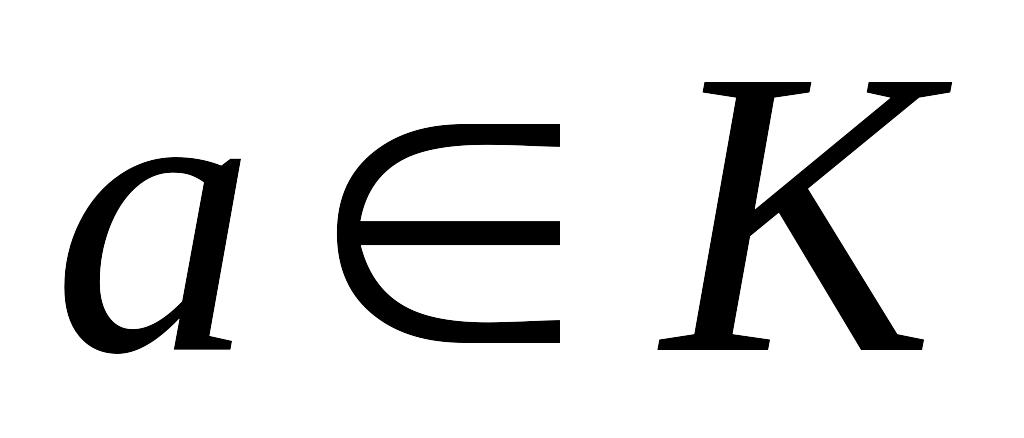 ,
то
,
то
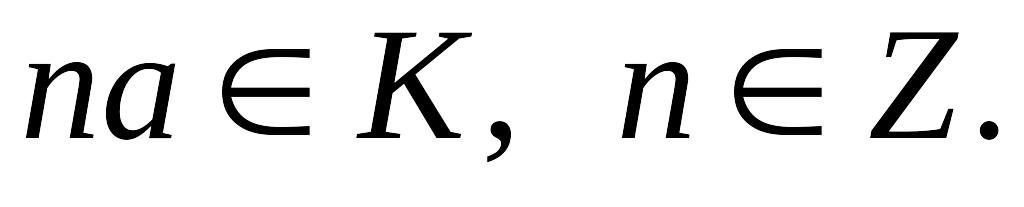
Действительно,
пусть
![]() .
Тогда
.
Тогда
![]()
Пусть![]() .
Тогда
.
Тогда
![]() .
Пусть
.
Пусть![]() .
Тогда
.
Тогда
![]() .
.
Определение. Ненулевое числовое кольцо K называется числовым полем, если оно содержит частные двух любых своих чисел (предполагается, что делитель отличен от нуля), т.е.
![]() .
.
Замечание. Всякое числовое поле является числовым кольцом.
Примеры.
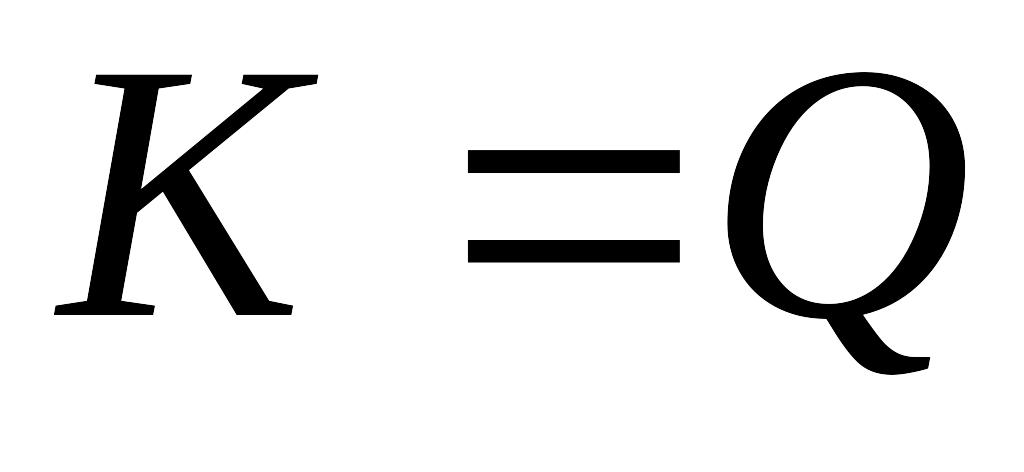 –
множество всех рациональных чисел;
–
множество всех рациональных чисел;K = R – множество всех действительных чисел;
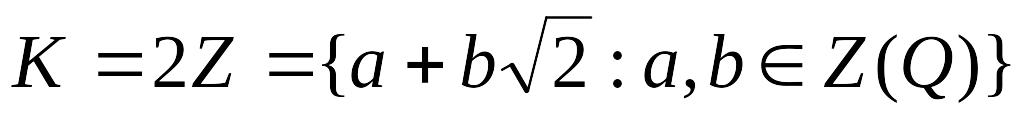 .
.
Теорема. Поле рациональных чисел Q содержится в любом числовом поле K.
Доказательство.
Пусть
K
– любое числовое поле. Возьмем
![]() .
В силу определения числового поля
.
В силу определения числового поля
![]() ,
т.е.
,
т.е.
![]() .
Так как поле K
является также и числовым кольцом, то
по третьему свойству числовых колец
(если
,
то
.
Так как поле K
является также и числовым кольцом, то
по третьему свойству числовых колец
(если
,
то
![]() )
любое целочисленное кратное единице
также принадлежит K,
т.е., если
)
любое целочисленное кратное единице
также принадлежит K,
т.е., если
![]() ,
то
,
то
![]() и поэтому
и поэтому
![]() .
.
Рассмотрим
теперь некоторые целые числа
![]() ,
причем
,
причем
![]() и воспользуемся определением поля:
и воспользуемся определением поля:
![]() .
■
.
■
