3.17. Типовой расчет

1. Даны векторы:

, , , , где

n – номер студента в групповом журнале, а k-номер группы студента.

1. Выяснить линейную зависимость системы векторов.

2. Вычислить компоненты векторов:

1. ;

2. .

2. Показать, что система векторов , , (n – номер студента в групповом журнале, а k-номер группы студента) линейно зависима. Найти ранг системы векторов.

3. Разложить вектор по системе векторов

, ,

(n – номер студента в групповом журнале, а k-номер группы студента). Сделать проверку.

3.18. Вопросы для самопроверки

1. Сформулировать определение геометрического вектора.

2. Что называется длиной вектора?

3. Сформулировать определение коллинеарных и компланарными векторов, равных и противоположных векторов?

4. Перечислите линейные операции над векторами и их свойства.

5. Определить скалярное произведение векторов и перечислить свойства скалярного произведения.

6. Что такое n-мерный вектор?

7. Перечислить операции над n-мерными векторами.

8. Какие векторы называются линейно зависимыми?

9. Сформулировать определение размерности и базиса системы векторов.

10. Дайте определение линейного векторного пространства.

11. Сформулировать определение размерности и базиса векторного пространства.

12. Как разложить произвольный вектор линейного пространства по базису?

13. Как перейти от одного базиса векторного пространства к другому?

14. Какое векторное пространство называется евклидовым?

15. Какое векторное пространство называется унитарным?

16. Что такое норма вектора?

17. Как нормировать ненулевой вектор?

18. Какой базис называется ортонормированным?

19. Сформулировать критерий ортогональности.

20. В чем суть метода ортогонализации?

3.19. Вопросы для теоретического опроса

1. Понятие вектора. Операции над векторами.

2. N-мерные векторы и действия над ними. Свойства арифметических операций над векторами.

3. Линейная зависимость векторов. Свойства линейной зависимости.

4. Базис и ранг системы векторов. Свойства базисов и рангов.

5. Переход от одного базиса к другому. Метод замещения.

6. Скалярное произведение двух векторов и его свойства. Выражение скалярного произведения через координаты перемножаемых векторов.

7. Линейно зависимые и линейно независимые системы векторов.

8. Базис и ранг системы векторов. Теорема о ранге базиса.

9. Евклидовы и унитарные пространства. Выражение скалярного произведения в координатах.

10. Норма вектора. Нормирование ненулевого вектора.

11. Ортонормированные системы векторов.

4. Матрицы

4.1. Основные понятия

Определение. Матрицей размера m´n называется система (m×n) чисел, расположенных в прямоугольной таблице, содержащей m строк и n столбцов. Матрица обозначается прописной латинской буквой и имеет вид:

,

где числа (для ), составляющие матрицу, называются элементами матрицы А, где i – номер строки, j – номер столбца, на пересечении которых находится элемент , а числа i и j – называются индексами элемента.

Столбцы матрицы можно рассматривать как векторы пространства K^m, т.е. все столбцы – это n векторов пространства K^m. Обозначим их через . Тогда матрицу можно рассматривать как систему столбцов

Аналогично, все строки матрицы – это m векторов пространства Kⁿ. Обозначим их через . Тогда матрицу можно рассматривать как систему строк

Определение. Две матрицы одинаковой размерности (m´n) называются равными, если равны их соответствующие элементы:

.

Определение. Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается:

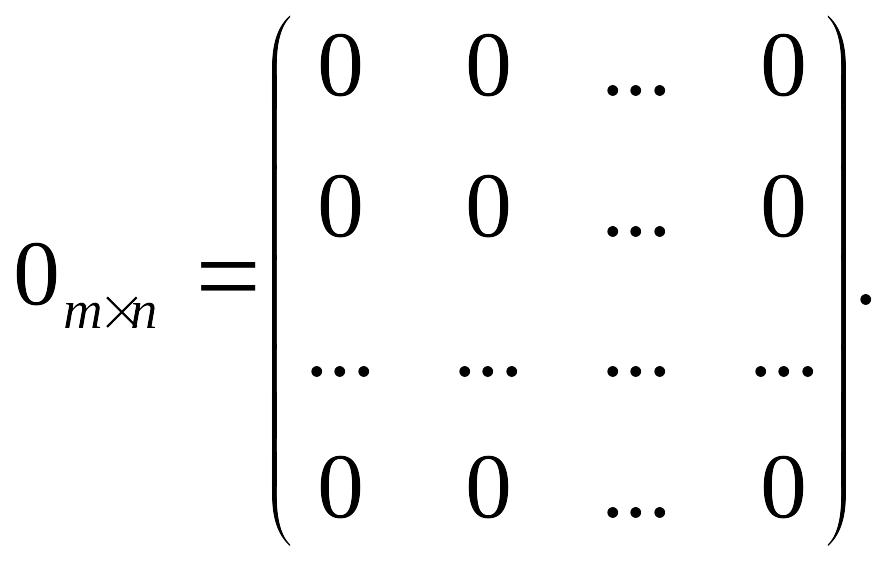
Определение. Матрица называется квадратной n – го порядка, если число ее строк равно числу ее столбцов и равно n:

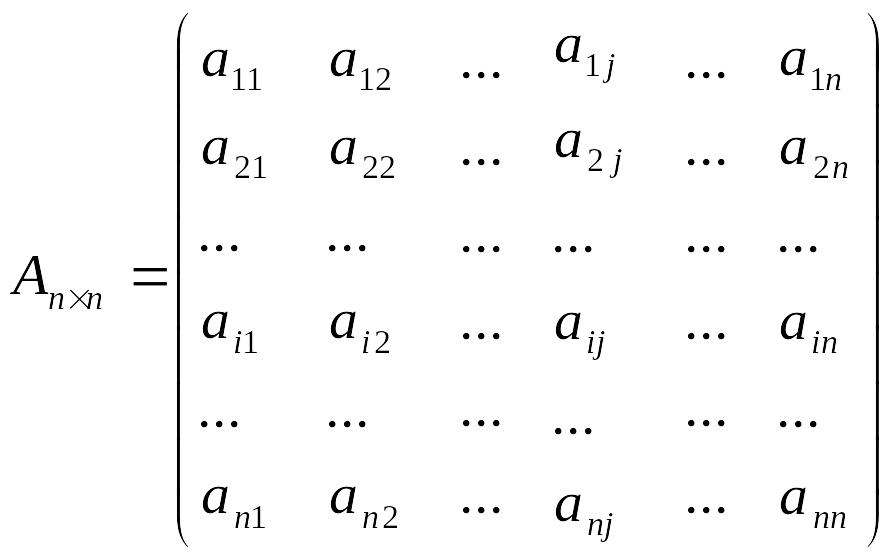
Определение. Элементы матрицы А, у которых номер строки равен номеру столбца (i=j), называются диагональными. Эти элементы лежат на отрезке, соединяющем левый верхний угол матрицы с правым нижним, и образуют главную диагональ матрицы: а₁₁, а₂₂,…, a_nn. Элементы, лежащие на отрезке, соединяющем ее левый нижним угол с правым верхний, образуют побочную диагональ: а_1n, а_2n-1,…, a_n1.

Определение. Квадратная матрица, у которой все элементы, находящиеся выше или ниже главной диагонали, равны нулю, называется треугольной матрицей, т.е. матрицы вида:

,

являются треугольными: матрица А называется треугольной сверху, а матрица В называется треугольной снизу.

Определение. Квадратная матрица, у которой все недиагональные элементы равны нулю, т.е. , называется диагональной матрицей и обозначается:

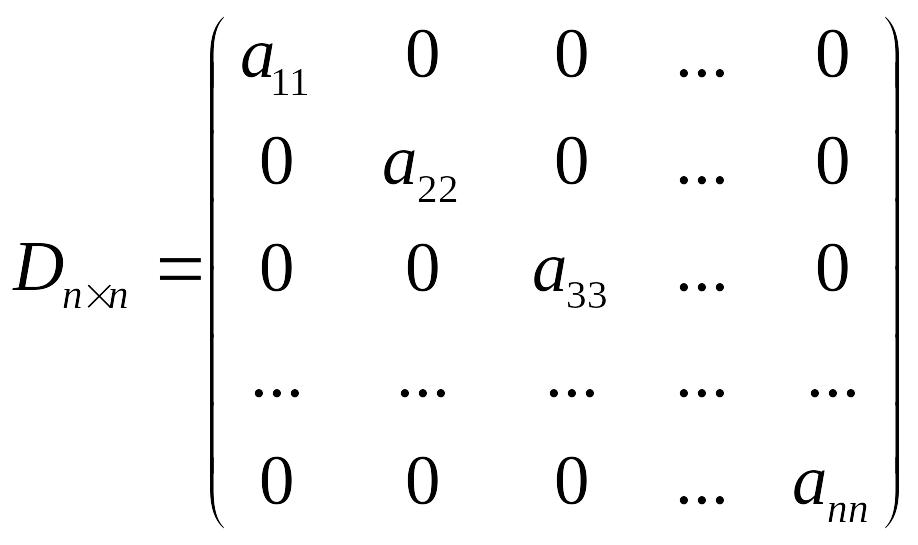
Определение. Диагональная матрица, все диагональные элементы которой равны единице, называется единичной матрицей и обозначается:

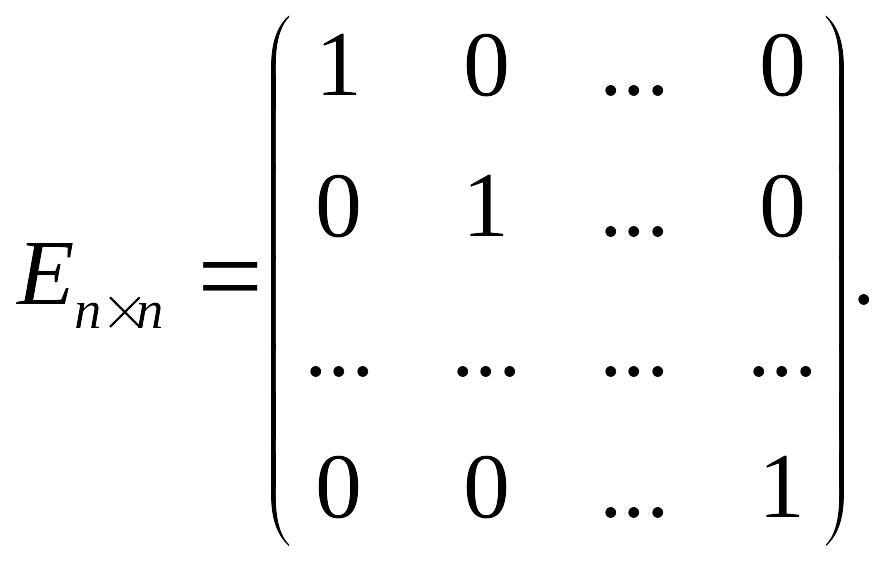
Введем в обозначение символ Кронекера . Тогда единичная матрица может быть записана в виде: .

Определение. Следом квадратной матрицы A называется сумма ее диагональных элементов: .