
- •Математика Линейная алгебра
- •Рецензенты:
- •3.6. Операции над векторами 42
- •5.6. Упражнения 91
- •Предисловие
- •1. Числовые кольца и поля. Комплексные числа
- •1.1. Основные понятия
- •1.2. Поле комплексных чисел
- •1.3. Модуль и аргумент комплексного числа. Геометрическое изображение комплексных чисел
- •1.4. Различные формы записи комплексного числа
- •1.5. Действия над комплексными числами в алгебраической форме
- •1.6. Действия над комплексными числами в тригонометрической форме
- •1.7. Действия над комплексными числами в показательной форме
- •1.8. Упражнения
- •1.9. Контрольные задания
- •1.10. Типовой расчет
- •1.11. Вопросы для самопроверки
- •1.12. Вопросы для теоретического опроса
- •2. Многочлены
- •2.1. Действия над многочленами
- •1. Сложение многочленов.
- •2. Умножение многочленов.
- •3. Деление многочленов без остатка.
- •4. Деление многочленов с остатком.
- •2.2. Схема Горнера
- •2.3. Корни многочлена
- •2.3.1. Разложение многочлена степени n на множители
- •2.3.2. Вычисление корней многочленов второй и третьей степени
- •1. Уравнения второй степени (квадратные)
- •2.4. Упражнения
- •2.5. Контрольные задания
- •2.6. Вопросы для самопроверки
- •2.7. Вопросы для теоретического опроса
- •Действия над многочленами.
- •Вычисление корней многочленов второй и третьей степени.
- •3. Линейные (векторные) пространства
- •3.1. Понятие вектора
- •3.2. Операции над векторами
- •1. Операция сложения векторов.
- •2. Операция вычитания векторов.
- •3. Умножение вектора на число.
- •4. Деление коллинеарных векторов.
- •Свойства деления:
- •3.3. Разложение вектора по ортам координатных осей
- •3.4. Скалярное произведение векторов.
- •Выражение скалярного произведения в произвольных и ортонормированных координатах.
- •3.6. Операции над векторами
- •3.7. Линейная зависимость векторов.
- •3.8. Базис и ранг системы векторов
- •3.9. Переход от одного базиса к другому. Метод замещения
- •3.10. Линейные пространства
- •3.11. Евклидовы и унитарные пространства
- •3.12. Норма вектора
- •3.13. Нормирование ненулевого вектора
- •3.14. Ортонормированные системы векторов
- •3.15. Упражнения
- •3.16. Контрольные задания
- •3.17. Типовой расчет
- •3.18. Вопросы для самопроверки
- •3.19. Вопросы для теоретического опроса
- •Переход от одного базиса к другому. Метод замещения.
- •Ортонормированные системы векторов.
- •4. Матрицы
- •4.1. Основные понятия
- •4.2 Операции над матрицами
- •Сложение матриц.
- •Умножение матрицы на число.
- •Разность матриц.
- •Умножение матриц.
- •Возведение в степень матриц.
- •Транспонирование матриц.
- •4.3. Применение элементов линейной алгебры в экономике.
- •4.4. Упражнения
- •4.5. Контрольные задания
- •Найти значение матричного многочлена , если задана матрица a.
- •4.6. Типовой расчет
- •4.7. Вопросы для самопроверки
- •4.8. Вопросы для теоретического опроса
- •5. Определители квадратных матриц
- •5.1. Перестановки
- •5.2. Определители (детерминанты) квадратных матриц
- •5.3. Свойства определителей
- •5.4. Теорема Лапласа (вычисление определителя n-ого порядка).
- •5.5. Основные методы вычисления определителя n–го порядка
- •Приведение определителя к треугольному виду.
- •5.6. Упражнения
- •5.7. Контрольные задания
- •5.8. Типовой расчет
- •5.9. Вопросы для самопроверки
- •5.10. Вопросы для теоретического опроса
- •6. Ранг матрицы
- •6.1. Основные понятия
- •6.2. Методы нахождения ранга матрицы.
- •1. Метод окаймляющих миноров
- •2. Метод элементарных преобразований
- •6.3. Упражнения
- •6.4. Контрольные задания
- •6.5. Типовой расчет
- •6.6. Вопросы для самопроверки
- •6.7. Вопросы для теоретического опроса
- •7. Обратная матрица
- •7.1. Основные понятия
- •7.2. Методы нахождения обратной матрицы
- •7.2.1. Нахождение обратной матрицы с помощью присоединенной матрицы.
- •7.2.2. Нахождение обратной матрицы методом замещения
- •7.3. Упражнения
- •7.4. Контрольные задания
- •7.5. Типовой расчет
- •7.6. Вопросы для самопроверки
- •7.7. Вопросы для теоретического опроса
- •Нахождение обратной матрицы с помощью присоединенной матрицы.
- •Нахождение обратной матрицы методом замещения.
- •8. Системы линейных уравнений (слу)
- •8.1. Неоднородные системы уравнений
- •8.2. Исследование систем линейных уравнений
- •8.3. Решение системы линейных уравнений в общем случае
- •Правило нахождения решения слу в общем случае
- •8.4. Решение систем n линейных уравнений c n неизвестными
- •8.4.1. Решение систем n линейных уравнений c n неизвестными методом Крамера
- •8.4.2. Решение систем n линейных уравнений c n неизвестными методом обратной матрицы
- •8.5. Решение систем m линейных уравнений c n неизвестными
- •8.5.1. Решение систем линейных уравнений методом Гаусса (метод последовательного исключения неизвестных)
- •8.5.2. Решение систем линейных уравнений методом замещения
- •8.6. Системы линейных однородных уравнений (ослу)
- •Правило нахождения фср ослу
- •8.7. Структура общего решения неоднородной линейной системы
- •8.8. Использование систем линейных уравнений в экономике
- •8.8.1. Прогноз выпуска продукции по запасам сырья
- •8.8.2. Модель Леонтьева многоотраслевой экономики (балансовый анализ) Балансовые соотношения
- •Линейная модель межотраслевой экономики
- •Продуктивные модели Леонтьева
- •8.9. Упражнения
- •8.10. Контрольные задания
- •8.11. Типовой расчет
- •8.12. Вопросы для самопроверки
- •8.13. Вопросы для теоретического опроса
- •9. Линейные операторы (линейные преобразования)
- •9.1. Линейный оператор и его матрица
- •9.2. Линейное преобразование в координатах
- •9.3. Зависимость между матрицами одного и того же преобразования в различных базисах. Подобные матрицы
- •9.4. Действия над линейными операторами
- •9.5. Оператор, сопряженный данному
- •9.6. Собственные значения и собственные векторы линейного оператора (матрицы)
- •9.7. Приведение матрицы линейного преобразования к диагональному виду
- •9.8. Упражнения
- •9.9. Контрольные задания
- •9.10. Типовой расчет
- •9.11. Вопросы для самопроверки
- •9.12. Вопросы для теоретического опроса
- •10. Билинейные и квадратичные формы
- •10.1 Ортогональные и симметрические матрицы
- •10.2. Билинейная и квадратичная формы
- •10.3. Квадратичные формы
- •10.4. Преобразование квадратичной формы при линейном преобразовании переменных
- •10.5. Приведение квадратичной формы к каноническому виду
- •10.6. Закон инерции квадратичных форм
- •10.7. Знакоопределенные квадратичные формы
- •10.8. Упражнения
- •10.9. Контрольные задания
- •10.5. Вопросы для самопроверки
- •10.6. Вопросы для теоретического опроса
- •11. Численные методы линейной алгебры
- •11.1. Метод Гаусса
- •11.2. Уточнение решения методом итераций
- •11.3. Метод прогонки
- •11.4. Итерационные методы решения слау
- •11.4.1. Метод простой итерации
- •11.4.2. Метод Зейделя
- •11.5. Упражнения
- •11.6. Контрольные задания
- •11.7. Типовой расчет
- •11.8. Вопросы для самопроверки
- •11.9. Вопросы для теоретического опроса
3.6. Операции над векторами
1. Сложение векторов. Под
суммой двух векторов
![]() и
и
![]() понимается вектор
понимается вектор
![]() ,
компоненты которого равны суммам
соответствующих компонент слагаемых
векторов:
,
компоненты которого равны суммам
соответствующих компонент слагаемых
векторов:
![]() .
.
2. Произведение вектора на число.
Произведением скаляра l
на вектор
называется вектор
![]() ,
координаты которого равны координатам
вектора
,
координаты которого равны координатам
вектора
![]() ,
умноженным на скаляр l:
,
умноженным на скаляр l:
![]() .
.
Определение.
Вектор
![]() ,
координаты которого являются
противоположными числами для координат
вектора
,
называется
вектором противоположным
вектору
.
,
координаты которого являются
противоположными числами для координат
вектора
,
называется
вектором противоположным
вектору
.
Определение. Вектор
![]() ,
удовлетворяющий уравнению
,
удовлетворяющий уравнению
![]() ,
называется разностью векторов
и
,
,
называется разностью векторов
и
,
![]() .
.
Вектор х, удовлетворяющий
уравнению
,
может быть найден в виде
![]() .
.
Определение. Множество K n всех n-мерных векторов над полем K, рассматриваемое вместе с определенными на нем операциями сложения векторов и умножения векторов на число, называется n-мерных линейным (векторным) пространством (K n, + , ´).
Свойства арифметических операций над векторами:
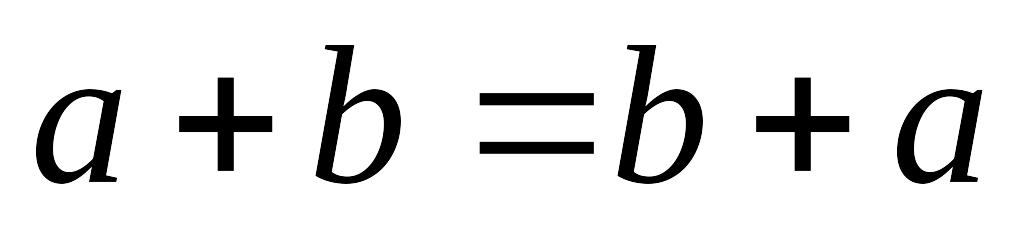 – коммутативность сложения векторов;
– коммутативность сложения векторов;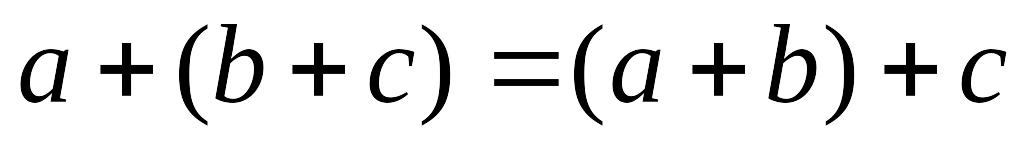 – ассоциативность сложения векторов;
– ассоциативность сложения векторов;
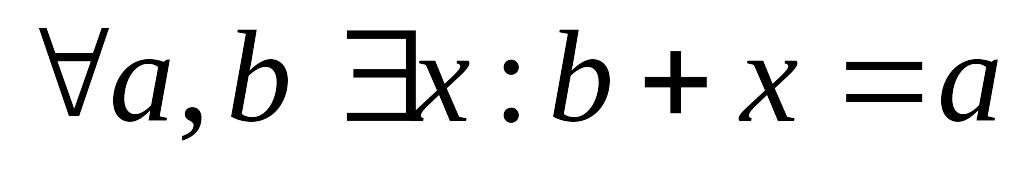 – обратимость сложения векторов;
– обратимость сложения векторов;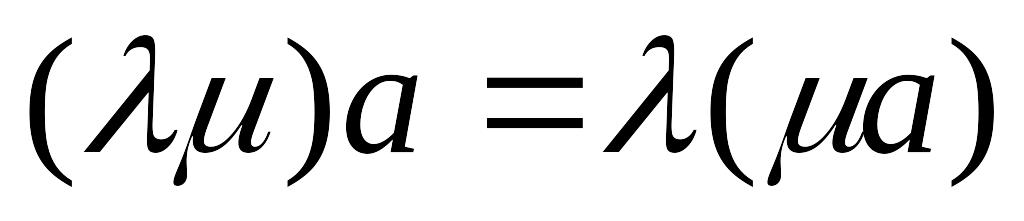 – ассоциативность умножения относительно
числового множителя)
– ассоциативность умножения относительно
числового множителя)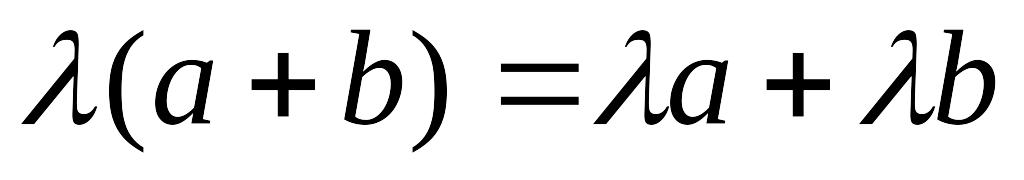 – дистрибутивность умножения относительно
сложения векторов;
– дистрибутивность умножения относительно
сложения векторов;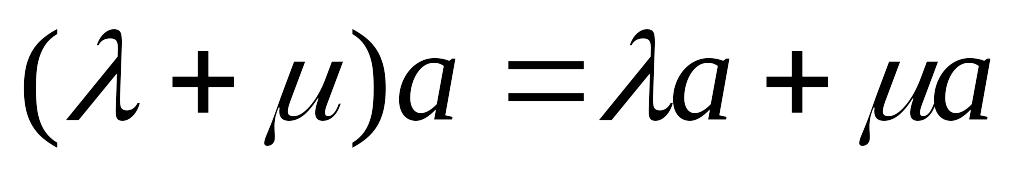 – дистрибутивность умножения относительно
числового множителя.
– дистрибутивность умножения относительно
числового множителя.
Доказательство. Докажем свойство коммутативности векторов.
![]()
Докажем свойство обратимость сложения
векторов. Найдем вектор
![]() ,
такой, что выполняется равенство
,
такой, что выполняется равенство
![]() .
.
![]()
![]() .
.
Таким образом,
![]() выполняется
выполняется
![]() или
или
![]() выполняется
выполняется
![]() и вектор
определен своими координатами
и вектор
определен своими координатами
![]() .
■
.
■
Остальные свойства доказываются аналогично.
3.7. Линейная зависимость векторов.
Определение. Вектор
называется линейной комбинацией
системы векторов
![]() ,
если существуют такие скаляры
,
если существуют такие скаляры
![]() ,
что имеет место равенство:
,
что имеет место равенство:
![]() .
.
Определение. Система векторов
![]() называется линейно зависимой,
если хотя бы один из векторов этой
системы является линейной комбинацией
других векторов системы.
называется линейно зависимой,
если хотя бы один из векторов этой
системы является линейной комбинацией
других векторов системы.
Определение. Система векторов называется линейно зависимой, если существуют такие скаляры , среди которых есть по крайней мере один, отличный от нуля, что имеет место равенство:
![]() .
.
Замечание. Для линейно зависимой
системы векторов существует неотрицательная
линейная комбинация, обращающаяся в
ноль. В случае одного вектора
![]() линейная зависимость означает, что
линейная зависимость означает, что
![]() ,
а линейная независимость –
,
а линейная независимость –
![]() .
.
Пример. Даны два вектора:
![]() ,
,
![]() .
Очевидно, что
.
Очевидно, что
![]() ,
т.е. вектор
,
т.е. вектор
![]() является линейной комбинацией вектора
является линейной комбинацией вектора
![]() .
Следовательно, вектора
и
линейно зависимы.
.
Следовательно, вектора
и
линейно зависимы.
Определение. Система векторов называется линейно независимой, если равенство
.
справедливо только в случае, когда
![]() .
.
Теорема
(Критерий линейной независимости).
Система векторов
,
где
![]() ,
является линейно зависимой тогда и
только тогда, когда хотя бы один вектор
этой системы линейно выражается через
остальные векторы.
,
является линейно зависимой тогда и
только тогда, когда хотя бы один вектор
этой системы линейно выражается через
остальные векторы.
Доказательство.
Необходимость.
Пусть векторы
линейно зависимы. По определению это
означает, что существует набор чисел
,
не все равные нулю, такие, что
![]() .
Предположим, что
.
Предположим, что
![]() .
Тогда
.
Тогда
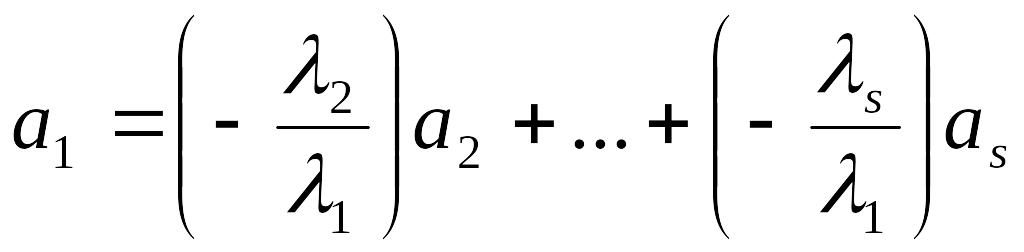
т.е.
вектор
![]() линейно выражается через остальные
линейно выражается через остальные
![]() .
.
Достаточность. Пусть вектор линейно выражается через остальные :
![]()
а, значит, неотрицательная линейная комбинация векторов обращается в ноль. Тогда система векторов линейно зависима. n
Свойства линейной зависимости
Если какая-либо подсистема векторов
 линейно зависима,
то линейно зависима и вся система
векторов
.
линейно зависима,
то линейно зависима и вся система
векторов
.
Доказательство. Пусть подсистема
векторов
(r < s)
линейно зависима. По определению это
означает, что существуют числа
![]() ,
не все одновременно равные нулю, такие,
что
,
не все одновременно равные нулю, такие,
что
![]() .
Не нарушая равенства, добавим в левую
часть остальные (s -
r) векторов с нулевыми
.
Не нарушая равенства, добавим в левую
часть остальные (s -
r) векторов с нулевыми
![]() :
:
![]()
Получаем, что линейная комбинация векторов равна нулю, что по определению означает линейную зависимость системы векторов .n
Если система векторов линейно независима, то и любая ее подсистема будет линейно независимой.
Доказательство. Предположим, что в линейно независимой системе существует линейно зависимая подсистема. Тогда по свойству 1 вся система векторов должна быть линейно зависимой, что противоречит условию. n
Если система векторов линейно независима, а система
 линейно зависима,
то вектор b
линейно выражается через
.
линейно зависима,
то вектор b
линейно выражается через
.
Доказательство. По условию система
линейно зависима, следовательно,
существует набор чисел
![]() ,
не все равные нулю, такие что
,
не все равные нулю, такие что
![]()
Покажем, что
![]() .
Предположим, что
.
Предположим, что
![]() ,
тогда
,
тогда
![]() ,
причем не все
,
причем не все
![]() равны нулю. Это означает линейную
зависимость системы
,
что противоречит условию. Поэтому
и
равны нулю. Это означает линейную
зависимость системы
,
что противоречит условию. Поэтому
и
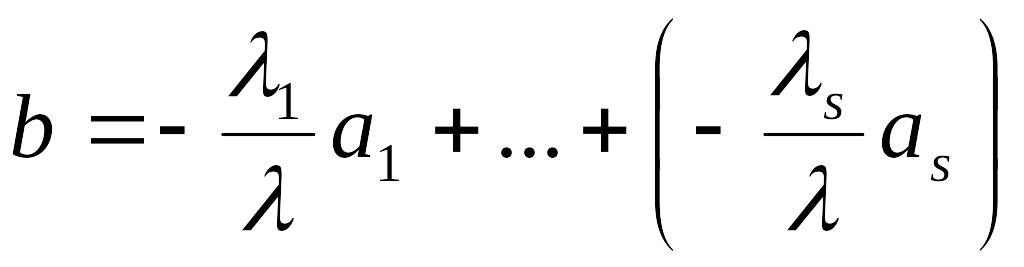 .n
.n
Два вектора линейно зависимы тогда и только тогда, когда они пропорциональны.
Доказательство.
Необходимость.
Пусть векторы
и
![]() линейно зависимы,
т.е. существуют числа
линейно зависимы,
т.е. существуют числа
![]() и
и
![]() ,
одновременно не равные нулю, такие, что
,
одновременно не равные нулю, такие, что
![]() .
Предположим, что
.
Тогда
.
Предположим, что
.
Тогда
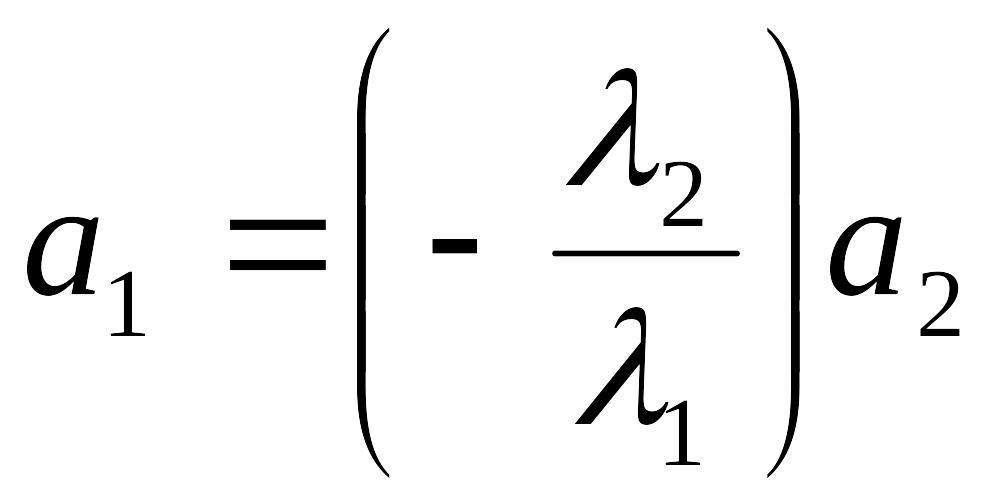 ,
следовательно
и
пропорциональны.
,
следовательно
и
пропорциональны.
Достаточность.
Пусть векторы
и
пропорциональны, т.е.
![]() (или
(или
![]() ).
Тогда
).
Тогда
![]() - это линейная комбинация векторов
и
,
поэтому
и
линейно зависимы. n
- это линейная комбинация векторов
и
,
поэтому
и
линейно зависимы. n
Если система векторов содержит хотя бы два пропорциональных вектора или нулевой вектор, то она линейно зависима.
Доказательство следует из свойства 4.
Теорема. Пусть даны две системы векторов
![]() (I)
(I)
![]() (II)
(II)
причем,
(I)
линейно независима и каждый вектор этой
системы линейно выражается через векторы
системы (II).
Тогда
![]() .
.
Доказательство.
Докажем методом математической индукции
по количеству векторов системы (II).
Установим справедливость теоремы для
q=1.
Докажем, что
![]() .
Предположим обратное, что
.
Предположим обратное, что
![]() .
Это означает, что в системе (I)
имеются по крайней мере два вектора,
которые линейно выражаются через
.
Это означает, что в системе (I)
имеются по крайней мере два вектора,
которые линейно выражаются через
![]() :
:
![]()
![]() .
.
Ясно, что
![]() (если
(если
![]() ,
то
,
то
![]() и система (I) была бы
линейно зависимой).
и система (I) была бы
линейно зависимой).
Таким образом,
![]() ,
т.е. векторы
и
пропорциональны, поэтому по свойству
4 система (I) линейно
зависима. Получили противоречие условию,
следовательно, наше предположение не
верно и
,
т.е. векторы
и
пропорциональны, поэтому по свойству
4 система (I) линейно
зависима. Получили противоречие условию,
следовательно, наше предположение не
верно и
![]() .
.
Пусть утверждение теоремы верно в
случае, когда система (II)
содержит
![]() вектор. Установим справедливость теоремы
для случая q векторов.
По условию все векторы системы (I)
линейно выражаются через векторы (II).
вектор. Установим справедливость теоремы
для случая q векторов.
По условию все векторы системы (I)
линейно выражаются через векторы (II).
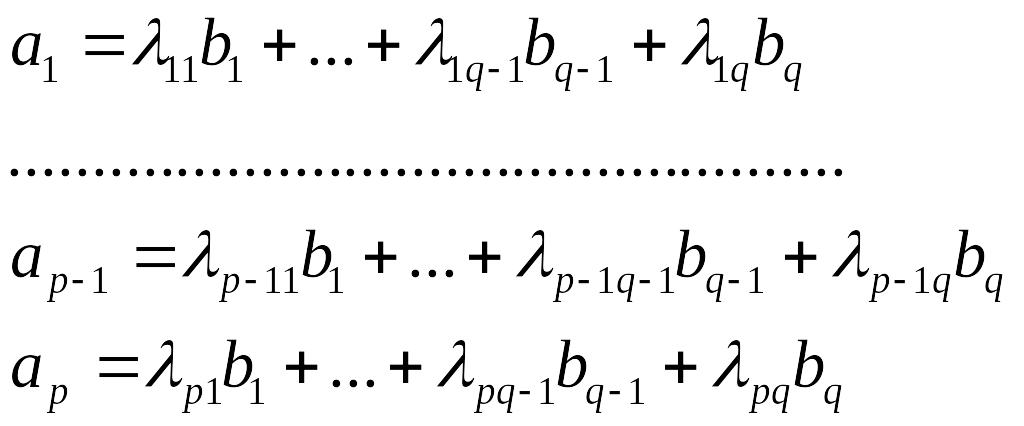 (1)
(1)
Рассмотрим два возможных случая.
1) В равенствах (1) все скаляры при
![]() равны нулю, т.е.
равны нулю, т.е.
![]() .
Тогда равенства указывают на то, что
система (I) линейно
выражается через векторы
.
Тогда равенства указывают на то, что
система (I) линейно
выражается через векторы
![]() и по предположению индукции
и по предположению индукции
![]() .
.
2) Не все скаляры в равенствах (1) при
![]() равны нулю. Пусть
равны нулю. Пусть
![]() .
В первых (p-1) равенствах
из (1) исключим
с помощью последнего соотношения. Для
этого последнее равенство умножим на
.
В первых (p-1) равенствах
из (1) исключим
с помощью последнего соотношения. Для
этого последнее равенство умножим на
![]() вычтем его из i-го
равенства
вычтем его из i-го
равенства
![]() Тогда получим
Тогда получим
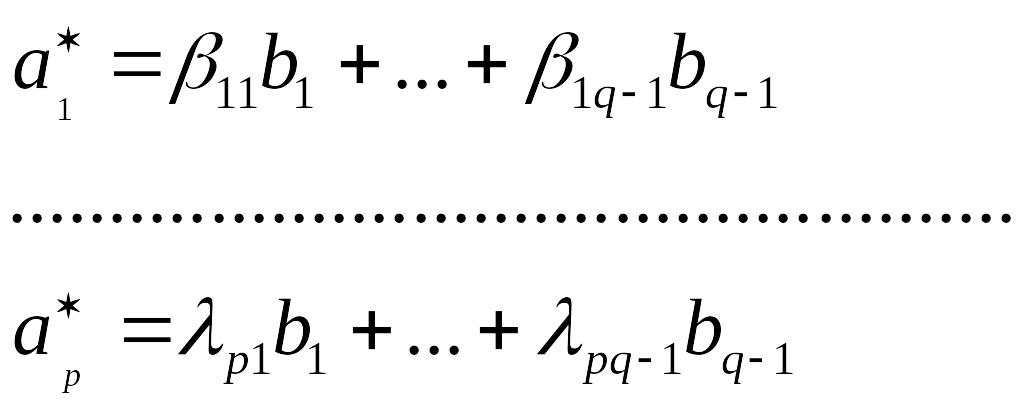 (2)
(2)
где
![]()
Получаем две системы
![]() (I*)
(I*)
![]() (II*)
(II*)
Покажем, что система (I*)
является линейно независимой. Пусть
имеются
![]() такие, что
такие, что
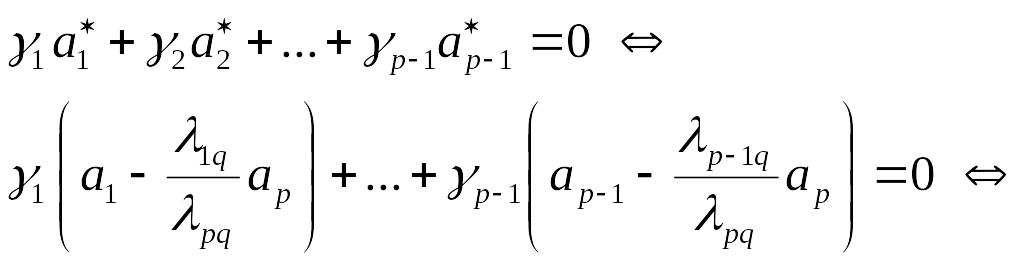
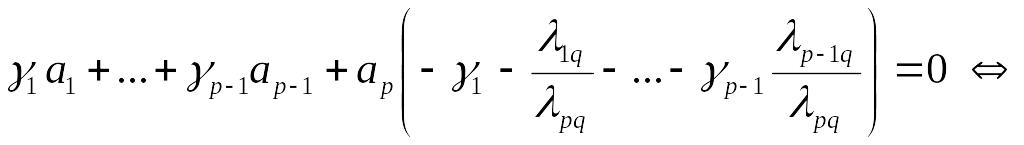
![]() (3)
(3)
где
![]() .
.
По условию теоремы система (I)
линейно независима, т.е. равенство (3)
возможно только при
![]() .
Система (I*) является
подсистемой линейно независимой системы
(I), следовательно, по
свойству 2 система (I*)
линейно независима. Равенства (2) указывают
на то, что все векторы линейно независимой
системы (I*) линейно
выражаются через систему (II
*), в которой есть q-1
вектор. По предположению индукции число
векторов в (I*) р-1
не превосходит q-1,
следовательно,
.
Система (I*) является
подсистемой линейно независимой системы
(I), следовательно, по
свойству 2 система (I*)
линейно независима. Равенства (2) указывают
на то, что все векторы линейно независимой
системы (I*) линейно
выражаются через систему (II
*), в которой есть q-1
вектор. По предположению индукции число
векторов в (I*) р-1
не превосходит q-1,
следовательно,
![]() .
■
.
■
Теорема (О максимальном числе линейно независимых векторов). В координатном линейном векторном пространстве Kn существуют линейно независимые системы, состоящие из n векторов, через которые линейно выражаются все векторы пространства Kn. Любая система, состоящая из более чем n векторов, является линейно зависимой.
Доказательство. В пространстве Kn рассмотрим единичные векторы
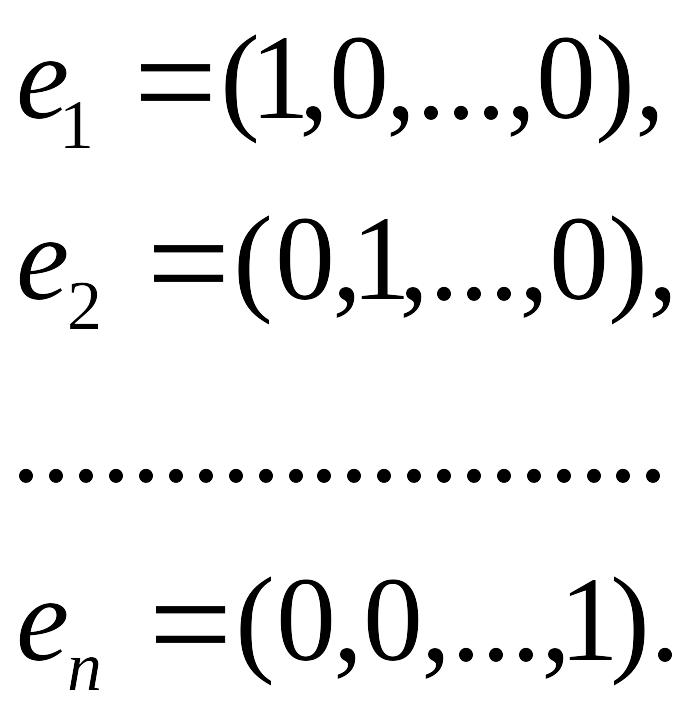
Покажем
их линейную независимость. Пусть
![]()
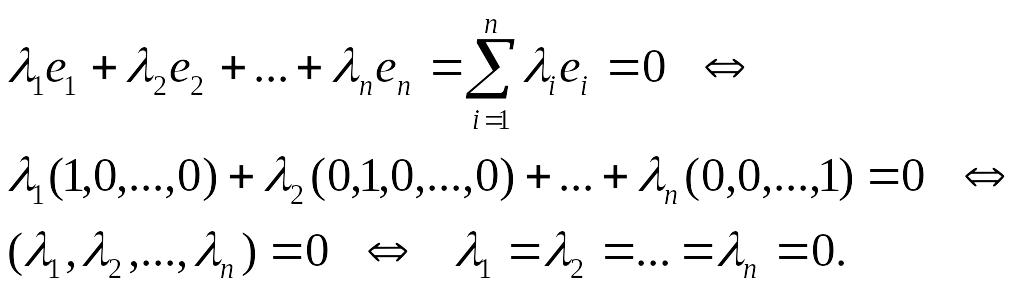
Пусть
![]() - некоторый произвольный вектор.
Представим его в виде линейной комбинации
единичных векторов
- некоторый произвольный вектор.
Представим его в виде линейной комбинации
единичных векторов
![]() :
:
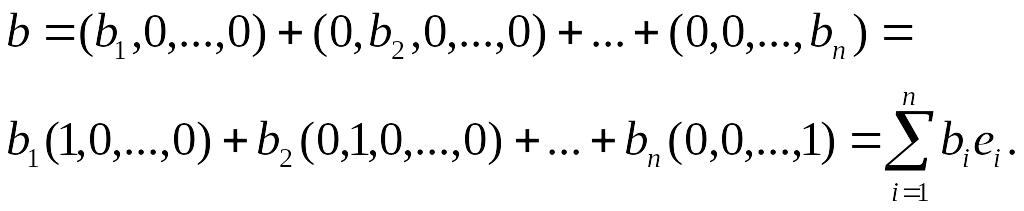
Пусть
![]() - любая линейно независимая система
векторов пространства Kn.
Все векторы
- любая линейно независимая система
векторов пространства Kn.
Все векторы
![]() линейно выражаются через единичные
векторы
линейно выражаются через единичные
векторы
![]() .
По основной теореме о линейной
независимости
.
По основной теореме о линейной
независимости
![]() ,
поэтому если система
,
поэтому если система
![]() содержит более n
векторов, то она линейно зависима. ■
содержит более n
векторов, то она линейно зависима. ■
Определение.
Линейно
независимая система векторов
![]() называется максимальной
линейно независимой подсистемой
системы векторов А
(непустое,
может быть, бесконечное множество
векторов), если при присоединении к ней
любого вектора
называется максимальной
линейно независимой подсистемой
системы векторов А
(непустое,
может быть, бесконечное множество
векторов), если при присоединении к ней
любого вектора
![]() она становится линейно зависимой.
она становится линейно зависимой.
Любая линейно независимая система, состоящая из n векторов, является максимальной в пространстве Kn.
