
- •Математика Линейная алгебра
- •Рецензенты:
- •3.6. Операции над векторами 42
- •5.6. Упражнения 91
- •Предисловие
- •1. Числовые кольца и поля. Комплексные числа
- •1.1. Основные понятия
- •1.2. Поле комплексных чисел
- •1.3. Модуль и аргумент комплексного числа. Геометрическое изображение комплексных чисел
- •1.4. Различные формы записи комплексного числа
- •1.5. Действия над комплексными числами в алгебраической форме
- •1.6. Действия над комплексными числами в тригонометрической форме
- •1.7. Действия над комплексными числами в показательной форме
- •1.8. Упражнения
- •1.9. Контрольные задания
- •1.10. Типовой расчет
- •1.11. Вопросы для самопроверки
- •1.12. Вопросы для теоретического опроса
- •2. Многочлены
- •2.1. Действия над многочленами
- •1. Сложение многочленов.
- •2. Умножение многочленов.
- •3. Деление многочленов без остатка.
- •4. Деление многочленов с остатком.
- •2.2. Схема Горнера
- •2.3. Корни многочлена
- •2.3.1. Разложение многочлена степени n на множители
- •2.3.2. Вычисление корней многочленов второй и третьей степени
- •1. Уравнения второй степени (квадратные)
- •2.4. Упражнения
- •2.5. Контрольные задания
- •2.6. Вопросы для самопроверки
- •2.7. Вопросы для теоретического опроса
- •Действия над многочленами.
- •Вычисление корней многочленов второй и третьей степени.
- •3. Линейные (векторные) пространства
- •3.1. Понятие вектора
- •3.2. Операции над векторами
- •1. Операция сложения векторов.
- •2. Операция вычитания векторов.
- •3. Умножение вектора на число.
- •4. Деление коллинеарных векторов.
- •Свойства деления:
- •3.3. Разложение вектора по ортам координатных осей
- •3.4. Скалярное произведение векторов.
- •Выражение скалярного произведения в произвольных и ортонормированных координатах.
- •3.6. Операции над векторами
- •3.7. Линейная зависимость векторов.
- •3.8. Базис и ранг системы векторов
- •3.9. Переход от одного базиса к другому. Метод замещения
- •3.10. Линейные пространства
- •3.11. Евклидовы и унитарные пространства
- •3.12. Норма вектора
- •3.13. Нормирование ненулевого вектора
- •3.14. Ортонормированные системы векторов
- •3.15. Упражнения
- •3.16. Контрольные задания
- •3.17. Типовой расчет
- •3.18. Вопросы для самопроверки
- •3.19. Вопросы для теоретического опроса
- •Переход от одного базиса к другому. Метод замещения.
- •Ортонормированные системы векторов.
- •4. Матрицы
- •4.1. Основные понятия
- •4.2 Операции над матрицами
- •Сложение матриц.
- •Умножение матрицы на число.
- •Разность матриц.
- •Умножение матриц.
- •Возведение в степень матриц.
- •Транспонирование матриц.
- •4.3. Применение элементов линейной алгебры в экономике.
- •4.4. Упражнения
- •4.5. Контрольные задания
- •Найти значение матричного многочлена , если задана матрица a.
- •4.6. Типовой расчет
- •4.7. Вопросы для самопроверки
- •4.8. Вопросы для теоретического опроса
- •5. Определители квадратных матриц
- •5.1. Перестановки
- •5.2. Определители (детерминанты) квадратных матриц
- •5.3. Свойства определителей
- •5.4. Теорема Лапласа (вычисление определителя n-ого порядка).
- •5.5. Основные методы вычисления определителя n–го порядка
- •Приведение определителя к треугольному виду.
- •5.6. Упражнения
- •5.7. Контрольные задания
- •5.8. Типовой расчет
- •5.9. Вопросы для самопроверки
- •5.10. Вопросы для теоретического опроса
- •6. Ранг матрицы
- •6.1. Основные понятия
- •6.2. Методы нахождения ранга матрицы.
- •1. Метод окаймляющих миноров
- •2. Метод элементарных преобразований
- •6.3. Упражнения
- •6.4. Контрольные задания
- •6.5. Типовой расчет
- •6.6. Вопросы для самопроверки
- •6.7. Вопросы для теоретического опроса
- •7. Обратная матрица
- •7.1. Основные понятия
- •7.2. Методы нахождения обратной матрицы
- •7.2.1. Нахождение обратной матрицы с помощью присоединенной матрицы.
- •7.2.2. Нахождение обратной матрицы методом замещения
- •7.3. Упражнения
- •7.4. Контрольные задания
- •7.5. Типовой расчет
- •7.6. Вопросы для самопроверки
- •7.7. Вопросы для теоретического опроса
- •Нахождение обратной матрицы с помощью присоединенной матрицы.
- •Нахождение обратной матрицы методом замещения.
- •8. Системы линейных уравнений (слу)
- •8.1. Неоднородные системы уравнений
- •8.2. Исследование систем линейных уравнений
- •8.3. Решение системы линейных уравнений в общем случае
- •Правило нахождения решения слу в общем случае
- •8.4. Решение систем n линейных уравнений c n неизвестными
- •8.4.1. Решение систем n линейных уравнений c n неизвестными методом Крамера
- •8.4.2. Решение систем n линейных уравнений c n неизвестными методом обратной матрицы
- •8.5. Решение систем m линейных уравнений c n неизвестными
- •8.5.1. Решение систем линейных уравнений методом Гаусса (метод последовательного исключения неизвестных)
- •8.5.2. Решение систем линейных уравнений методом замещения
- •8.6. Системы линейных однородных уравнений (ослу)
- •Правило нахождения фср ослу
- •8.7. Структура общего решения неоднородной линейной системы
- •8.8. Использование систем линейных уравнений в экономике
- •8.8.1. Прогноз выпуска продукции по запасам сырья
- •8.8.2. Модель Леонтьева многоотраслевой экономики (балансовый анализ) Балансовые соотношения
- •Линейная модель межотраслевой экономики
- •Продуктивные модели Леонтьева
- •8.9. Упражнения
- •8.10. Контрольные задания
- •8.11. Типовой расчет
- •8.12. Вопросы для самопроверки
- •8.13. Вопросы для теоретического опроса
- •9. Линейные операторы (линейные преобразования)
- •9.1. Линейный оператор и его матрица
- •9.2. Линейное преобразование в координатах
- •9.3. Зависимость между матрицами одного и того же преобразования в различных базисах. Подобные матрицы
- •9.4. Действия над линейными операторами
- •9.5. Оператор, сопряженный данному
- •9.6. Собственные значения и собственные векторы линейного оператора (матрицы)
- •9.7. Приведение матрицы линейного преобразования к диагональному виду
- •9.8. Упражнения
- •9.9. Контрольные задания
- •9.10. Типовой расчет
- •9.11. Вопросы для самопроверки
- •9.12. Вопросы для теоретического опроса
- •10. Билинейные и квадратичные формы
- •10.1 Ортогональные и симметрические матрицы
- •10.2. Билинейная и квадратичная формы
- •10.3. Квадратичные формы
- •10.4. Преобразование квадратичной формы при линейном преобразовании переменных
- •10.5. Приведение квадратичной формы к каноническому виду
- •10.6. Закон инерции квадратичных форм
- •10.7. Знакоопределенные квадратичные формы
- •10.8. Упражнения
- •10.9. Контрольные задания
- •10.5. Вопросы для самопроверки
- •10.6. Вопросы для теоретического опроса
- •11. Численные методы линейной алгебры
- •11.1. Метод Гаусса
- •11.2. Уточнение решения методом итераций
- •11.3. Метод прогонки
- •11.4. Итерационные методы решения слау
- •11.4.1. Метод простой итерации
- •11.4.2. Метод Зейделя
- •11.5. Упражнения
- •11.6. Контрольные задания
- •11.7. Типовой расчет
- •11.8. Вопросы для самопроверки
- •11.9. Вопросы для теоретического опроса
3.2. Операции над векторами
1. Операция сложения векторов.
П усть
и
- векторы на плоскости или в пространстве.
усть
и
- векторы на плоскости или в пространстве.
Определение.
Суммой
векторов
и
называют вектор
![]() ,
соединяющий
начало вектора
и конец вектора
при условии, что векторы
и
отложены последовательно.
,
соединяющий
начало вектора
и конец вектора
при условии, что векторы
и
отложены последовательно.
В общем случае суммой векторов называется вектор, определяемый правилом многоугольника или правилом параллелограмма.
Е сли
складывают только два вектора, вместо
правила многоугольника применяют
правило параллелограмма.
сли
складывают только два вектора, вместо
правила многоугольника применяют
правило параллелограмма.
Правило параллелограмма. Сумма двух неколлинеарных векторов, отложенных от общего начала, совпадает с диагональю параллелограмма, построенного на слагаемых векторах как на сторонах, и выходящей из того же начала.
П равило
многоугольника.
Чтобы найти сумму векторов
равило
многоугольника.
Чтобы найти сумму векторов
![]() нужно от произвольной точки пространства
отложить первый вектор
нужно от произвольной точки пространства
отложить первый вектор
![]() ,
затем от его конца отложить второй
вектор
,
затем от его конца отложить второй
вектор
![]() и т.д. Вектор, начало которого совпадает
с началом первого, а конец – с концом
последнего, называется суммой
данных векторов.
и т.д. Вектор, начало которого совпадает
с началом первого, а конец – с концом
последнего, называется суммой
данных векторов.
Алгебраические свойства сложения:
 -
коммутативность сложения векторов;
-
коммутативность сложения векторов; -
ассоциативность сложения векторов;
-
ассоциативность сложения векторов; ;
; .
.
2. Операция вычитания векторов.
О пределение.
Разностью
векторов
и
называется вектор
пределение.
Разностью
векторов
и
называется вектор
![]() ,
удовлетворяющий
уравнению
,
удовлетворяющий
уравнению
![]() .
Разность
векторов обозначается так:
.
Разность
векторов обозначается так:
![]() .
.
Чтобы
построить разность
![]() геометрически, необходимо отложить
векторы
и
от общего начала, концы соединить
отрезком и стрелку поставить в сторону
уменьшаемого.
геометрически, необходимо отложить
векторы
и
от общего начала, концы соединить
отрезком и стрелку поставить в сторону
уменьшаемого.
3. Умножение вектора на число.
Пусть - данный вектор; λ - скаляр.
Определение.
Произведением
числа λ на
вектор
называется вектор
![]() ,
определяемый
условиями:
,
определяемый
условиями:

Если λ > 0, то
 ,
если λ < 0, то
,
если λ < 0, то
 .
.
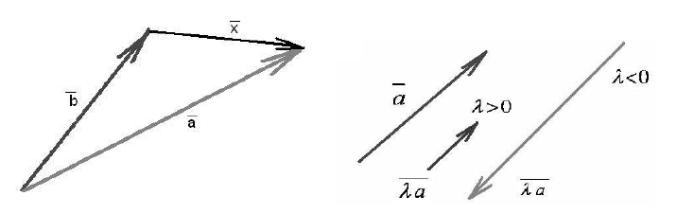
Алгебраические свойства умножения вектора на число:
 -
ассоциативность
умножения вектора на число;
-
ассоциативность
умножения вектора на число;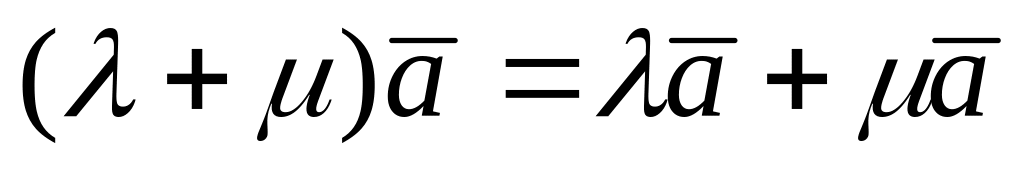 -
дистрибутивность
умножения вектора на число;
-
дистрибутивность
умножения вектора на число; -
дистрибутивность
умножения числа на вектор;
-
дистрибутивность
умножения числа на вектор;
Теорема (необходимое и достаточное условие коллинеарности векторов). Для того чтобы векторы плоскости и были коллинеарными необходимо и достаточно, чтобы они были пропорциональны:
![]() или
или
![]() .
.
4. Деление коллинеарных векторов.
Пусть имеются два коллинеарных ненулевых вектора и .
Определение.
Частным
от деления
вектора
на вектор
называют число λ,
для которого выполняется
равенство
![]() .
.
Таким
образом,
![]() .
.
Свойства деления:
Пусть , и
 - коллинеарные векторы, причем
- коллинеарные векторы, причем
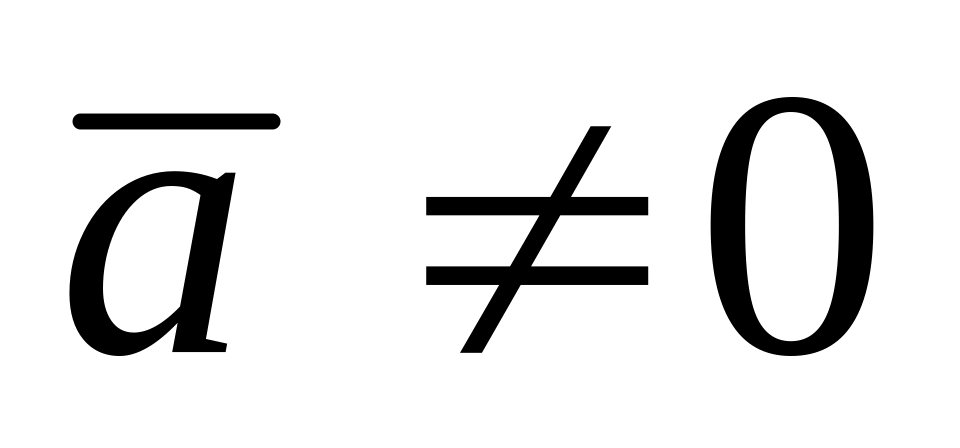 .
Тогда
.
Тогда
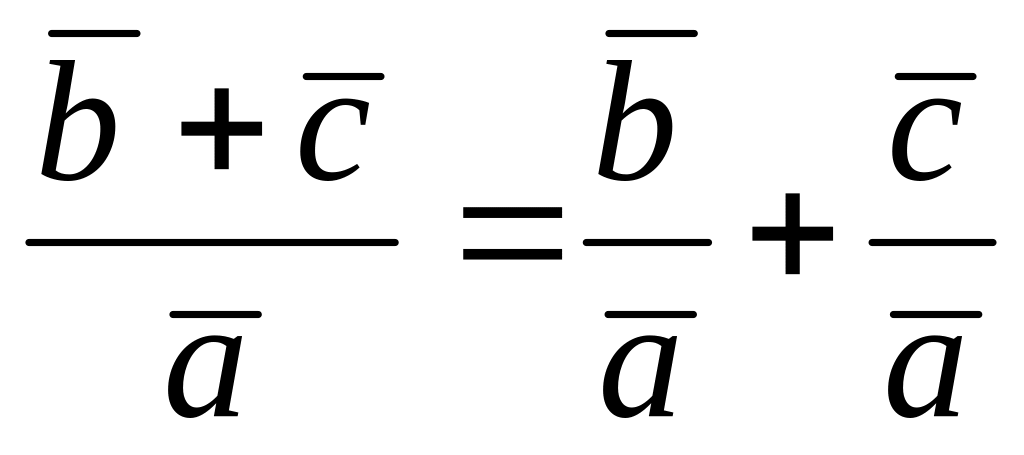 .
.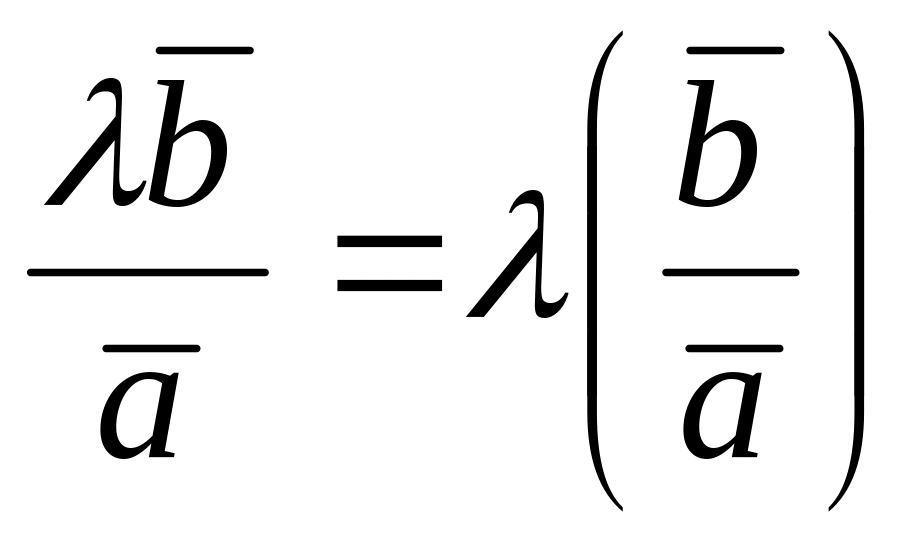 ,если
.
,если
.Неколлинеарные векторы делить нельзя.
3.3. Разложение вектора по ортам координатных осей
П

![]() можно представить и притом единственным
образом в виде линейной комбинации этих
векторов
можно представить и притом единственным
образом в виде линейной комбинации этих
векторов
![]()
Действительно,
по определению суммы двух векторов
![]() .
.
Так
как
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
то
,
то
![]() .
Обозначив
.
Обозначив
![]() ,
,
![]() и
и
![]() )
получим
)
получим
![]() .
.
Эта формула называется разложением вектора по ортам координатных осей, числа ах, ау, az называются координатами вектора .
Векторное
равенство
записывается в символическом виде
![]() .
.
З

![]() .
На основании теоремы о длине прямоугольного
параллелепипеда можно записать
.
На основании теоремы о длине прямоугольного
параллелепипеда можно записать
![]() .
.
Определение. Длиной вектора называется число, равное длине отрезка, которое определяется по формуле:
![]() .
.
Вектор образует с координатными осями Ох, Оу, Oz углы α, β и γ соответственно. По свойству проекции вектора на ось
![]()
![]()
![]() .
.
Таким образом, направление вектора определяется с помощью так называемых направляющих косинусов:
![]() ,
,
![]() ,
,
![]() .
.
Направляющие косинусы связаны между собой соотношением
![]() .
.
