Магнитное поле.

Пусть магнитное поле не меняется во времени:

В этом случае уравнения Максвелла имеют вид:

Из соотношения

Исследуем соотношения:

и зададимся вопросом, а нельзя ли для магнитного поля ввести функцию потенциала, хотя ?

У нас есть выражение:

Что это дает?

Из математики известно, что если , где - какой-то вектор, то:

, в этом случае - векторный потенциал, для этого вектора существует только одно требование, чтобы

Поскольку вектор - не изменяется, то если к вектору мы прибавим не только постоянную, но и широкий класс потенциальных функций, то:

тогда:

, так как

Возникает вопрос, а какому уравнению удовлетворяет функция (вектор)

Допустим, что магнитных сред нет или среда однородная, то:

, или:

, или:

- это векторное уравнение и достаточно громоздкое, попробуем его упростить. Для этого воспользуемся произволом выбора вектора . Пусть этот вектор удовлетворяет условию: , тогда справедливо уравнение:

- выражение для векторного потенциала (аналог уравнения Пуассона) .

Вывод: вектор удовлетворяет уравнению Пуассона и если - уравнение Лапласа.

Решение уравнения было:

По аналогии, решение уравнения , будет: - векторный потенциал.

Если нашли , т.е. надо интегрировать по объему, где есть .

Рассмотрим случай, когда проводник достаточно тонкий.

- - для тонкого линейного проводника. - - для замкнутого линейного контура - - поле найдено (закон Био-Савара)

В общем случае можно показать, что:

- закон Био-Савара в общем виде.

Возникает вопрос? Нельзя ли найти магнитный поток, если известна функция потенциала:

- поток, охватываемый контур

Чтобы воспользоваться , надо установить граничные условия.

- поток через контур , так как - тангенциальные составляющие векторного потенциала не делают скачка на границе.

Если мы выбрали, что

Рассмотрим связь между векторами: .

- это соотношение справедливо только для линейных сред.

Сила, действующая на движущейся заряд:

,

для вакуума справедлив закон полного тока:

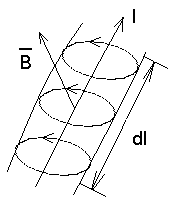
Если есть магнитная среда, то ее можно представить как эквивалентную тому, что есть молекулярные токи и эти токи ориентируются в направлении поля.

	Тогда справедливо будет записать, что: Возникает вопрос о том, как учитывать эти молекулярные токи?
	Пусть объем заключает в себя несколько контуров. - число элементарных контуров в единице объема. - число контуров в элементе объема - ток элементарного контура - сумма токов в объеме

- магнитный момент одного контура

- магнитный момент единице объема (вектор намагниченности)

Вывод:

или , тогда - закон полного тока. В этом смысл введения вектора .

Таким образом:

- плотность связанных токов, обусловлена поляризацией.

Если - это значит, что одинаково распределение токов, т.е. они друг друга компенсируют.

Рассмотрим связанные токи:

Если - среда не магнитная.

Если есть (если есть ток, то есть и поляризованный ток)

Если , то среда должна быть неоднородной, чтобы

Если параллелен вектору

- достигает максимальных значений на поверхности тел, что соответствует тому, что на поверхности будет поверхностная плотность тока.

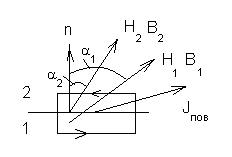
Проанализируем граничные условия.

1. Если 2. 3.

- по теореме Стокса

, следовательно:
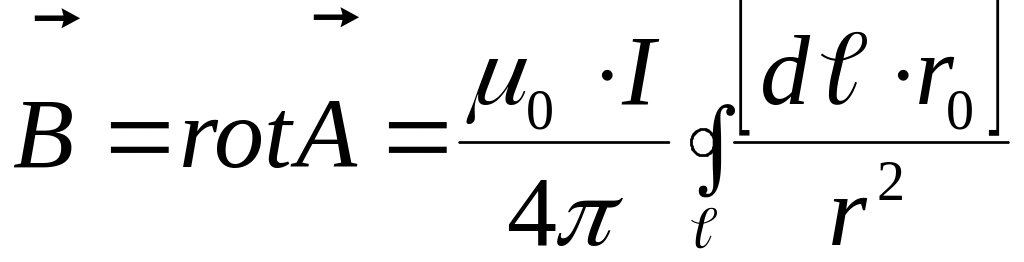