Энергия и силы в электрическом поле.

Из курса физики известно:

(1) ( по всем зарядам)

(2)

где - плотность энергии

Эти выражения для энергии электростатического поля приводят к одному и тому же результату и следуют одно из другого.

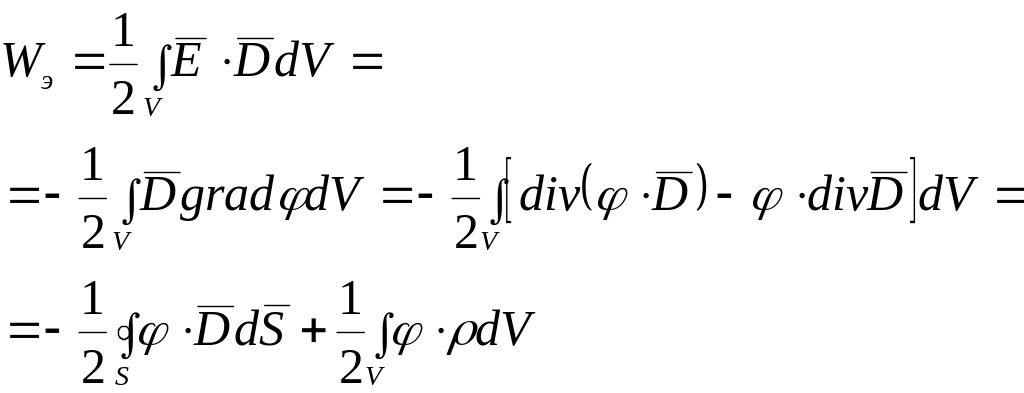
по теореме Остроградского-Гаусса.

Интегрируем по всему объему, где есть поле, исключая проводники, так как поле внутри них равно нулю. Интеграл по замкнутой поверхности распадается на 2 интеграла:

1. Интеграл по поверхности металла;

2. Интеграл по бесконечности.

, т. к. быстрее, чем



Уравнение (2) указывает на то, что в каждом элементе объема есть некая плотность энергии . Уравнение (1) об этом ничего не говорит. Это энергия взаимодействия зарядов. Следовательно, уравнение (1) имеет смысл для потенциального поля, а уравнение (2) имеет смысл всегда.

Таким образом

Первое равенство говорит о том, где сосредоточена энергия, а последнее слагаемое последнего равенства не говорит об этом ничего.

Если есть какое-то тело в поле, то найдем силу, с которой поле действует на это тело. Дадим телу некоторый элемент перемещения . Тогда на это перемещение будет затрачена определенная работа:

- принцип возможных перемещений.

Мы затратили энергию источника. Баланс энергий:

Энергия источника расходуется на увеличение энергии поля и на совершение работы.







Половина энергии идет на увеличение поля и половина – на механическое перемещение при условии

Если все тела изолированы и , и отсоединены от источника, то механическая работа производится за счет убыли энергии электрического поля:



Проведем аналогию поля в диэлектрике и в проводящей среде..

	Электрическое поле,	Поле постоянных токов при
1	, ,	, ,
2
3
4
5
6
7

Из таблицы видно, что если заменить определенные параметры друг на друга ( , , ), то уравнения будут одни и те же.

На этом принципе основано моделирование полей. Если задача решена в электростатическом поле, то решать ее в проводящей среде не надо, а нужно в старом решении заменить все величины по аналогии.

Поле в несовершенных диэлектриках.

Будем рассматривать реальные среды. Пусть поля меняются во времени достаточно медленно. Будем считать, что электрическое поле меняется так медленно, что возникающее магнитное поле не искажает электрическое и наоборот, т. е. форма поля такая же, как и для постоянных полей. В этом случае уравнения максвелла имеют вид:

Рассмотрим - не является функцией координат:

Если взять поле постоянных токов, то

Т. е. в поле постоянных токов при условии, что параметры среды не являются функцией координат, то объемные заряды существовать не могут.

Рассмотрим - является функцией координат:

по закону сохранения зарядов (дифференциальное уравнение для объемной плотности заряда)

Пусть в некоторой области (среде) могут накапливаться свободные заряды, т. к. есть проводимость. Если неоднородной среды нет, то уравнение показывает, что если там и были заряды, то они рассасываются.

Так как

Обозначим , где - время релаксации.

Тогда .

В установившемся режиме

показывает постоянную времени, с которой будет разряжаться конденсатор, отключенный от источника. Для хороших диэлектриков достигает нескольких часов.

Процессы, связанные через несовершенные диэлектрики, происходят медленно, по сравнению с процессами, которые происходят в линиях и цепях. Процессы, связанные с распределением зарядов через несовершенные диэлектрики, очень медленные.

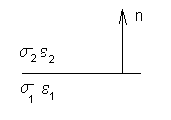
Рассмотрим граничные условия.

Пусть мы имеем установившийся режим:



Электрические свойства и параметры среды.

Если мы имеем несовершенный диэлектрик, то .

Если режим синусоидальный, то надо вводить комплексные параметры:

В общем случае, если материал обладает вязкостью, то является комплексной величиной: .

- эквивалентная проводимость.

Если относительная диэлектрическая проницаемость тоже комплексная, то:

- характеризует поглощение активной мощности. В экспериментах обычно не удается разделить и , поэтому пишут:

, где ,

Вместо эквивалентной проводимости можно ввести эквивалентную относительную диэлектрическую проницаемость.

;

- плотность полного тока в поле несовершенного диэлектрика.

всегда, т. к. вектор полного тока не имеет источников.

Если решение в установившемся синусоидальном режиме известно, то имеем дело с комплексами и виды уравнений такие же, как для постоянных полей (поля очень медленно меняются). Магнитное поле не наводит заметное электрическое поле, т. е. старое электрическое поле, которое породило магнитное поле, не изменяется:

Поле остается потенциальным  распределение поля будет таким же, как и в случае постоянного поля, если все свободные и связанные заряды фиксируются в данное мгновенное значение. Если решать задачу, то надо взять решение в постоянном поле и подставить туда комплексные вектора и параметры среды.