- •Основы теории электромагнитного поля. Основные законы электромагнитного поля в интегральной форме.
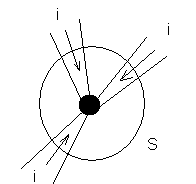
- •1. Закон сохранения зарядов.
- •2. Теорема Гаусса.
- •Закон магнитной индукции.
- •Закон полного тока.
- •Закон электромагнитной индукции.
- •Дифференциальные законы электромагнитного поля.
- •Законы Максвелла в дифференциальной форме.
- •Закон сохранения зарядов:
- •Первое уравнение Максвелла.
- •Второе уравнение Максвелла.
- •4. Теорема Гаусса.
- •Получим из уравнения № 2 уравнение № 3.
- •Получим из уравнения № 1 уравнение № 4.
- •Уравнения электромагнитного поля в комплексной форме
- •Электромагнитное поле в поляризующейся среде.
- •Электростатическое поле.
- •Рассмотрим семейство силовых линий.
- •Поле электрического диполя.
- •Электрическое поле в проводящей среде.
- •Энергия и силы в электрическом поле.
- •Магнитное поле.
- •Рассмотрим связь между векторами: .
- •Скалярный потенциал магнитного поля.
- •Собственная и взаимная индуктивность.
- •Энергия магнитного поля.
- •Вопрос о силах, действующих в магнитных полях.
- •Переменное электромагнитное поле.
- •Теорема Умова – Поинтинга.
- •Рассмотрим вопрос о комплексных параметрах среды.
- •Теорема Умова – Поинтинга в комплексной форме.
- •Электродинамические потенциалы.
- •Рассмотрим электромагнитное поле в проводящей среде.
- •Переменное поле в идеальном диэлектрике.
- •Понятие об излучении энергии.
- •Электромагнитное поле элементарного излучателя.
- •Основные свойства свч – диапазона.
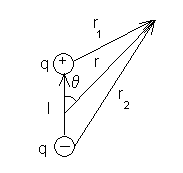
Поле электрического диполя.
|
Если
|
![]() и
и
![]() ,
тогда
,
тогда
![]() - убывает быстрее,
чем
- убывает быстрее,
чем
потенциал точечного заряда.
Если
- известно, то найдем
![]() :
:
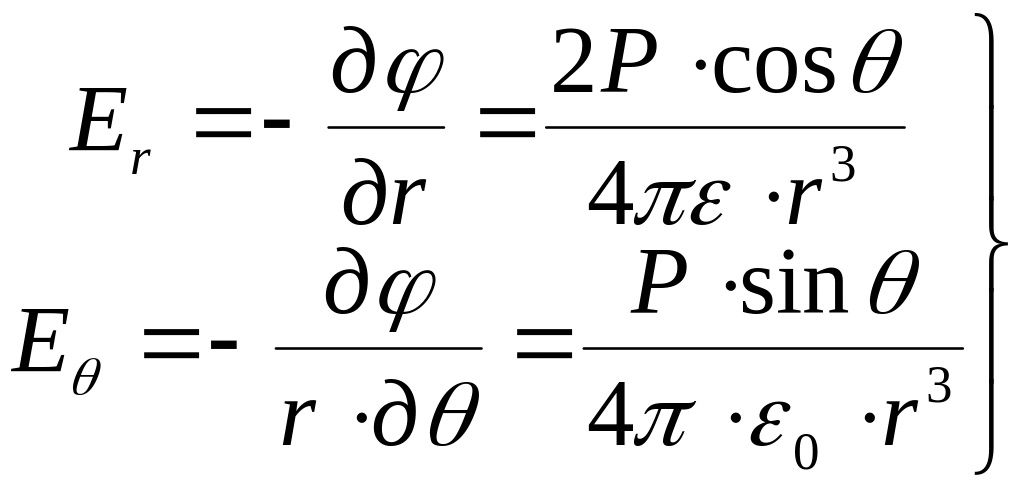 - убывает быстрее,
чем точечный заряд.
- убывает быстрее,
чем точечный заряд.
Внешнее поле действует на диполь с силой. Найдем эту силу.
|
Полагаем, что l
мало. Сила
действующая на диполь:
Если
|
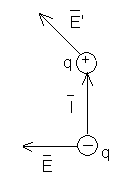
Если вектор поляризации и вектор напряженности электрического поля параллельны друг другу, направлены в одну сторону или в противоположные стороны, то положение устойчивое, поскольку момент силы равен нулю.
Если после прихода в положение равновесия диполь имеет возможность двигаться, то он будет двигаться туда, где напряженность электрического поля больше.
Электрическое поле в проводящей среде.
Уравнения Максвелла можно записать в виде:
![]()
![]()
![]()
![]()
![]()
Поле потенциально, если отсутствуют посторонние силы в проводящей среде.
![]()
Это следует из
закона сохранения зарядов в дифференциальной
форме для
![]() .
.
Если проводимость
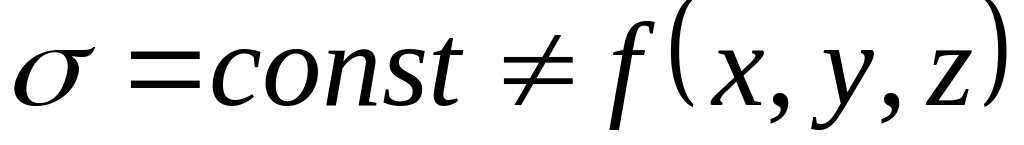 ,
а
,
а
![]() ,
то если
,
то если
![]()
![]() - закон Ома в
дифференциальной форме.
- закон Ома в
дифференциальной форме.
![]()
Тогда, потенциал поля удовлетворяет уравнению Лапласа.
![]()
Покажем, что все законы в интегральной форме легко получаются из этих уравнений. Например:
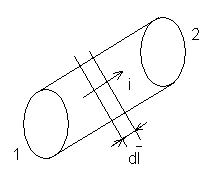
Закон Ома.
|
т. к.
|
![]()
![]() - закон
Ома в дифференциальной форме.
- закон
Ома в дифференциальной форме.
Закон Джоуля-Ленца:
![]() - дифференциальная
форма
- дифференциальная
форма
![]() - интегральная
форма
- интегральная
форма
![]()

=0 (в нашем случае)
![]()
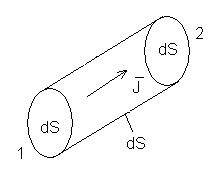
|
По теореме Остроградского-Гаусса:
На боковой поверхности:
- закон Джоуля-Ленца в интегральной форме. |
Законы Кирхгоффа:
|
По теореме Остроградского-Гаусса возьмем поверхностный интеграл и охватим этой поверхностью узел, из которого вытекают или в который втекают токи.
|
![]() - первый закон
Кирхгофа в интегральной форме.
- первый закон
Кирхгофа в интегральной форме.
,
![]()
![]()
![]() - второй закон
Кирхгофа в интегральной
- второй закон
Кирхгофа в интегральной
форме.
![]()
Если
![]() ,
то
,
то![]()
Если
![]() ,
второй закон Кирхгоффа имеет вид:
,
второй закон Кирхгоффа имеет вид:
![]() (с учетом изменения
магнитного потока во времени)
(с учетом изменения
магнитного потока во времени)
![]()
![]()
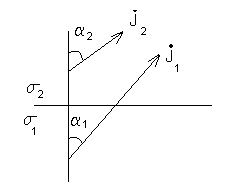
Перейдем к граничным условиям. Пусть имеется граница раздела двух сред.
Для изотропных
тел:
![]()
|
|
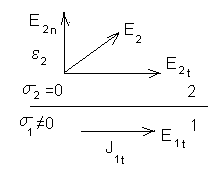
Рассмотрим диэлектрик.
![]() (это следует из предыдущего случая)
(это следует из предыдущего случая)
|
|
В диэлектрике у поверхности проводника вектор напряженности электрического поля не нормален, а расположен под углом это не эквипотенциаль.