Уравнения электромагнитного поля в комплексной форме

Наши уравнения справедливы для любой зависимости от времени, тогда рассмотрим их для синусоидальной зависимости. Введем комплексный вектор:

Вектор синусоидально изменяется во времени, если каждая из его составляющих синусоидально изменяется во времени.

Пусть:

Если , то вектор не меняет свое направление.

Если , то вектор меняет свое направление, так как если одна составляющая равна нулю, то другая не равна нулю и т.д.

Конец вектора описывает эллипс, а его модуль не синусоидально изменяется.

Выразим все в комплексах:

Тогда:

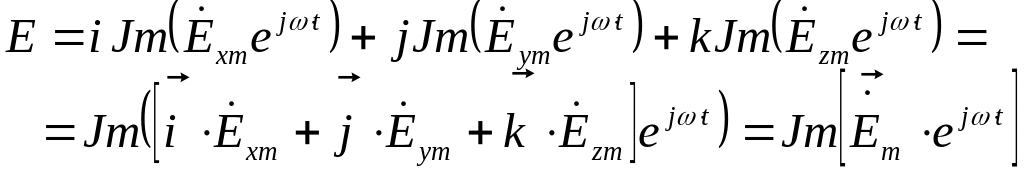
Здесь:

Запишем первое уравнение Максвелла:

Здесь равенство мнимых частей и, следовательно, комплексы равны:

Запишем второе уравнение Максвелла:

,

аналогично:

Запишем третье уравнение Максвелла:

,

аналогично:

Запишем четвертое уравнение Максвелла:

аналогично:

Мы избавились зависимости параметров поля от времени, введя комплексы. В этом суть введения комплексного метода!

Электромагнитное поле в поляризующейся среде.

Если в поле есть поляризующая среда (диэлектрики), то молекулы вещества поляризуются. Есть два типа поляризаторов (см. курс физики).

По теореме Гаусса: (для вакуума)

Если есть диполи, то:

Можно эти заряды учесть и так:

Пусть - дипольный момент единицы объема.

вектор направлен от минуса к плюсу.

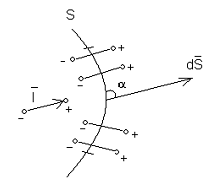
Пусть имеется кусок замкнутой поверхности S. Пусть число диполей в единице объема равно . Заряд каждого диполя равен , тогда заряд единицы объема равен

Пусть угол между вектором и вектором равен , тогда:

Если поле действует в таком направлении, то если - острый угол, то плюс (+) совпадает с нормалью и следовательно возникает минус (-).

Для замкнутой поверхности S будет:

Подставляя получим:

или:

Обозначив

, получим:

- вектор электрического смещения и это есть его определение.

Введя этот вектор мы можем сразу найти сумму свободных зарядов.

Если мы проделаем следующую операцию:

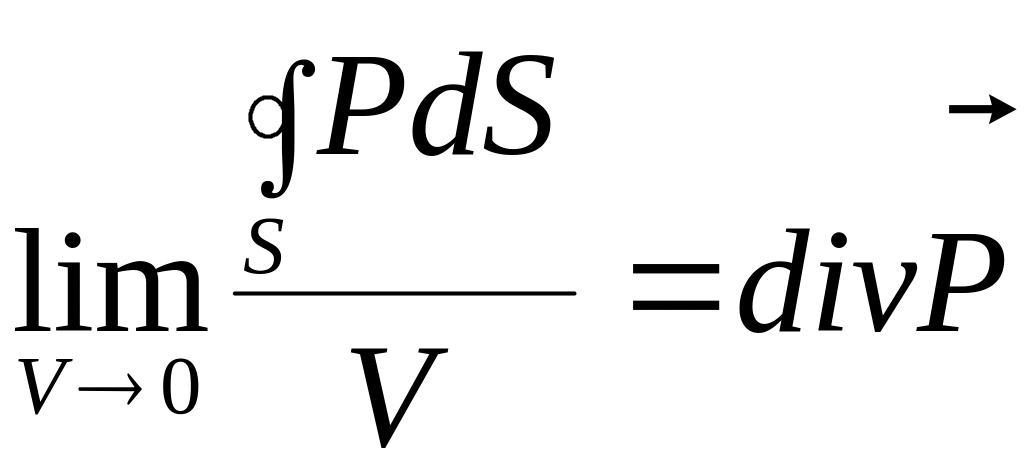
и по определению:

или

Перейдя к пределу получим уравнение в дифференциальной форме:

Если , то линии вектора могут начинаться и кончаться на зарядах, а линии вектора могут кончаться и начинаться на связанных зарядах. Источником линий вектора будут как связанные, так и свободные заряды.

Соотношение справедливо всегда, даже если она вызвана не электрическим воздействием.

Можно сказать, что при не очень сильных полях:

- диэлектрическая восприимчивость, тогда:

, откуда:

- частный случай.

Возникает вопрос о том, как учесть то, что поляризация следует не сразу за приложением электрического поля?

Это можно учесть уравнением вязкости:

,

где - постоянная величина.

Скорость изменения поляризации пропорциональна разности между каким – то значением и поляризацией в данный момент времени (истинной поляризацией).

Если процесс установился, то ,

следовательно величина - поляризация установившаяся при данном значении .

Так как все величины конечны, то конечно и, следовательно, вектор меняется плавно без скачков, а вектор - может делать скачки.

Пусть режим синусоидальный:

, следовательно:

, следовательно:

, обозначим

- комплексная восприимчивость, следовательно, вектора и не совпадают, то есть поляризация запаздывает по фазе.

Введем

, следовательно:

, т. е. вектор будет отставать от вектора

Пусть частота невелика (маленькая):

, то - поляризация успевает за изменением поля.

, то - в вакууме настолько быстро изменяется поле, что поляризация не успевает даже среагировать, т. е. поляризация отсутствует и среда ведет себя как вакуум.