Получим из уравнения № 2 уравнение № 3.
Если в начальный момент , то она все время будет равна нулю, так как не зависит от времени.
Получим из уравнения № 1 уравнение № 4.
,
так как
,
то:
но по закону сохранения зарядов:
следовательно:
,
или
В два первых уравнения входят пять (5) векторов – зависимых друг от друга:
-
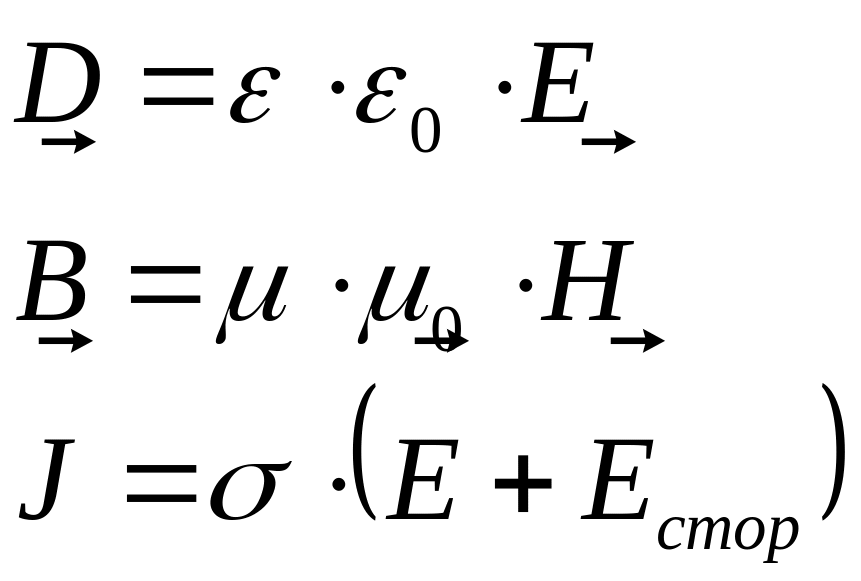
удельная проводимость, а последнее
равенство – закон Ома в дифференциальной
форме.
Эти соотношения справедливы только тогда, когда мы имеем линейные среды!
На самой границе двух сред векторы меняются скачком. Возникает вопрос, а какой вид принимают наши уравнения на границе 2-х сред?
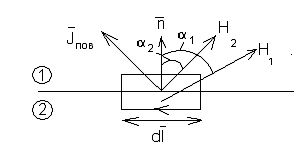
Пусть имеется
граница двух сред 1 и 2. Выберем контур,
вертикальные стороны которого очень
малы. Введем поверхностную плотность
тока – конечный ток в бесконечно тонком
слое (
).
|
Первое уравнение Максвелла имеет вид:
или:
|
Применим уравнение к этому контуру:
На верхней стороне
будет
,
на вертикальной стенке интеграл равен
нулю, так как он бесконечно мал по
сравнению с горизонтальной стенкой,
следовательно, необходимо определить,
чему равна разность тангенциальных
составляющих?
Объемные токи будут стремиться к нулю из-за стремления к нулю вертикальных стенок, следовательно:
,
где N – нормаль к площадке, а не к поверхности, откуда
граничное условие
для тангенциальных составляющих
напряженности магнитного поля.
Если
Если
- нормаль к поверхности раздела двух
сред, тогда:
Перейдем сразу к третьему уравнению Максвелла:
|
,
или
Пусть высота
параллелепипеда стремится к нулю,
тогда поток через верхнюю стенку равен
|
,поток
через нижнюю стенку равен -
Откуда:
,
следовательно:
это верно всегда!
Можно записать и
так:
Вектор непрерывный и следовательно нормальные составляющие не делают скачков, т.е. они равны.
Теперь рассмотрим второе уравнение Максвелла:
|
или
;
|
,
так как площадка стремится к нулю,
следовательно:
- это граничное
условие для вектора
верно всегда.
Рассмотрим четвертое уравнение Максвелла:
|
или:
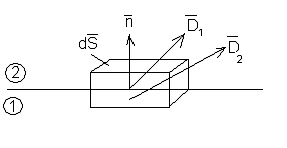
На поверхности
раздела есть поверхностные заряды,
т.е. существует
поверхностная плотность
зарядов (
|
)Следовательно, проводя аналогичные рассуждения, можно записать:
,
или
- граничные условия нормальной составляющей
вектора электрического смещения
.
Если
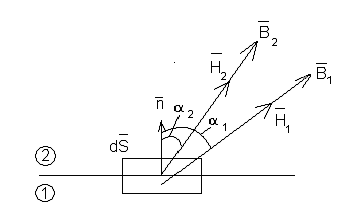
Запишем два ранее выведенных граничных условия:
(1)
(2)
Разделим первое равенство на второе, получим:
,
или:
,
или:
- условие преломления
линий на границе, только при определенных
условиях
Аналогично:
при условии
Мы говорим, что вектор полного тока непрерывен, следовательно:
, или:
,
отсюда получим по аналогии с
