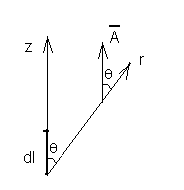
Электромагнитное поле элементарного излучателя.
Элемент проводника обтекаемый переменным током – элементарный излучатель.
|
Будем считать,
что ток одинаков по всей длине
Куда он на концах девается? Это можно представить в виде диполя Герца. Применим сферическую систему координат. Будем считать поле плоско меридианное.
|
Для диполя будет:
В комплексной форме:
Воспользуемся уравнением для векторного потенциала:
Рассмотрим
синусоидальный режим
Если векторный потенциал известен, то можно определить напряженности магнитного и электрического поля
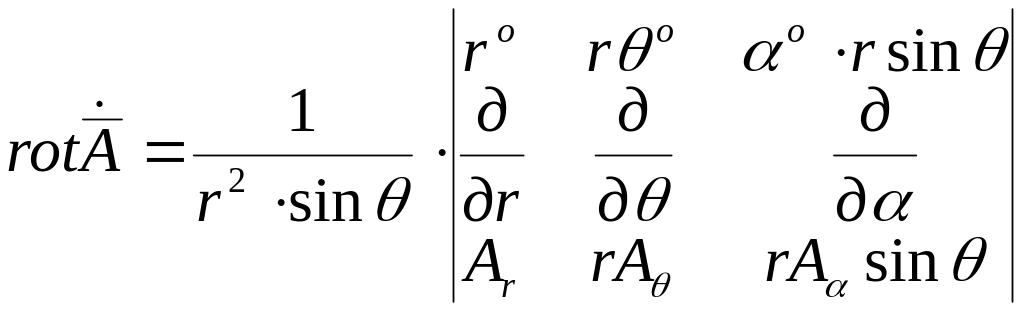имеется только
-
составляющая:
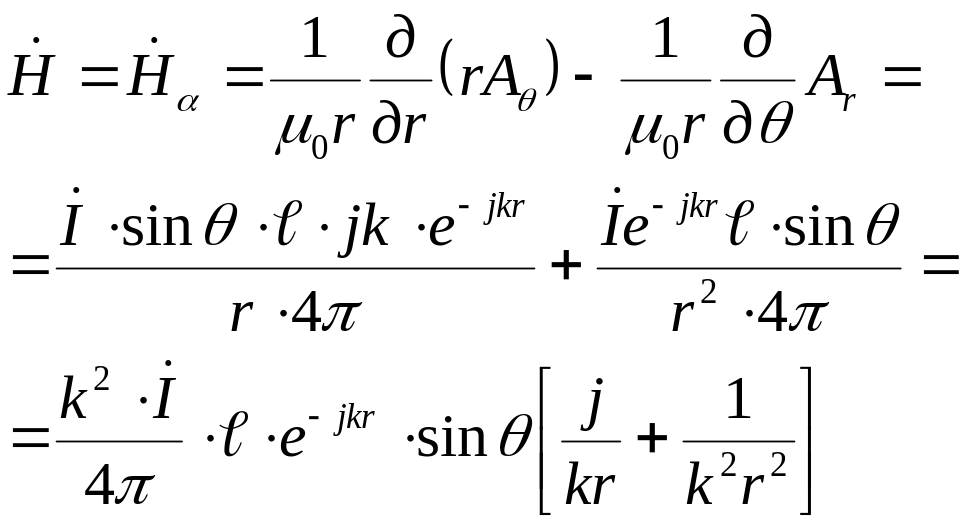
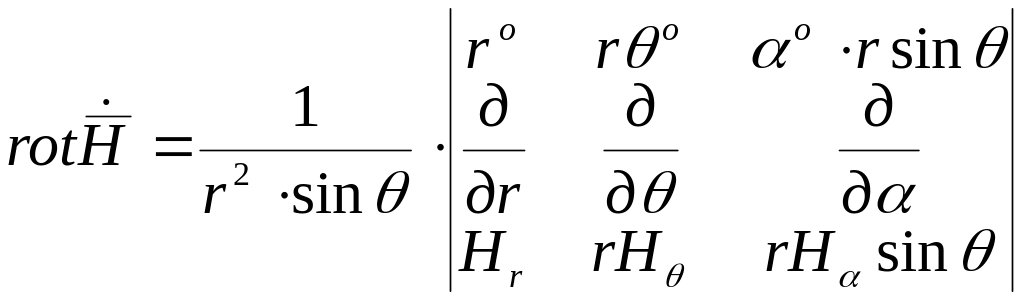имеется только
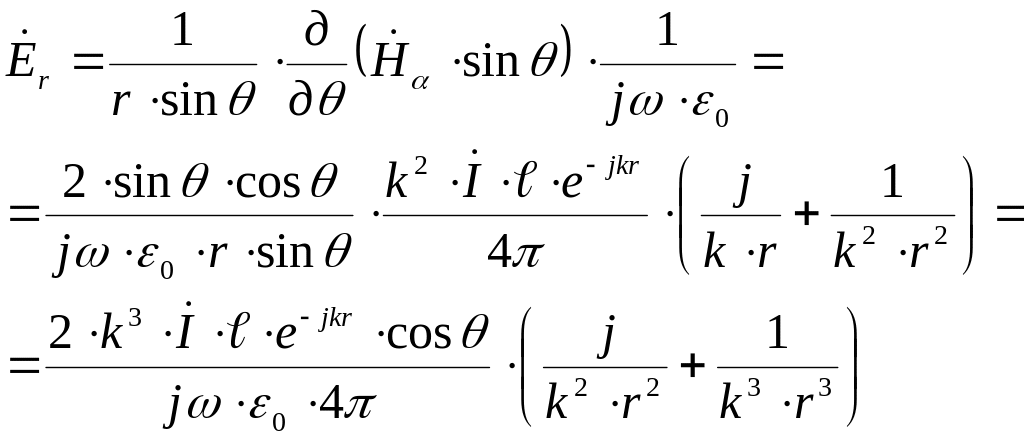
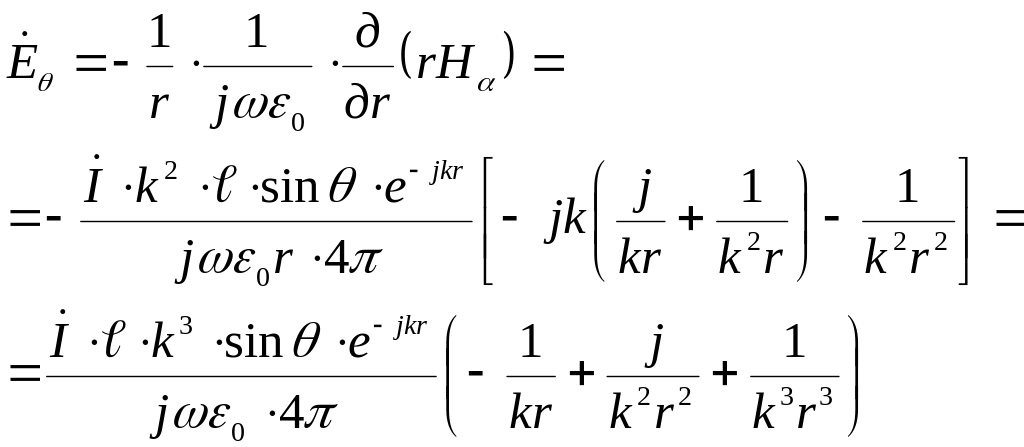
(это следует из
ротора)
В общем случае вектор напряженности магнитного поля перпендикулярен меридианной плоскости и следовательно вектора напряженности магнитного поля расположены по параллелям.
Вектор напряженности электрического поля лежит в меридианной плоскости и перпендикулярен вектору напряженности магнитного поля.
Вектора
напряженности электрического и магнитного
поля являются функциями радиуса и угла
,
причем от угла зависимость синусоидальная.
Множитель
соответствует запаздыванию, а в скобках
зависимость амплитуды и фазы от радиуса.
,
из этого соотношения видно, что вектора
ведут себя по-разному в разных областях.
Ближняя зона – квазистационарная зона.
В этой зоне
,
то есть рассматривается поле на расстоянии
от диполя на
В этом случае
уравнения упростятся:
- определяем по
закону Био-Савара:
т.е. это выражение
для элемента тока, определенное как для
постоянного тока по закону Био-Савара
У нас было
,
тогда:
Это поле
диполя, мы его уже получали с моментом
,
определенного так как и для постоянного
поля, то есть в данной точке мгновенные
значения эквивалентны постоянному
полю.
Следовательно, форма поля не меняется, так как формулы одни и те же, а они и определяют картину поля. Таким образом, поле меняется со временем, но картина одна и та же. Следовательно, поле – квазистационарное.
Напряженности
электрического поля
и
по фазе совпадают, но с вектором
напряженности
- расположены под углом
.
Это приводит
к тому, что вектор Поинтинга
- является чисто мнимой величиной.
- это выражение не
будет иметь в ближней зоне активной
составляющей, так как сдвиг фазы в
,
то есть активная мощность не излучается!
На самом деле это не так!
Если мы пренебрегаем малыми слагаемыми, то мы пренебрегаем и излучением, так как оно определяется отброшенными слагаемыми. По этим формулам мы только определяем картину поля, а определить вектор Поинтинга нельзя.
Дальняя зона – волновая зона.
,
так как в дальней зоне
,
Для будет:
Таким образом, в дальней зоне вектор напряженности магнитного поля имеет только одну составляющую и вектор напряженности электрического поля тоже имеет одну составляющую.
Отсюда вектор
Поинтинга имеет только одну составляющую
.
В дальней зоне амплитуда убывает обратно пропорционально первой степени расстояния, и напряженности векторов магнитного и электрического поля зависят синусоидально от угла
Если
Все эти соотношения справедливы для дальней зоны. В этой зоне у нас получилась сферическая волна. Поверхность равной фазы – поверхность равного радиуса. В дальней зоне волны сферические
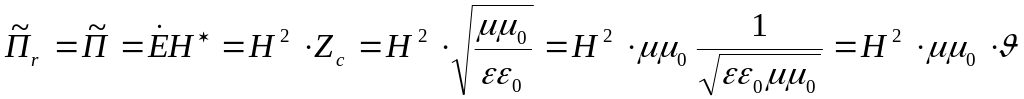
Можно тоже самое
проделать и вектора напряженности
электрического поля и получить
Следовательно:
Или:
Направление скорости распространения энергии совпадает с фазовой скоростью:
Если вектора напряженности электрического и магнитного поля совпадают по фазе, то вектор Поинтинга никогда не бывает отрицательной величиной, то есть энергия всегда идет от диполя и никогда не возвращается в диполь. Это только для дальней зоны.
Возникает вопрос, а какая мощность излучается диполем?
|
|
Рассмотрим выражение
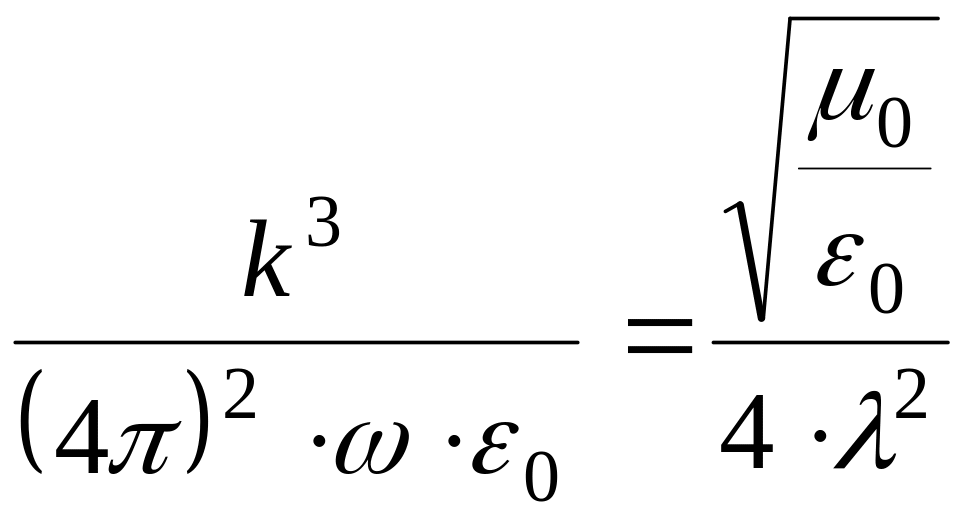
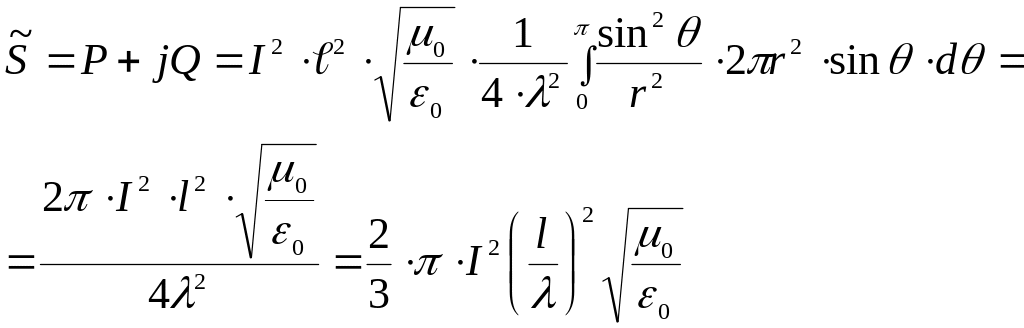
С учетом
можно записать:
,
тогда
Если сопротивление излучения умножить на квадрат тока, то мы получим излучаемую мощность.
Вектор Поинтинга для ближней зоны чисто реактивный, а в дальней зоне мощность излучается. Кажется, что нарушается теорема Умова-Поинтинга. На самом деле не нарушается.
Для этого рассмотрим, какая мощность выходит из некоторого объема вне зависимости от того, в какой зоне мы находимся. Надо рассмотреть точное выражение.
В общем случае вектор Поинтинга будет иметь две составляющие действительную часть и мнимую.
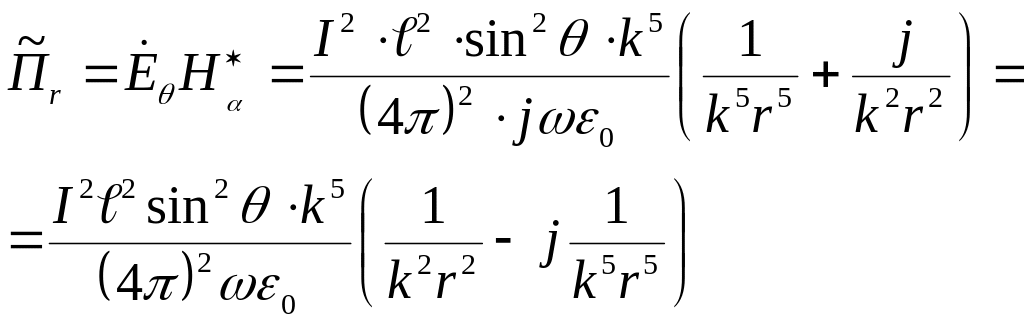
Мы получили, что вектор Поинтинга в любой области имеет две составляющие. Первое слагаемое сравнительно медленно убывает с ростом радиуса, а второе слагаемое убывает значительно быстрее. Реактивная составляющая имеет емкостной характер (-j).
Чем дальше мы находимся от диполя, тем меньше реактивная составляющая по сравнению с активной.
Вектор Поинтинга уменьшается как квадрат радиуса, а поверхность растет как квадрат радиуса, следовательно величина мощности не меняется, т.е. активная мощность на любом расстоянии не зависит от радиуса, а реактивная мощность:
Поэтому, когда говорим, что вектор Поинтинга равен нулю в ближней зоне, то это неверно, так как мы не учитываем малые составляющие, а именно они и определяют вектор Поинтинга.
СВЧ – техника.