Рассмотрим электромагнитное поле в проводящей среде.

Исходим из уравнений Максвелла:

(1)

(2)

1. рассматриваем линейные среды

2. рассматриваем однородные среды

3. сравнительно хорошие проводники, следовательно, токами смещения можно пренебречь по сравнению с током проводимости и следовательно уравнения (1) и (2) – упрощаются:

(1)

(2)

Сведем к одной неизвестной:

Для проводящей среды первое слагаемое равно нулю, так как свободных зарядов нет и , следовательно и

, так как параметры среды не зависят от координат, или:

, т.е. внутри проводника заряды существовать не могут.

- уравнение для вектора напряженности электрического поля в проводящей среде.

- уравнение для вектора напряженности магнитного поля.

Эти два уравнения диффузии или уравнения теплопроводности с точки зрения математики (математической физики).

На практике почти всегда используют синусоидальный режим:

В этих уравнениях величина

Если

Никаких ограничений на эти уравнения мы не накладываем.

Переменное поле в идеальном диэлектрике.

Идеальный диэлектрик:

Уравнения Максвелла имеют вид:

Тогда:

,

Здесь:

,

Следовательно:

или

Аналогично можно получить:

Плоская волна – простейший случай, когда векторы поля зависят только от одной координаты.

Плоско-поляризованная волна - когда вектор находится все время в одной плоскости (имеет только одну составляющую по осям).

Понятие об излучении энергии.

Если соблюдается условие: , тогда:

Возникает вопрос о том, как решить эти уравнения?

Давайте найдем сферически симметричное решение уравнения:

Они одинаковы и следовательно, решим скалярное уравнение – оно проще.

Пусть имеется некий объем , где есть заряды, изменяющиеся во времени. Вне этого объема зарядов нет. Следовательно:

Рассмотрим поле этого объема. В этом объеме поле удовлетворяет неоднородному уравнению, а в окружающем пространстве – однородному уравнению:

Сферическая симметрия означает, что зависимость только от радиуса и других параметров не зависит, так как в дали, источник считается точечным.

Лапласиан в сферической системе координат можно записать в виде:

Как решить это уравнение? Ведем обозначения: , тогда:

Откуда:

, тогда: - уравнение в лучшем виде.

Это уравнение имеет решение:

, т.е. мы получили сумму двух волн

1. первая волна распространяется в сторону положительных значений

2. вторая волна распространяется навстречу в сторону отрицательных значений .

Если , т.е. точка, в которой первая функция не меняется, движется со скоростью света .

Вторая волна которая распространяется навстречу не имеет смысла, так как мы считаем, что вне нашего объема зарядов нет и следовательно нет и внешней волны:

Возникает вопрос о том как найти функцию ?

Для постоянного поля нам известна эта функция:

Для переменного поля будет отличие: , следовательно:

Для определения потенциала в точке надо брать время на некоторое время предшествующее – это время - это тогда, когда мы определяем потенциал в точке наблюдения. Надо, чтобы волна прошла путь , следовательно, это запаздывающие потенциалы.

Вывод: поле возбуждается и распространяется не мгновенно. Электродинамические потенциалы – это запаздывающие потенциалы. Т. е. мы доказали это только для потенциала . Это справедливо только для потенциала. Для векторов поля – это не верно.

В общем случае:

, следовательно:

Плотность заряда и ток связаны между собой законом сохранения заряда

в этом соотношении я могу (линейные токи) для тонких проводников заменить: , тогда для линейных проводников

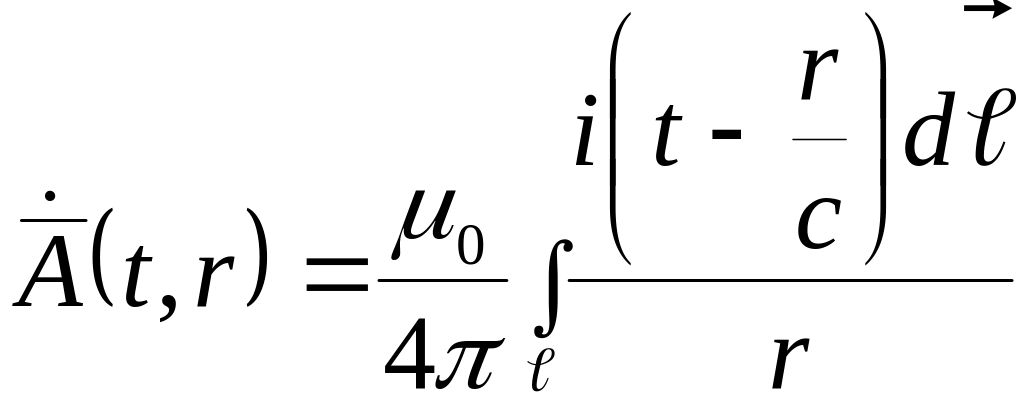
Пусть , тогда:

,

где:

Если применим комплексный метод, то: