Переменное электромагнитное поле.
Основные уравнения Максвелла:
Теорема Умова – Поинтинга.
Качественные
рассуждения:
пусть имеется некоторый объем
,
ограниченный поверхностью
.
В этом объеме могут быть сторонние
источники и за время
может совершаться работа.
Согласно закону сохранения энергии:
т.е. за счет
сторонних источников совершается
работа, которая связана с преобразованием
в тепло, в изменение энергии электромагнитного
поля и убыли энергии через поверхность,
которая охватывает рассматриваемый
объем.
Энергия есть квадратичная функция.
(1)
(2)
Уравнение (1) умножим на вектор напряженности электрического поля , а уравнение (2) умножим на вектор напряженности магнитного поля . Теперь вычтем из уравнения (1) уравнение (2), получим:
,
Тогда:
Возьмем интеграл по объему, чтобы получить всю энергию:
Введем обозначение:
,
тогда по теореме Остроградского –
Гаусса:
Качественные рассуждения:
- мощность всех
сторонних источников в объеме
- удельная мощность,
выделяемая в объеме с которой энергия
превращается в тепло
- энергия
электромагнитного поля во всем объеме
- та мощность, с которой возрастает
энергия электромагнитного поля во всем
объеме
Тогда остается:
(качественно) –
эта мощность представлена как интеграл
по поверхности от вектора и равна потоку
вектора через эту поверхность.
Поток вектора
через поверхность
,
ограничивающую объем
- называется вектором Поинтинга.
Вектор - показывает величину и направление распространяющейся энергии, сколько мощности проходит через единичную площадку, ориентированную нормально к направлению этого вектора.
Рассмотрим вопрос о комплексных параметрах среды.
Если нас не интересуют эффекты нелинейности, то из-за потерь вектор не совпадает по фазе с вектором .
Заменяя не синусоидальную кривую эквивалентной синусоидальной, можно представить
Вводя уравнение вязкости для магнитной среды
,
где
- вектор намагниченности
Для синусоидального режима будет:
Введем параметр
- комплексная восприимчивость
Введем
- является функцией частоты.
Теорема Умова – Поинтинга в комплексной форме.
Введем аналогичным
образом
,
тогда можно записать
Пойдем теперь обратным путем, допустим, что надо определить мощность входящую внутрь какого-то объема:
По теореме Остроградского – Гаусса для синусоидального режима:
Но
Кроме того, 2-е и 1-е уравнения Максвелла можно записать в виде:
Подставим эти уравнения в исходное выражение
Раскроем выражение
в скобках с учетом, что:
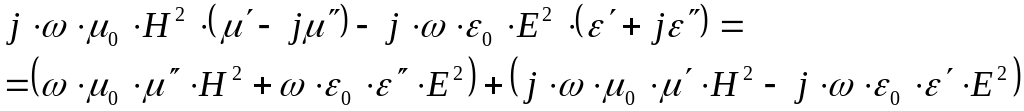
Следовательно:
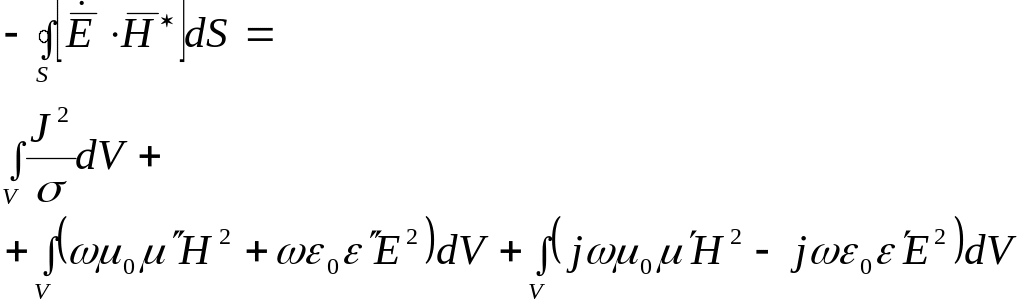
Или (одно и то же):
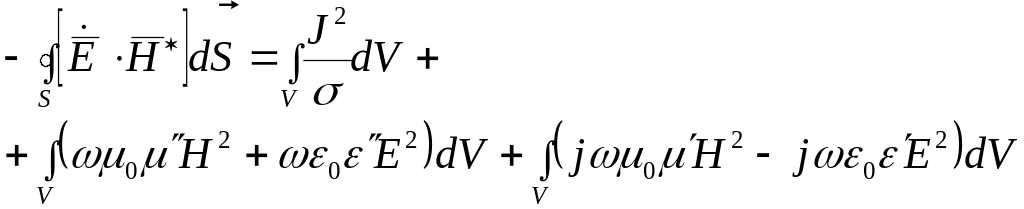
Мощность преобразовывается из-за Джоулевого тепла, тепла из-за диэлектрической и магнитной вязкости среды, а реактивная мощность – это просто расчетная величина.
- потери магнитной
вязкости на единицу объема
- потери
диэлектрической вязкости на единицу
объема
Это закон сохранения активной и реактивной мощности
Электродинамические потенциалы.
Нельзя ли в переменном электромагнитном поле ввести потенциал?
У нас есть уравнение
Запишем исходные уравнения поля:
;
;
Известно, что
,
подставим во 2-е уравнение
,
следовательно, для переменного поля
справедливо общее выражение:
Найдем дифференциальные уравнения, которым этот потенциал удовлетворяет. Для этого воспользуемся уравнениями (1) и (4)
Известно, что
Тогда
Воспользуемся
произволом выбора
и
с целью упрощения уравнения
Пусть
,
тогда
- дифференциальное
уравнение, которому удовлетворяет
векторный потенциал. Это неоднородное
векторное волновое уравнение – называется
уравнение Даламбера.
Если
-
уравнение однородное
В этом уравнении содержится все, что мы с Вами изучали до сих пор.
Таким образом
(2)
(1)
Аналогия уравнения для скалярного потенциала:
Из уравнения (2)
следует:
Или:
- неоднородное
волновое уравнение
Однако здесь есть граничные и начальные условия:
Если мы задали
,
то мы задали и
,
так как
