Основы теории электромагнитного поля. Основные законы электромагнитного поля в интегральной форме.

1. Закон сохранения зарядов.

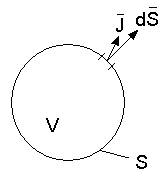
Пусть имеется некоторый объем V, ограниченный замкнутой поверхностью V, а внутри объема имеется изменяющийся во времени заряд Q.

S – замкнутая поверхность, ограничивающая объем V. Q - заряд, изменяющийся внутри объема V, ограниченного поверхностью S – плотность тока

Ток, выходящий наружу, через поверхность S равен убыванию заряда внутри данного объема V, который ею ограничен:

- закон сохранения заряда.

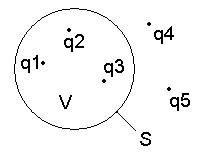
2. Теорема Гаусса.

Поток вектора через замкнутую поверхность S равен сумме зарядов внутри объема V, ограниченного поверхностью S: , где теорема Гаусса

Теорема Гаусса является следствием закона Кулона, но имеет более широкое применение, так как справедлива и для переменных полей.

3. Закон магнитной индукции.

Линии вектора - непрерывны, следовательно, магнитных зарядов в отдельности не существует.

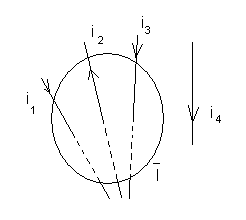
3. Закон полного тока.

- замкнутый контур - сумма токов, охваченных контуром . Положительный обход контура – правило правого винта:

где - поверхность, натянутая на контур

Линии не имеют ни начала, ни конца, следовательно, - вектор тока непрерывный и замкнутый. Такая запись учитывает только постоянное поле, а при переменном поле надо учитывать и другие токи.

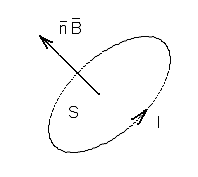
3. Закон электромагнитной индукции.

Наводимая в контуре электродвижущая сила (е) не зависит от того, чем вызван магнитный поток Ф: С другой стороны:

- электродвижущая сила обязательно возникает только в замкнутом контуре.

По определению:

Следовательно: - поверхность ограничена контуром , а знак “-” значит, что если растет вверх, то электродвижущая сила будет наводиться по часовой стрелки и наоборот.

Дифференциальные законы электромагнитного поля.

Операции 2-го порядка.

Дивергенция или расхождение какого-либо вектора определяется как предел отношения потока вектора , исходящего из замкнутой поверхности S, к объему V, ограниченному этой поверхностью, если поверхность стягивается вокруг заданной точки, для которой и определяется дивергенция:

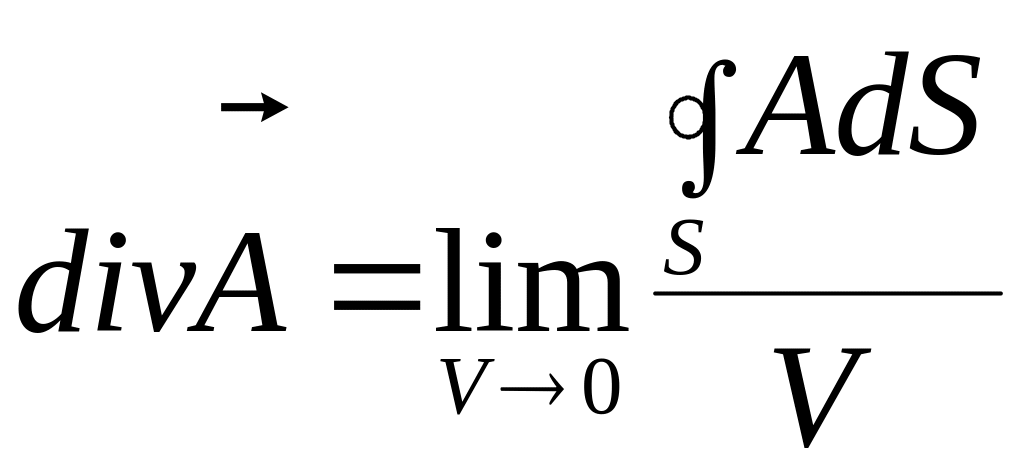
Ротор или вихрь какого-либо вектора есть вектор; его составляющая, нормальная к площадке S, определяется как предел отношения циркуляции вектора по контуру , ограничивающему площадку, к ее площади S, если контур стягивается к заданной точке, для которой и определяется соответствующая составляющая ротора:

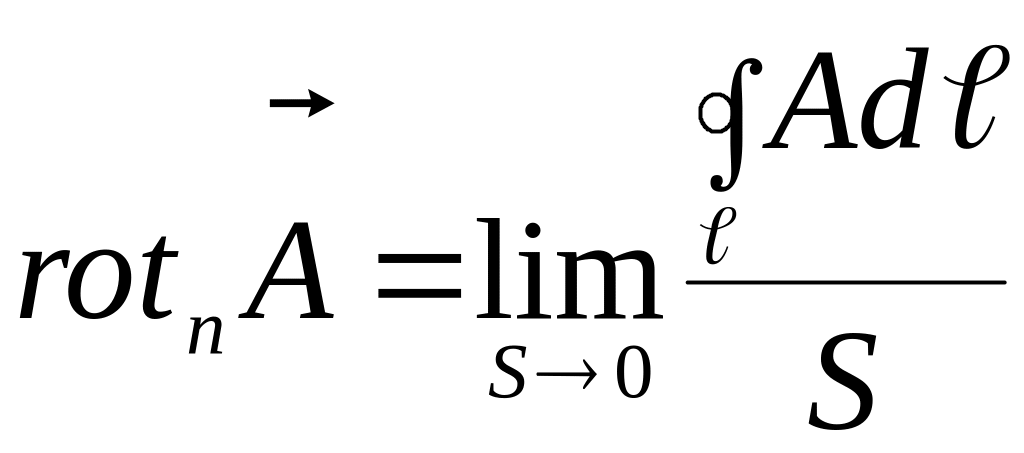
В левой части стоит принятое обозначение n-й составляющей ротора; сам вектор обозначается без всякого индекса: .

Направление нормали n к площадке S связано правилом правоходового винта с направлением обхода dl по контуру, ограничивающему S.

Градиент – это вектор, любая компонента которого равна скорости возрастания в направлении i-й координаты; направление градиента есть направление наиболее быстрого возрастания .

- оператор Набла, оператор пространственного дифференцирования – векторный оператор.

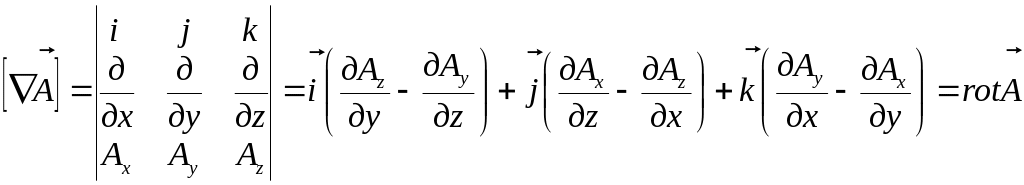
Таблица операций.

- скалярная величина