5.2. Действующее, среднее значение и мощность периодического негармонического сигнала

 

Для определенности положим, что f(t) имеет смысл тока i(t). Тогда действующее значение периодического негармонического то­ка определяется согласно (3.5), где i(t) определяется уравнением (5.10):

 

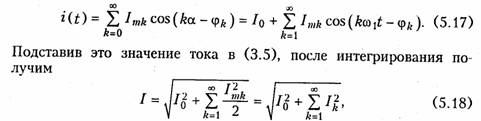
т. е. действующее значение периодического негармонического тока I полностью определяется действующими значениями его гармоник Ik и не зависит от их начальных фаз φ_k.

Аналогичным образом находим действующее значение перио­дического несинусоидального напряжения:

Среднее значение тока определяется согласно общему выра­жению (3.9). Причем обычно берут среднее значение i(t) по аб­солютной величине

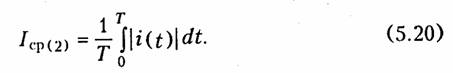
Аналогично определяется U_cp(2).

С точки зрения теории цепей, большой интерес представляет средняя активная мощность негармонического сигнала и распре­деление ее между отдельными гармониками.

Средняя активная мощность периодического несинусоидального сигнала

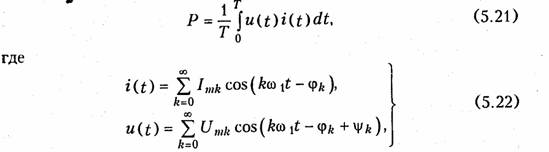
ψ_k — фазовый сдвиг между током и напряжением k-й гармоники. Подставляя значения i(t) и u(t) из (5.22) в уравнение (5.21), по­сле интегрирования получаем:

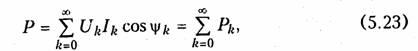
т, е. средняя за период активная мощность периодического негар­монического сигнала равна сумме мощностей отдельных гармоник. Формула (5.23) является одной из форм широко известногоравен­ства Парсеваля.

Аналогично находим реактивную мощность

Следует подчеркнуть, что в отличие от гармонических сигналов (см. (3.121)) для негармонических сигналов

6.3. Спектры периодических негармонических сигналов

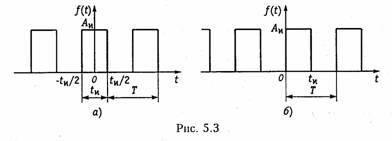
Рассмотрим последовательность прямбугольных импульсов, изображенную на рис. 5.3, а. Сигналы подобной формы находят очень широкое применение в радиотехнике и электросвязи: теле­графия, цифровые системы передачи, системы многоканальной свя­зи с временным разделением каналов, различные импульсные и цифровые устройства и др. (см. гл. 19). Импульсная последова­тельность характеризуется следующими основными параметрами: амплитудой импульса A_и*, его длительностью t_u и периодом сле­дования Т. Отношение периода Т к длительности t_иназывается скважностью импульсов и обозначается через q = Т/t_И. Обычно значения скважности импульсов лежат в пределах от нескольких единиц (в измерительной технике, устройствах дискретной пере­дачи и обработки информации), до нескольких сотен или тысяч (в радиолокации).

Для нахождения спектра последовательности прямоугольных импульсов воспользуемся рядом Фурье в комплексной форме (5.6).

Комплексная амплитуда k-й гармоники равна согласно (5.8) после возвращения к исходной переменной t.

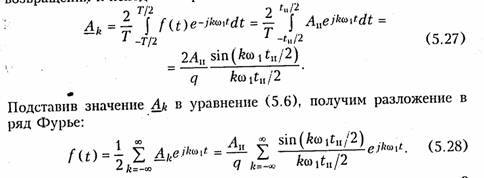
На рис. 5.4 изображен спектр комплексных амплитуд для q = 2 и q = А. Как видно из рисунка, спектр последовательности прямо­угольных импульсов представляет собой дискретный спектр с оги­бающей (штриховая линия на рис. 5.4), которая описывается функцией

носящей название функции отсчетов (см. гл. 19). Число спектраль­ных линий между началом отсчета по оси частот и первым нулем огибающей равно q —1. Постоянная составляющая сигнала (сред­нее значение) a_о/2 = A_и/q, а действующее значение А — A_u/√q, т. е. чем больше скважность, тем меньше уровень постоянной со­ставляющей и действующее значение сигнала. С увеличением скважности q число дискретных составляющих увеличивается — спектр становится гуще (см. рис. 5.4, б), и амплитуда гармоник убывает медленнее. Следует подчеркнуть, что в соответствии с (5.27) спектр рассматриваемой последовательности прямоугольных

импульсов вещественный.

Из спектра комплексных амплитуд (5.27) можно выделить ам­плитудный A_k =|A_k|и фазовый спектр φ_k = argA_k, изображенный на рис. 5.5 для случая q = 4. Из рисунков видно, что амплитудный спектр является четной, а фазовый — нечетной функцией частоты. Причем, фазы отдельных гармоник принимают либо нулевое значение между

узлами, где синус положительный, либо ±π, где синус отрицательный (рис. 5.5, б)

На  основании  формулы  (5.28)  получим тригонометрическую форму разложения в ряд Фурье по четным гармоникам (сравни с (5.15))

В случае, когда периодическая последовательность имеет разно-полярную форму (см. рис. 5.1), в спектре будет отсутствовать по­стоянная составляющая (сравните (5.30) и (5.31) с (5.14) и (5.15)).

Аналогичным образом можно исследовать спектральный состав периодических негармонических сигналов другой формы. В табл. 5.1 приведено разложение в ряд Фурье некоторых наиболее распространенных сигналов.