Случайные величины

1. В урне 6 шаров, из которых 2 черных. Наудачу вынимается 3 шара. Составить таблицу распределения вероятностей числа черных шаров среди вынутых.

2. Дана таблица распределения вероятностей случайной величины Х:

Х	4	6	8	10	12
Р	0,3	0,15	0,18	0,17	0,2

Найти математическое ожидание этой случайной величины и ее среднее квадратическое отклонение.

3. Дан закон распределения случайной величины Х:

Х	1	3	5
Р	0,3	0,2	0,5

Найти математическое ожидание, среднее квадратическое отклонение, интегральную функцию распределения F(х) и построить ее график.

4. Производятся независимые испытание трех приборов. Вероятность отказа каждого прибора соответственно равна: 0,2; 0,1; 0,3. Найти математическое ожидание числа отказавших приборов. Построить график интегральной функции распределения F(х).

5. Случайная величина Х задана интегральной функцией распределения:

F(х) =

Построить график интегральной функции распределения. Найти плотность распределения f(x) и вероятность того, что в результате испытания случайная величина Х примет значение из отрезка [1; 1,5].

6. Дана функция плотности распределения. Найти параметр а, интегральную функцию распределения случайной величины Х, ее математическое ожидание, дисперсию и среднее квадратическое отклонение.

f(x) =

7. В лотерее 10 билетов, из которых 3 выигрышных. Куплено 3 билета. Х – число купленных билетов, оказавшихся выигрышными. Составьте таблицу распределения случайной величины Х.

8. Дискретная случайная величина принимает значения: 1; 2; 3. Известны математические ожидания этой случайной величины и ее квадрата: М(Х) = 2,3, М(Х²) = 5,9. Найти вероятности, соответствующие возможным значениям Х.

Непрерывные случайные величины

1. Известна плотность распределения непрерывной случайной величины f(x). Найти:

1) параметр а,

2) функцию распределения F(x) и построить ее график;

3) вероятность попадания случайной величины Х в промежуток (,):

4) математическое ожидание и среднее квадратическое отклонение случайной величины

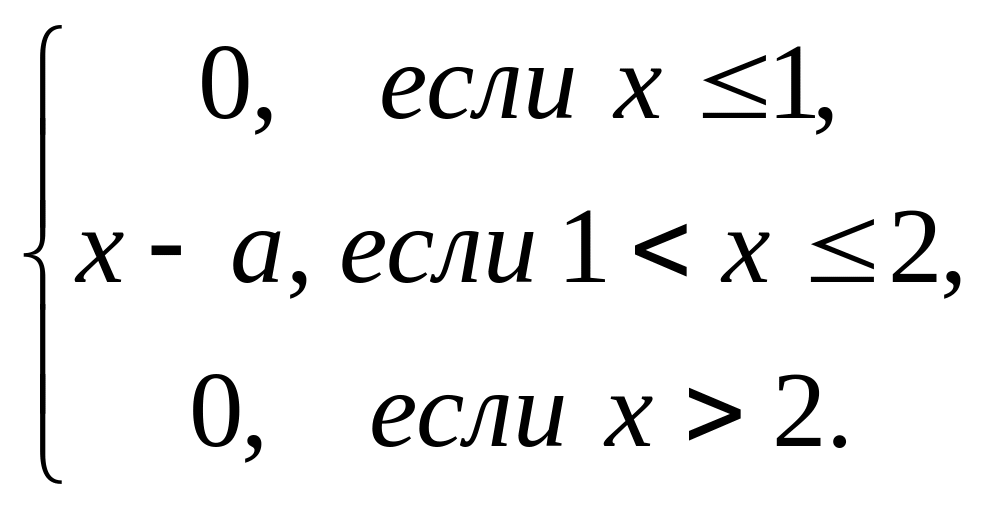
а) f(x) =  = 0,5,  = 2

б) f(x) =  = 0,  = ;

2. Случайная величина Х задана плотностью распределения f(x) = 2cos2x в интервале (0, ); вне этого интервала f(x)=0. Найти моду и медиану Х.

3. Случайная величина Х задана функцией распределения

9. F(x) =

Найти математическое ожидание, дисперсию и среднее квадратическое отклонение Х.

4. Случайная величина Х задана плотностью распределения f(x) = 0,5x в интервале (0,2); вне этого интервала f(x)=0. Найти начальные и центральные моменты первого, второго, третьего и четвертого порядков.

5. Случайная величина Х в интервале (2;4) задана плотностью распределения f(x) = х² + х – 6; вне этого интервала f(x)=0. Найти моду, математическое ожидание и медиану величины Х.

6. Найти дисперсию случайной величины Х, заданной функцией распределения:

F(x) =

Нормальное распределение

1. Математическое ожидание нормально распределенной случайной величины Х равно 2 и среднее квадратическое отклонение 2. Напишите плотность вероятности Х.

2. Изобразить схематично график плотности нормально распределенной случайной величины Х, зная, что математическое ожидание этой случайной величины равно 3, а дисперсия 16.

3. Нормально распределенная случайная величина Х задана плотностью f(х) =  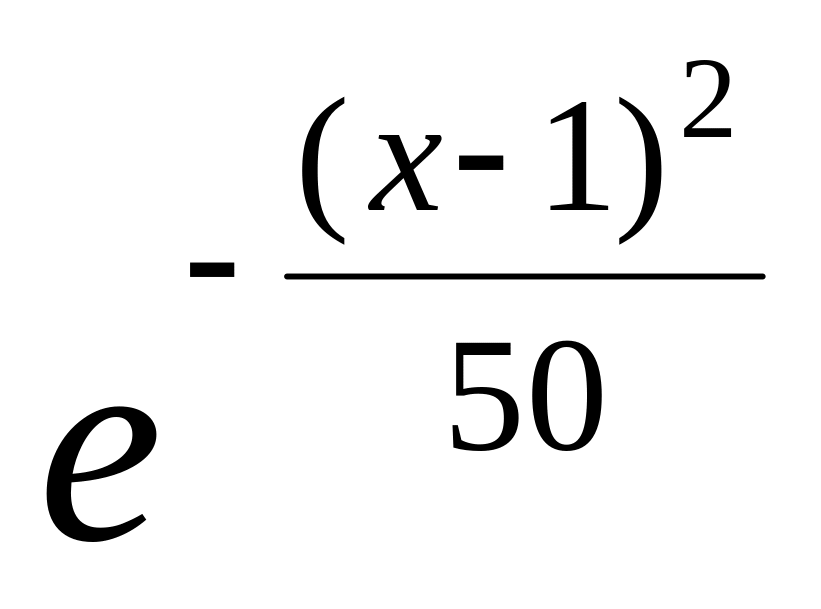. Найти математическое ожидание и дисперсию.

4. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 10 и 2. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (12,14).

5. Автомат штампует детали. Контролируется длина детали Х, которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Фактически длина изготовленных деталей не менее 32 мм и не более 68 мм. Найти вероятность того, что длина наудачу взятой детали: а) более 55 мм, б) менее 40 мм.

6. Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения Х подчинены нормальному закону со средним квадратическим отклонением 10 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15 мм.

7. Автомат изготавливает шарики. Шарик считается годным, если отклонение Х диаметра шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая, что случайная величина Х распределена нормально со средним квадратическим отклонением 0,4 мм, найти, сколько в среднем будет годных шариков среди ста изготовленных.

8. Случайная величина Х распределена по нормальному закону с математическим ожиданием, равным 10. Вероятность попадания в интервал (10,20) равна 0,3. Чему равна вероятность попадания Х в интервал (0,10)?

9. Доказать, то Р(Х-а<t = 2Ф(t).

10. Найдите моду и медиану нормально распределенной случайной величины.

11. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 20 и 5. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (15,25).

12. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отклонением 20 г. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 10 г.

13. Деталь, изготовленная автоматом считается годной, если отклонение ее контролируемого размера от проектного не превышает 10 мм. Случайные отклонения контролируемого размера от проектного подчинены нормальному закону со средним квадратическим отклонением 5 мм и математическим ожиданием 0. Сколько процентов годных деталей изготавливает автомат?

14. Случайная величина Х распределена нормально с математическим ожиданием 25 . Вероятность попадания Х в интервал (10,15) равна 0,2. Чему равна вероятность попадания Х в интервал (35,40)?