Конспект урока по геометрии в 8б классе

18.11.10

Тема урока: «Теорема Пифагора».

Тип урока: комбинированный (изучение нового материала + первичное закрепление).

Вид урока: традиционный

Цели урока:

• Образовательные

Познакомить учащихся с теоремой Пифагора, многообразием способов ее доказательства, применением при решении задач, повторить изученный ранее материал (площадь треугольника, ромба, прямоугольника, квадрата, параллелограмма), выработать умение применять теоретический материал для решения задач и доказательства теоремы.　 Закрепить полученные знания при решении практических задач.

• Развивающие

Развивать умения обнаруживать способ доказательства нового математического утверждения и выполнять его, развивать мышление, память, навыки аргументированной речи, навыки доказательного воспроизведения в процессе деятельности.

• Воспитательные

Воспитывать настойчивость, самостоятельность в овладении математикой. Воспитывать чувство красоты эстетикой чертежей и рисунков.

Оборудование урока: доска с меловыми записями, рабочие тетради, учебник «Геометрия» 7 – 9 кл. сред. шк. / Л.С. Атанасян.

Ход урока:

I. ОНУ

Учитель: Встали ровно! Здравствуйте, садитесь. Итак, послушайте внимательно, что мы с вами будем сегодня делать. Мы с вами проверим домашнее задание и изумим новую тему. Так, Саша № 480 (б) пойдет, а Ира 479(б). А все остальные проверяем, и находим ошибки, ну если они есть.

II. Проверка домашнего задания.

Ученик: №480 (б)

Дано: АВСD – трапеция, АВ и СD – основания. = 30^о, АВ=2 см, СD = 10 см, DA = 8 см.

Найти S_АВСD.

Решение: так как = 30^о, то АН = 0,5 AD = 4 см., S_АВСD = 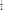(2 + 10)×4 = 24 см².

Учитель: Так проверяем у Саши, правильно?

Ученик: У меня так получилось.

Учитель: Теперь у Иры.

Ученик: №479 (б)

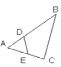
Дано:

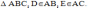
АВ = 8 см, АС = 3 см, АЕ = 2 см. S_АВС = 10 см², S_АDE = 2 см².

Найти AD.

Решение:

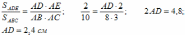
Учитель: Правильно? У кого другой ответ получился?

Ученик: Правильно. У меня так получилось.

Учитель: Хорошо садись. А теперь посмотрели все на доску и находим площадь.

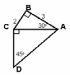
Ученик: 24, 34, 25.

Учитель: Дак сколько будет?

Ученик: 24

Учитель: Правильно. Дополнительный вопрос: какая теорема использовалась при решении задачи № 479, сформулируйте ее?

Ученик: Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

III. Изучение нового материала.

Учитель: Хорошо, а теперь сели ровненько и слушаем меня. Сегодня мы изучаем одну из самых известных геометрических теорем древности, называемую теоремой Пифагора. Ее и сейчас знают практически все, кто когда-либо изучал планиметрию. Теорема Пифагора одна из главных теорем планиметрии. Значение ее состоит в том, что с ее помощью можно доказать многие другие теоремы и решить множество задач. Знаменитый греческий философ и математик Пифагор Самосский, именем которого названа теорема, жил около 2,5 тысяч лет тому назад. Он родился в 500 г до нашей эры и прожил 80 лет. Дошедшие до нас биографические сведения о Пифагоре отрывочны и далеко не достоверны. Пифагор – это не имя, а прозвище, данное　 ему за то, что он высказывал истину так же постоянно, как дельфийский оракул «Пифагор» значит «убеждающий речью». Знаменитая теорема Пифагора звучала так: Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов построенных на его катетах. Интересная формулировка, правда?

Ученик: Да.

Учитель:

Про картинку, иллюстрирующую эту теорему, сложена шутливая поговорка: «Пифагоровы штаны на все стороны равны». Что имелось ввиду?

Ученик: Незнаем…

Учитель: Теореме Пифагора можно дать эквивалентную формулировку, применив понятие равносоставленных фигур. Попробуйте сформулировать теорему Пифагора по-другому.

Ученик: Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах.

Учитель: Чтобы сформулировать теорему Пифагора в современном изложении, давайте вспомним, как найти площадь квадрата?

Ученик: Сторону квадрата возвести в квадрат.

Учитель: Тогда площадь квадрата, построенного на гипотенузе – это …?

Ученик: Квадрат гипотенузы.

Учитель: а площади квадратов, построенных на катетах – это …?

Ученик: квадраты катетов

Учитель: Попробуйте сами дать еще одну, современную формулировку теоремы Пифагора.

Ученик: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Учитель: Давайте в своих тетрадях начертим прямоугольный треугольник, обозначим катеты и гипотенузу буквами а, b, с и запишем формулу, которую нам дает теорема Пифагора (с² = а²+b²), перед формулой запишем слово «Доказать». Сейчас известно более трёхсот доказательств теоремы Пифагора. Не подлежит, однако, сомнению, что эту теорему знали за много лет до Пифагора. Так, за 1500 лет до Пифагора древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным, и пользовались этим свойством (т.　е. теоремой, обратной теореме Пифагора) для построения прямых углов при планировке земельных участков и сооружений зданий. Это же самое проделывалось тысячи лет назад при строительстве великолепных храмов в Египте, Вавилоне, Китае. В самом древнем дошедшем до нас китайском математико-астрономическом сочинении, написанном примерно за 600 лет до Пифагора, среди других предложений, относящихся к прямоугольному треугольнику, содержится и теорема Пифагора. Еще раньше эта теорема была известна индусам. Таким образом, Пифагор не открыл это свойство прямоугольного треугольника, он, вероятно, первым сумел его обобщить и доказать, перевести тем самым из области практики в область науки. Сегодня мы с вами познакомимся с некоторыми из многочисленных доказательств теоремы Пифагора. Рассмотрим одно доказательство теоремы Пифагора, которое приведено в вашем учебнике. Оно выполнено по следующему рисунку. Вам напоминает что-нибудь этот рисунок? Когда вы это видели?

Ученик: Как в домашнем задании было.

Учитель: Достроить треугольник до квадрата со стороной (а + b) и выразить площадь квадрата возможными способами.

Перечертили еще раз этот рисунок. Доказательство (на уроке не проговаривается): S_кв. = (а + b)². С другой стороны квадрат составлен из четырех одинаковых треугольников с катетами а и в и квадрата со стороной с. Площади приравниваются: