4.2. Определение момента защемления в статически неопределимой балке.

Цель работы: Определение реактивного момента, возникающего в заделке в статически неопределимой балке и сравнение опытных данных с теоретическими.

Приборы и инструменты: Установка СМ-5, индикатор часового типа, гири 1 кг, штангенциркуль.

Краткие теоретические предпосылки.

Балки, внутренние усилия в которых не могут быть найдены из одних только уравнений равновесия статики, называются статически неопределимыми. Наиболее общим методом раскрытия статической неопределимости стержневых систем является метод сил, который заключается в том, что заданная статически неопределимая система мысленно освобождается от дополнительных связей, а их действие заменяется силами и моментами. Система, освобожденная от дополнительных связей, становится статически определимой и носит название основной системы. Для каждой статически неопределимой системы можно выбрать несколько основных систем.

Рассмотрим однопролетную балку, защемленную одним концом (рис.4.4 а). Эта балка один раз статически неопределима, поскольку неизвестных четыре (V_А, V_b, Н_А, M_А), а независимых уравнений статики можно составить три (ΣХ_і=0, ΣY_i=0, ΣМ_А=0).

На рис. 4.4б и 4.4в представлены две основных системы. Для решения задачи необходимо составить уравнение совместности деформации, выражающие ту мысль, для обеспечения эквивалентности заданной и основной системы перемещения точки В или А под действием заданной нагрузки Р и силы Х должно быт равны нулю:

Х_і_іх + Δ_ір=0.

Рис.4.4

Определение перемещения σ_іх и Δ_ір можно выполнить одним известным способом (универсальное уравнение, интеграл Мора, способ Верещагина)

Решение основной системы, представленной на рис. 4в, дает следующее значение момента защемления:

М_А = Х_і = .

После нахождения неизвестной реакции Х_і система становится статически определимой и построение эпюр изгибающих моментов и поперечных сил может быть произведено обычным способом.

Опытная установка СМ-5, на которой выполняется работа (рис. 5) представляет собой стальную балку прямоугольного сечения 1, шарнирно опертую на двух опорах (рис. 4.5). Нагружение балки может быть произведено в любой точке сосредоточенными силами (грузами) посредством подвижного подвеса 2. На левой опоре балки шарнирно закреплены рычажок 3 и грузовой рычаг 4 с подвижными грузами 5, которые поворачиваются при повороте сечения балки на опоре. Рычажок 3 служит для измерения угла поворота сечения балки с помощью индикатора 6. Поворот сечения балки вызывается сосредоточенной нагрузкой-грузами, укладываемыми на подвес 2.

После нагружения балки и взятия отсчета по индикатору, необходимо создать реактивный момент, имитирующий защемление балки на левой опоре, что достигается путем перемещения подвижного груза 5 по рычагу 4 на некоторое расстояние (плечо) - l_r. Величина плеча определяется условием возврата стрелки индикатора в начальное положение.

Порядок проведения работы:

1. Измерить длину и поперечное сечение балки.

2. Установить подвес 2 в заданной точке с координатой х = а.

3. Взять начальный отсчет по индикатору 6.

4. Нагрузить балку - положить на подвес груз в 1 кг.

5. Плавно переместить груз 5 влево (и тем самым создать защемление на левой опоре) на некоторую величину l_r, соответствующую моменту возврата стрелки индикатора в начальное 6 положение;

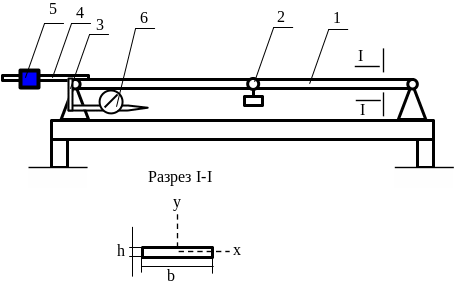
Рис 4.5.

6. Пользуясь делениями на рычаге 4, определить величину l_r, зафиксировать вес груза R.

7. Разгрузить балку.

8. Данные опыта записать в таблицу и произвести их обработку.

9. Вычислить величину реактивного момента М_А = R l_p (H·м).

10. Опыт повторить не менее 3-х раз и вычислить среднее значение М_Аср;

11. Выбрать основную систему статически неопределимой балки, соответствующую опытной установке и вычислить величину момента защемления М_Ат;

12. Произвести сравнение опытной и расчетной величин момента защемления балки

δ= ·100%

Содержание отчета.

1. Название и цель работы.

2. Теоретические предпосылки (по желанию).

3.Результаты измерений и вычислений.

4. Итоговая таблица.

5. Выводы по работе.

Контрольные вопргосы.

1. Что такое статически неопределимая система?

2. Чему равна степень статической неопределимости?

3. В чем заключается метод сил?

4. В чем отличие заданной и основной систем?

5. Запишите канонические уравнения для n статически неопределимой системы.