Составление плана действий.

Анализируя условие задачи, приходим к выводу, что нам дано численное значение q², равное 0,25, и требуется найти численное значение p². Записываем формулы закона Харди-Вайнберга и отмечаем в них информацию, полученную при анализе условия задачи. Составляемый нами план действий приобретает следующий вид.

р + q = 1

р ² + 2pq + q² = 1

Надо найти Дано

С помощью пронумерованных стрелок указываем планируемую последовательность действий при выполнении математических расчетов. Составленный нами план действий выглядит следующим образом.

2

р + q = 1

3 1

р ² + 2pq + q² = 1

Надо найти Дано

Составление наглядного плана действий существенно облегчает процесс решения задачи. Для получения ответа остается лишь выполнить несколько простых арифметических действий.

6.2. Образцы решения задач

Познакомьтесь с решением простой задачи на определение генетической структуры популяций или частоты отдельных аллелей и генотипов, при котором мы следовали предложенным рекомендациям:

• оформлять модифицированную таблицу “Признак - ген”;

• составлять наглядный план действий.

Задача 3. Анализ популяции показал, что встречаемость людей, обладающих аутосомным рецессивным признаком, равна 0,04. Какова частота гетерозигот в этой популяции?

Дано: 0,04 = q²; Необходимо найти: 2pq

Задача 8. Анализ популяции показал, что встречаемость людей, обладающих аутосомным рецессивным признаком, равна 0,04. Какова частота гетерозигот в этой популяции?

Мы решили задачу.

Теперь вспомним и повторим всю процедуру решения этой задачи.

2

р + q = 1

3 1

р² + 2рq + q² = 1

Необходимо найти Дано

___ _____

1) q = √q² = √ 0,04 = 0,2

2) р = 1 – q = 1 – 0,2 = 0,8

3) 2рq = 2 х 0,8 х 0,2 = 0,32

Ответ: частота гетерозигот в этой популяции равна 0,32.

.

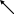
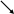
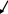
Розв’язування типових задач.

Типова задача. Встановлено, що частина особин АА в популяції зустрічається з частотою 0,09. Визначте, яка частина популяції гетерозиготна за геном А.

Методика розв’язування. Розрахунок генетичного складу популяції проводимо згідно з рівнянням Харді—Вайнберга. Частота особин АА дорівнює р2, звідси р2АА — 0,09, а р=V0,09 = 0,3. Якщо кількість гомозигот і гетерозигот виражати у відсотках, то ргАА + 2рqAa+qгаа= 100; р +q = 1; q =1-0,3= 0,7. Підставивши значення р і q у формулу, легко встановити частоту гомозигот і гетерозигот за цим геном:

р2АА = 0,32 = 0,09 = 9 %;

q2аa = 0,72 =0,49 = 49 %;

2рqАa = 2 х 0,3 х 0,7 = 0,42 = 42 %.

Отже, 42 % особин у популяції є гетерозиготами.

Розрахуємо також кількість гамет А і а, які утворюють особини в даній популяції; частота гамет А складається з 9 % гамет, які продукують особини з генотипом АА, з 21 % (42:2) гамет, що продукують гетерозиготи Аа, тобто 9 + 21 % =30 %; частота гамет а — відповідно дорівнює 49 % + 21 % = 70 %.

Типова задача. Встановлено, що популяція складається з 9/16 АА, 6/16 Аа і 1/16 аа генотипів. Чи відповідає таке співвідношення рівновазі в популяції згідно з законом Харді—Вайнберга?

Методика розв’язування. Після перетворення чисел 9/16 = 3/4 переконуємось, що популяція за даною ознакою перебуваєте стані рівноваги: (3/4)2АА : 2 х 3/4 х 1/4 Аа : (1/4)2аа. Звідси р =V9/16 = 0,75,q =V 1/16 = 0,25.

Типова задача. У сорту кукурудзи альбіносні рослини (rr) зустрічаються з частотою 0,0025. Обчисліть частоту алелів R і r, а також частоту генотипів RR і rr.

Методика розв’язування. Знаючи частоту особин з генотипом rr, тобто q2, можна_визначити частоту (q) гена в даній популяції: q =V q 2=V0,0025 = 0,05.

З формули р + q=1 знаходимо частоту (р) гена R?, а саме R =1 -0,05 = 0,95.

Типова задача. У вибірці з 84 000 рослин жита 210 рослин виявились альбіносами, тому що рецесивні гени rr знаходяться в гомозиготному стані. Визначте частоту алелів R і r, а також частоту гетерозиготних рослин — носіїв гена альбінізму.

Методика розв’язування. Визначимо частоту (q2) генотипів: rr = 210/84000 = 0,0025; частота (q) алеля r =V q2 = V0,0025 = 0,05; частота (р) алеля R= 1- q = 1 – 0,05 = 0,95; частота (2рq) гетерозиготних рослин Rr — носіїв гена альбінізму дорівнює 2 • 0,95х 0,05 = 0,095.

З

Для розв’язання задачі використовуємо формули закону Харді-Вайнберга:

р + q = 1; p² +2pq + q² = 1, де

р – частота домінантного алеля А, q – частота рецесивного алеля а, р² – частота домінантних гомозигот АА, 2рq – частота гетерозигот Аа, q² – частота рецесивних гомозигот аа.

аа = q² = √1/20000; а = q = 1/20000 = 1/141; А = р = 1– q = 1 – 1/141 = 140/141;

Аа = 2pq = 2 · 140/141·1/141 = 1/71 (0,014 або 1,4 %).

Відповідь: Один носій рецесивного гена альбінізму припадає на 71 особу.

адача 1. Альбінізм успадковується як рецесивна автосомна ознака і зустрічається з частотою 1 : 20 000. Визначте частоту гетерозигот у популяції.

Д ано:

1

аа = ――

20000

ГЕНЕТИЧНА СТРУКТУРА ПОПУЛЯЦІЇ. ЗАКОН ХАРДІ -ВАЙНБЕРГА

Під генетичною структурою популяції розуміють співвідношення особин із різними генотипами, особливості формування генетичних зв'язків (систему схрещувань) і розподіленість популяцій на ряд угрупувань (субпопуляцій), пов'язаних між собою потоками алелів. Основними параметрами генетичної структури популяцій є частоти генів і генотипів.

У популяції може існувати один, два, три чи більше (не обмежено) алелів певного гена. У конкретної диплоїдної особини з популяції -два алелі (однакових у гомозигот і різних у гетерозигот) для аутосом-них генів. Гени статевих хромосом при XY-типі визначення статі представлені одним алелем у самців і двома - у самок; при ZW-типі -навпаки (див. розділ 6).

Частота алеля визначається як відношення кількості копій даного алеля до загальної кількості алелів цього гена в усіх особин популяції. Якщо в популяції існує два алелі певного гена (скажімо, А та а), їхню частоту можна позначити як рл і qa, або просто p і q. Частота генотипу - це частка особин із певним генотипом у популяції, яку можна позначити як /(ЛА), /(Ла), /(аа).

У 1908 р. Xарді та Вайнберг (Godfrey Hardy, Wilhelm Weinberg) незалежно один від одного дійшли висновку, що за певних умов менделівсь-кий механізм спадкування забезпечує постійність (із покоління в покоління) співвідношення генотипів у популяції для будь-яких частот алелів.

Розглянемо приклад. Група із N = 200 особин має такий склад:

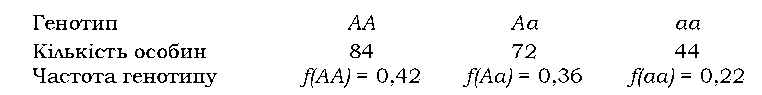
Знайдемо частоту домінантного алеля. Гомозиготи мають по два однакових алеля, гетерозиготи - лише один; загальна кількість алелів у популяції диплоїдів дорівнює подвоєній чисельності особин. Маємо

Розрахунок частот алелів дасть знову 0,6 та 0,4, і в подальших поколіннях ані ці частоти алелів, ані частоти генотипів змінюватись не будуть. Таке співвідношення генотипів у популяції, яке здатне автоматично зберігатись протягом нескінченно великої кількості поколінь, називають рівноважним співвідношенням генотипів, а явище підтримання постійного співвідношення генотипів протягом поколінь -

генетичною рівновагою. У розглянутому прикладі частоти генотипів вихідного покоління не перебували в стані рівноваги, але перейшли до рівноважного стану після першого ж панміктичного схрещування.

Отже, співвідношення генотипів у популяції буде постійним протягом нескінченної кількості поколінь для будь-яких частот алелів. Ця закономірність, відома як закон Харді - Вайнберга, описує ключову особливість популяцій - здатність до підтримання сталості частот генотипів (генетичної рівноваги). Закон Харді - Вайнберга виконується тільки для ідеальних (менделівських) популяцій: нескінченно великих панміктичних популяції диплоїдного виду зі статевим розмноженням, при однаковій життєздатності всіх генотипів і відсутності інших факторів динаміки популяції - факторів, які змінюють частоти генотипів і/або алелів (див. нижче).

Рівноважні співвідношення частот генотипів задаються піднесенням до квадрата суми частот алелів. Для двох алелів рівняння Харді -Вайнберга має такий вигляд:

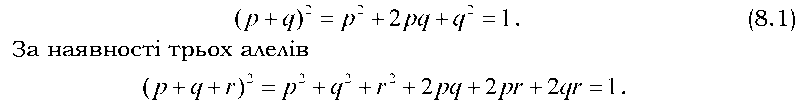
Якщо в популяції (чи в групі особин) співвідношення генотипів не рівноважне (тобто реальні співвідношення частот генотипів не відповідають теоретично очікуваним на основі закону Харді - Вайнберга для даних частот алелів), популяція перейде до стану генетичної рівноваги після першого ж панміктичного схрещування (як у розглянутому вище прикладі). Це справедливо для генів, які містяться в аутосомах.

Розглянемо встановлення генетичної рівноваги для генів, зчеплених зі статтю, зокрема з Х-хромосомою при ХY-механізмі визначення статі. У цьому випадку самки (гомогаметна стать) матимуть 2/3 всіх наявних у популяції генів (розташованих у Х-хромосомі), а самці - 1/3. У дочірньому поколінні завдяки крис-кросному механізму передачі статевих хромосом самці матимуть усі свої Х-хромосоми від матерів, а самки - одну від матері, а другу від батька. Тоді, якщо частоти алелів не однакові в самців і самок, то в кожному наступному поколінні в самців частота алеля буде дорівнювати частоті алеля самок попереднього покоління, а в самок - середньому арифметичному частот алелів самців і самок попереднього покоління. Оскільки самки мають 2/3 від усієї кількості алелів (Х-хромосом) у популяції, а самці - 1/3, то рівноважні значення частоти алелів такі:

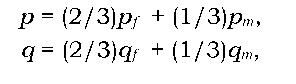
де індекс f указує на частоту (рівноважну чи нерівноважну) відповідного алеля в самок, m - у самців. У стані генетичної рівноваги частоти алелів у самок і самців однакові. Для прикладу, розглянутого на рис. 8.4, рівноважним значенням частоти алеля буде q = (2/3)qf + (1/3)qm = 2/3. Важливо розуміти, що при встановленні генетичної рівноваги за Х-зчепленими генами, частоти алелів змінюються в межах кожної статі, залишаючись постійними для популяції в цілому.

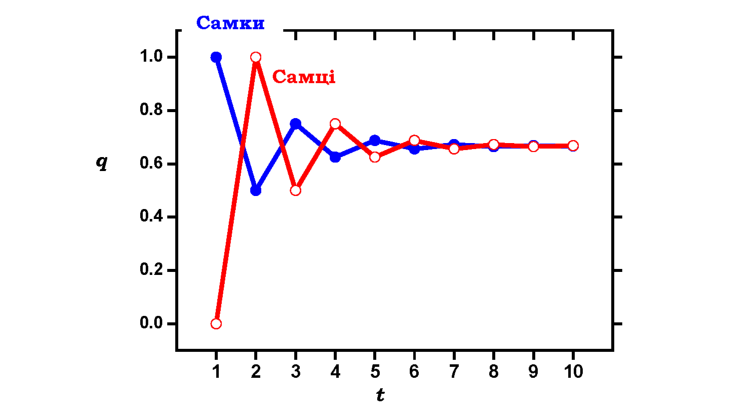
Рис. 8.4. Установлення генетичної рівноваги для Х-зчеплених генів. По осі абсцис - номер покоління t, по осі ординат - частота алеля q. Вихідні значення частоти алеля для самців qm = 0, для самок qf = 1. З кожним поколінням різниця між qm і qf зменшується, а частота алеля наближається до рівноважного значення 2/3

Перевірка рівноважності популяції проводиться шляхом порівняння (за допомогою методу %2, див. розділ 3) реального розподілу генотипів з очікуваними частотами генотипів, визначеними відповідно до закону Харді - Вайнберга. Така перевірка є можливою лише тоді, коли можна експериментально оцінити частоту гетерозигот, а саме при кодомінуванні.

За повного домінування гомозиготи АА та гетерозиготи Аа відносять до одного й того ж фенотипу, тому шляхом безпосереднього підрахунку неможливо оцінити ані частоту гетерозигот, ані частоту алелів. Це можна зробити на основі закону Харді - Вайнберга, припустивши наявність у популяції генетичної рівноваги. Зрозуміло, що в даному випадку реальні значення частот алелів можуть бути далекими від одержаних гіпотетичних.

ФАКТОРИ ДИНАМІКИ ГЕНЕТИЧНОЇ структури ПОПУЛЯЦІЙ

Нагадаємо, що умовами виконання закону Харді - Вайнберга є:

• необмеженість чисельності популяції;

• панміксія;

• відсутність мутацій;

• відсутність міграцій;

• відсутність добору.

У природі практично не буває популяцій, для яких виконувалися б усі ці умови. Якщо існують суттєві відхилення від них, то залежно від ситуації можуть змінюватись частоти генотипів при збереженні частот алелів, або ж будуть змінюватись як частоти генотипів, так і частоти алелів.

Слід, проте, зауважити, що в стаціонарних умовах середовища та для достатньо великих популяцій рівняння 8.1 виявляється справедливим для більшості генів: велика кількість генів не є об'єктами добору; для багатьох генів розподіл алелів і генотипів є подібним для різних популяцій, що змішуються між собою під час міграцій.