3. Волновое уравнение Шредингера

В квантовой механике установлено, что поведение любой частицы описывается комплексной волновой функцией ([17], гл.II, § 6). Квадрат модуля этой функции задает плотность вероятности, т.е. вероятность нахождения частицы в данном объеме пространства. Если частица движется в стационарном потенциальном поле, то волновая функция удовлетворяетволновому уравнению Шредингера

где - масса частицы,- постоянная Планка,- потенциальная энергия частицы,- полная энергия частицы.

Общее волновое уравнение Шредингера

(3)

определяет волновую функцию частицы, зависящую от координат и времени.

Для однозначного определения волновой функции задаются начальные и граничные условия и условие нормировка .

Уравнение (3) является основным уравнением квантовой механики и играет ту же роль, что уравнение Ньютона в классической механике.

§ 5. Классификация уравнений второго порядка

В предыдущих параграфах было показано, что многие важные задачи физики приводят к уравнениям в частных производных второго порядка. Дадим классификацию этих уравнений.

Рассмотрим уравнение второго порядка

, (1)

в котором коэффициенты – вещественные функции, заданные в области, причем. Зафиксируем точкуи сопоставим уравнению (1) квадратичную форму

(2)

Говорят, что уравнение (1) в точке является уравнением

- эллиптического типа, если квадратичная форма (2) положительно определенная или отрицательно определенная;

- гиперболического типа, если квадратичная форма (2) при приведении ее к каноническому виду имеет все коэффициенты, кроме одного, одного знака, а оставшийся коэффициент – противоположного знака;

- ультрагиперболического типа, если квадратичная форма (2) при приведении ее к каноническому виду имеет более одного положительного и более одного отрицательного коэффициента, причем все коэффициенты отличны от нуля;

- параболического типа, если квадратичная форма (2) при приведении ее к каноническому виду имеет только один нулевой коэффициент, а все другие коэффициенты одного знака.

Если уравнение (1) имеет один и тот же тип во всех точках области , то говорят, что оно является уравнением данного типа в области. Если все коэффициентыпостоянные, то принадлежность уравнения к тому или иному типу не зависит от значений переменных. Ясно, что уравнение Лапласа является уравнением эллиптического типа, волновое уравнение – уравнением гиперболического типа, уравнение теплопроводности – уравнением параболического типа.

Если в различных частях области уравнение (1) принадлежит различным типам, то говорят, что в областиуравнение (1) имеетсмешанный тип.

Пример. Уравнение припринадлежит эллиптическому типу, при- гиперболическому типу. Линия, разделяющая области, в которых уравнение принадлежит различным типам, называетсялинией параболического вырождения.

§ 6. Канонический вид уравнений второго порядка

Рассмотрим уравнение второго порядка с постоянными коэффициентами

, (1)

причем будем считать, что . Покажем, что (1) можно преобразовать к уравнению, в котором отсутствуют слагаемые, содержащие производные первого порядка. Введем новые переменныеравенствами

(2)

с отличным от нуля определителем . При этом

(3)

Подставив (3) в уравнение (1), получим

(4)

где. Легко видеть, что коэффициенты при вторых производных при замене независимых переменных по формулам (2) преобразуются так же, как коэффициенты квадратичной формы при аналогичном линейном преобразовании. Поэтому по закону инерции квадратичных форм ([18], гл. 6, § 27) коэффициентыв формулах (2) можно подобрать так, чтобы в уравнении (4)прии, гделибо, либо 0. При этом количество положительных, отрицательных и равных нулю коэффициентовинвариантно относительно линейного преобразования (2). Знаки коэффициентови определяют тип уравнения (1), а вид преобразованного уравнения

(5)

называется его каноническим видом.

Если все отличны от нуля, то (5) является уравнением эллиптического или гиперболического типа. В этом случае заменой функцииможно освободиться от производных первого порядка. Действительно, выполним замену

. (6)

Подставив (6) в (5), получим искомое уравнение

.

Пример 1. Привести к каноническому виду и определить тип уравнения

(7)

Решение. Уравнению (7) соответствует квадратичная форма с симметричной матрицей. Замена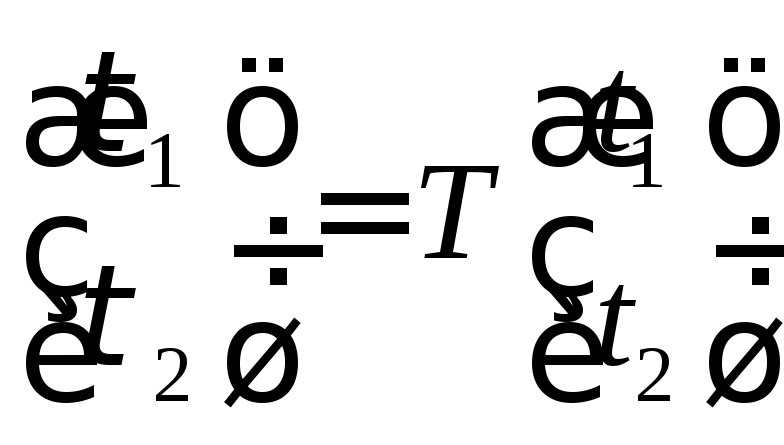, где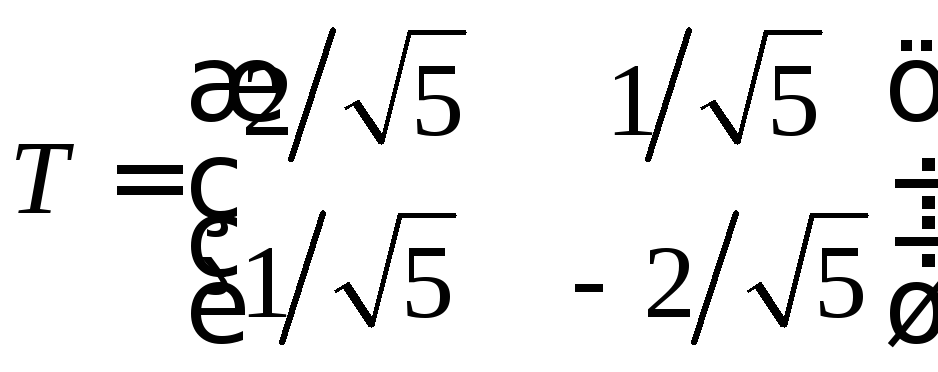- матрица, столбцами которой являются нормированные собственные векторы матрицы, отвечающие собственным числам 2 и -3 соответственно, приводит квадратичную форму к виду. Заменас матрицейприведет квадратичную форму к искомому виду. Ясно, что вместо двух последовательных преобразований было можно выполнить одно с матрицей

.

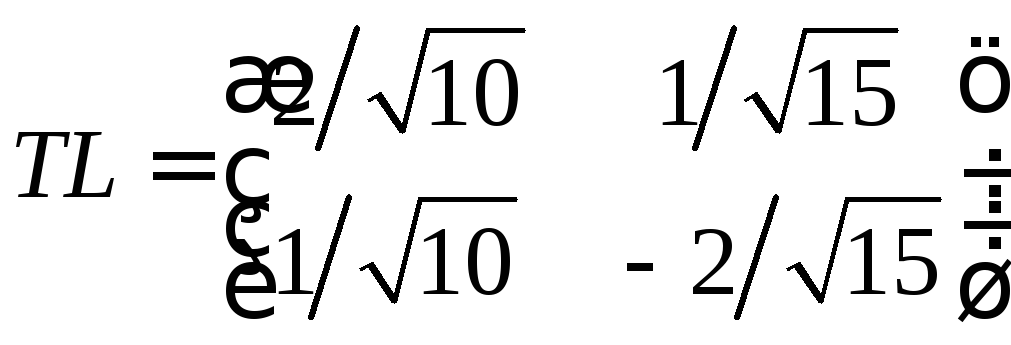В связи со сказанным выполним в (7) замену

.

После очевидных преобразований получим уравнение

,

тип которого – гиперболический.

Избавимся от слагаемых, содержащих первые производные. Для этого выполним рекомендованную замену (6):

.

Получим каноническое уравнение .

Задача 1. Привести к каноническому виду уравнения: