§ 3. Уравнения Пуассона и Лапласа

1. Стационарное уравнение теплопроводности

В предыдущем параграфе было показано, что уравнение распространения тепла в однородном изотропном теле, содержащем источники и стоки тепла, имеет вид

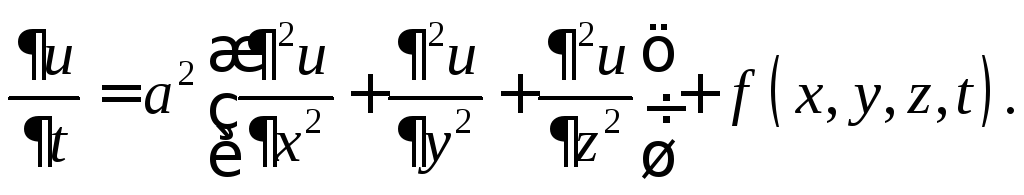
Предположим теперь, что температура в каждой точке внутри тела установилась и не меняется с течением времени. Тогда и мы приходим куравнению Пуассона

. (1)

При отсутствии источников и стоков тепла внутри тела уравнение (1) превращается в уравнение Лапласа

. (2)

Для определения функции уже не нужно задавать начальное распределение температуры (начальное условие). Достаточно задать только граничное условие.

Задача нахождения решения уравнения (1) или (2) по его значениям на границе

называется задачей Дирихле.

Если граничное условие имеет вид

,

то задача нахождения решения уравнения (1) или (2) называется задачей Неймана.

2. Стационарное уравнение мембраны

Кзадаче Дирихле сводится исследованиестационарного уравнения мембраны, натянутой на пространственный контур (рис. 6). В этом случае действующие на мембрану силы не зависят от времени, поэтому мембрана находится в состоянии покоя, а положение каждой ее точки описывается функцией, удовлетворяющей уравнению Пуассонаи граничному условию

(3)

где - проекция контурана плоскость.

Если отсутствуют силы , то положение мембраны описывается гармонической функцией, удовлетворяющей уравнению Лапласаи граничному условию (3) (такую поверхность примет мыльная пленка, натянутая на контур).

§ 4. Основные уравнения электростатики, электродинамики и квантовой механики

1. Основное уравнение электростатики

Основное свойство электростатического поля выражается следующей теоремой.

Теорема (Гаусс). Поток напряженности через произвольную замкнутую поверхностьравен, где- сумма электрических зарядов, находящихся в объеме, охваченном поверхностью:

. (1)

Если электрические заряды распределены по объему с плотностью, то равенство (1) переходит в равенство

. (2)

Для преобразования (2) воспользуемся формулой Остроградского – Гаусса (гл. I, § 2, формула (8)): . Получим равенство

Так как объем произвольный, то подынтегральное выражение должно равняться нулю тождественно, и мы получаем другую формулировку теоремы Гаусса:

Известно, что электростатическое поле потенциально: , где- скалярный потенциал поля. Поэтомуи мы получаемосновное уравнение электростатики

Это – уравнение Пуассона, если в объеме электрические заряды имеются, и уравнение Лапласа, если.

2. Основное уравнение электродинамики

Хорошо известно, что электрические заряды и токи создают в пространстве электрическое и магнитноеполя, между которыми существует сложная зависимость. Полное описание электромагнитного поля дается уравнениями Максвелла – Лоренца. В вакууме эти уравнения имеют вид

где и- плотность зарядов и токов,– скорость света. Первое уравнение означает, что источником электрического поля являются электрические заряды суммарной мощностью. Уравнениеозначает, что магнитное поле не имеет источников, т.е. является вихревым векторным полем. Уравнение, содержащее, в дифференциальной форме выражает закон электромагнитной индукции. Последнее уравнение обобщает закон Био–Савара.

Уравнения Максвелла – Лоренца показывают, что электромагнитное поле возникает не только из-за присутствия электрических зарядов, но и из-за их движения, а также из-за изменения со временем самого поля. Этим объясняется существование электромагнитного поля в пространстве, лишенном и электрических зарядов, и токов.

Если ввести векторный магнитный потенциал равенствоми скалярный электрический потенциалравенствоми использовать условие Лоренца, то уравнения Максвелла – Лоренца преобразуются в систему

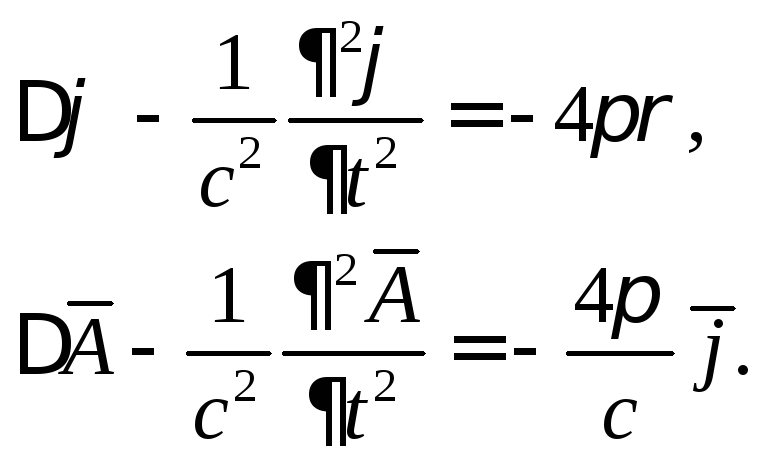
В частном случае стационарного потенциала первое из этих уравнений превращается в уравнение Пуассона. Если отсутствуют заряды, уравнение становится трехмерным волновым уравнениеми описывает волны, распространяющиеся в пространстве со скоростью света. Наконец, если поле не меняется со временем, а заряды отсутствуют, первое уравнение вырождается в уравнение Лапласа.