§ 2. Поверхностные интегралы. Основные интегральные соотношения векторного анализа

Применим идеи и методы, использовавшиеся при построении криволинейных интегралов, к построению еще одного вида интегралов - поверхностных интегралов.

Определение 1. Гладкая связная поверхность называется двусторонней поверхностью, если она не содержит замкнутой кривой, при непрерывном движении вдоль которой единичный вектор нормали к этой поверхности при возвращении в исходную точку менял бы свое направление на противоположное.

Примером поверхности, не являющейся двусторонней, является лист Мёбиуса. Его легко соорудить, склеив концы один раз перекрученной бумажной ленты.

Пусть в введена прямоугольная декартова система координати задана некоторая двусторонняя поверхностьФ. Определим на Ф как на области определения непрерывную функцию . Разобьем поверхность каким-либо способом начастей, в каждой из них возьмем произвольную точкуи построим сумму(- площадь- й части разбиения). Предел этой суммы при стремлении диаметров всех частей разбиения к нулю называетсяповерхностным интегралом первого рода и обозначается

или

При этом предполагается, что предел, если он существует, не зависит от способа разбиения поверхности Ф и от выбора точек .

Если поверхность Ф задается уравнением с непрерывно дифференцируемой поив плоской областифункцией, то, очевидно,

(1)

Формула (1) позволяет получить условия существования и свойства поверхностного интеграла первого рода. Они аналогичны свойствам криволинейных интегралов первого рода ([5], § 8, гл. V).

Если , тоесть площадь поверхностиФ.

Если интерпретировать функцию как плотность поверхностиФ в точке , то поверхностный интегралопределит массу поверхностиФ.

Задача 1. Изучить свойства поверхностного интеграла первого рода.

Задача 2. Вычислить интеграл , если:

1) Ф – часть плоскости , лежащая в первом октанте;

2) Ф – верхняя полусфера с центром в начале координат радиуса .

Задача 3. Найти массу сферы , если поверхностная плотность в точкеравна.

Перейдем к построению поверхностных интегралов другого типа. В произвольной точке двусторонней гладкой поверхностиФ проведем один из двух возможных единичных векторов нормали . Выбор этого вектора определит положительную сторону поверхностиФ и положительное направление в точке . Положительную сторону и положительное направление в произвольной точкеопределит единичный вектор нормалив этой точке, направление которого выберем так, что при непрерывном перемещении точкипо поверхности отдоединичный вектор нормалименяется также непрерывно отдо. Таким образом, будет установленаположительная сторона поверхности Ф. Другую сторону поверхности будем называть отрицательной. Отметим, что выбор положительной стороны поверхности предопределяется выбором стороны в какой-нибудь одной точке этой поверхности.

Итак, в каждой точке поверхностиФ проведем в положительном направлении единичный вектор нормали . Кроме того, предположим, что на поверхностиФ определена непрерывная вектор-функция

.

Разобьем поверхность на частей с площадямив каждой из частей отметим произвольную точкуи построим суммуили, в других обозначениях, сумму

, (2)

где - вектор, направление которого в точкесовпадает с направлением вектора, а длина равна.

Определение 2. Предел суммы (2) при стремлении диаметров всех частей разбиения к нулю, если он существует и не зависит от способа разбиения поверхности Ф и выбора точек , называетсяповерхностным интегралом второго рода и обозначается или.

Замечание. Отметим, что введенный поверхностный интеграл второго рода можно понимать как поверхностный интеграл первого рода от скалярной функции по той же поверхностиФ. Поэтому поверхностный интеграл второго рода обладает всеми свойствами поверхностного интеграла первого рода.

Поверхностный интеграл второго рода имеет следующее гидродинамическое истолкование. Каждое слагаемое в (2) задает объем цилиндра с основанием и высотой.Поэтому, если считать, что векторзадает скорость жидкости, протекающей через поверхностьФ, то определит количество жидкости, протекшей через площадкуза единицу времени в направлении вектора. Тогда поверхностный интегралопределитобщее количество жидкости, протекшей за единицу времени через поверхность Ф в положительном направлении. Благодаря такому истолкованию, поверхностный интеграл называетсяпотоком векторного поля через поверхность Ф.

Рассмотрим некоторые свойства поверхностных интегралов второго рода. Их доказательства читателю полезно получить самостоятельно или познакомиться с ними по книгам [12,13].

1. Обозначим через иположительную и отрицательную стороны поверхностиФ. Тогда

.

2. Если поверхности ине пересекаются, то

.

3. .

4. Очевидно, что

(3)

Здесь углы , образованные векторомс координатными осямисоответственно, зависят, разумеется, от точки. Так как компоненты,,векторас точностью до величин более высокого порядка малости, чем, совпадают с площадями проекцийна плоскостисоответственно, то используют также запись

5. Предположим, что двусторонняя поверхность Ф задана непрерывной функцией ,- проекцияФ на плоскость (и, следовательно, область определения функции) и вектор нормалиобразует с осьюострый угол. Тогда поверхностный интегралпреобразуется к двойному:

(4)

(Если угол тупой, тои перед двойным интегралом в (4) следует поставить знак минус).

Действительно, интегральная сумма для поверхностного интеграла есть

, (5)

где - площадь проекциина плоскость. Правая часть этого равенства является интегральной суммой для функции, определенной в области. Переходя в (5) к пределу при ранге разбиения стремящемся к нулю, получим (4).

Аналогично

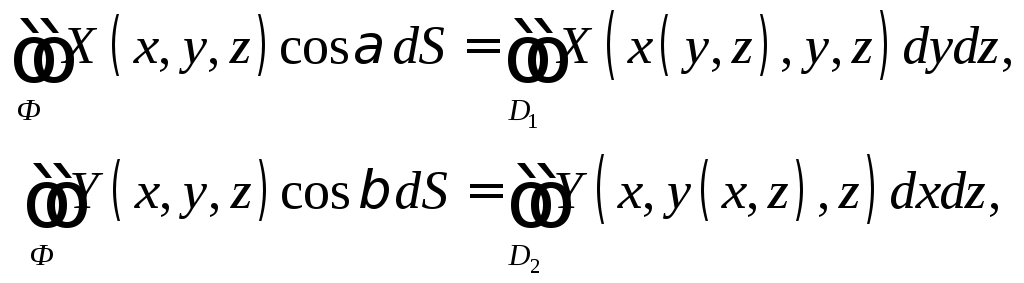(6)

где и- проекции поверхностиФ соответственно на плоскости и.

Формулы (3), (4) и (6) позволяют свести вычисление интеграла по поверхности к вычислению трех двойных интегралов.

6. Если Ф – кусочно-гладкая поверхность, ограничивающая кубируемое тело , и- вектор-функция с координатами, непрерывными вместе со всеми частными производными первого порядка в множестве, то имеет местоформула Остроградского (формула Остроградского – Гаусса)

. (7)

Используя равенство (3) и определение дивергенции векторного поля, формулу Остроградского можно записать в виде

, (8)

что позволяет определить дивергенцию по-другому, бескоординатным способом. Действительно, разделив обе части равенства (8) на объем телаи перейдя к пределу при стягивании тела в точку,, по теореме о среднем для тройных интегралов получим

. (9)

Из формулы (9) следует, что дивергенция векторного поля не зависит от системы координат, в которой задана вектор-функция . Формула (8) объясняет, почему дивергенция интерпретируется как "интенсивность" векторного поля.

7. Пусть теперь - простой замкнутый контур, являющийся краем двусторонней поверхностиФ. Тогда справедлива формула Стокса

(10)

в которой -координаты вектора- координаты внешней нормалиповерхностиФ и контур обходится в положительном направлении.

Формулу Стокса можно переписать в виде

, (11)

откуда видно, что циркуляция векторного поля вдоль края поверхности Ф равна потоку ротора этого поля через данную поверхность.

Перейдя в равенстве (11) к пределу при стягивании поверхности Ф в точку , получим бескоординатное определение ротора векторного поля:

(- площадь поверхностиФ).

Из формулы (10) следует, что при выполнении условий

(12)

криволинейный интеграл по любой пространственной кривойравен нулю. Это значит, что при выполнении условий (12) криволинейный интеграл не зависит от кривой интегрирования, а подынтегральное выражение является полным дифференциалом некоторой функции

Поэтому в этом случае имеет место аналог формулы Ньютона – Лейбница

,

где и- начало и конец дуги кривой, по которой ведется интегрирование.