4.2.5. Ввод данных пользователем

Функции ввода данных пользователем являются особо важной группой функций в пакете программ компьютерной графики, поскольку они позволяют оператору вводить команды или данные в систему. Ввод осуществляется с помощью операторских устройств ввода.

То, насколько хорошо спроектированы функции ввода данных пользователем, имеет решающее значение для обеспечения «дружественности» системы по отношению к пользователю, т. е. простоты общения с ней.

4.3. Построение геометрических фигур

4.3.1. Использование графических элементов

В системе компьютерной графики модель конструируется из графических элементов, которые запрашиваются пользователем в ходе проектирования и добавляются один к другому до получения нужной модели. Следует рассмотреть несколько аспектов такой организации процесса конструирования.

В

Рис. 4.1

о-первых, пользователь может задавать размеры, положение и ориентацию каждого нового элемента после того, как он вызван, но до момента его добавления в модель. Эти характеристики необходимы для построения модели соответствующей формы и в определенном масштабе, что реализуется путем различных преобразований, о которых упоминалось выше.

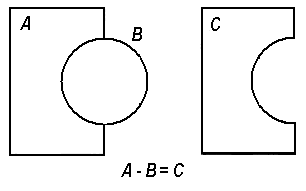
Во-вторых, над элементами графики можно производить не только действие сложения, но и вычитания, т. е. модель, может формироваться из положительных и отрицательных элементов. На рис. 4.1. иллюстрируется это свойство процесса геометрического конструирования для двумерного объекта С. Чертеж этого объекта получается путем вычитания круга В из прямоугольника А.

В-третьих, при построении геометрических моделей несколько элементов могут группироваться в блоки, которые иногда называются секциями или блоками. Термин «секция» в данном случае относится к комбинации графических элементов, которая может быть вызвана из памяти системы для использования в различных частях модели. Например, если какой-то болт многократно используется при конструировании модели механического сборочного узла, то этот графический элемент можно представить как секцию и вставлять затем в любую часть модели. Концепция графических секций является удобным и мощным средством построения геометрических моделей.

4.3.2. Определение графических элементов

В распоряжении пользователя имеется много способов вызова конкретного элемента графики и задания его местоположения в геометрической модели. Ниже дается описание ряда методов определения точек, прямых линий, дуг и других геометрических компонентов при помощи взаимодействия с интерактивной системой компьютерной графики.

4.3.2.1. Методы определения точек

1. Указание местоположения на экране с помощью органов управления курсором.

2. Ввод координат с использованием буквенно-цифровой клавиатуры.

3. Задание смещения (по координатам х, у и z) относительно ранее определенной точки.

4. Пересечение двух прямых.

5. Размещение точек на фиксированных интервалах вдоль некоторого элемента.

4.3.2.2. Методы определения линий

1. Задание двух точек.

2. Задание одной точки и угла между нужной линией и горизонталью.

3. Построение нормали или касательной к некоторой кривой в данной точке.

4. Построение линии, проходящей через некоторую точку параллельно либо перпендикулярно другой линии.

5. Построение линии, касательной к двум кривым.

6. Построение линии, касательной к кривой и параллельной либо перпендикулярной другой линии.

4.3.2.3. Методы определения дуг и окружностей

1. Задание центра и радиуса.

2. Задание центра и точки на окружности.

3. Построение кривой, проходящей через три заданные точки.

4. Построение кривой, касательной к трем линиям.

5. Задание радиуса и построение кривой, касательной к двум линиям либо кривым.

4.3.2.4. Методы определения конических сечений (эллипсов, парабол, гипербол и т. п.)

1. Задание пяти точек на данном элементе.

2. Задание трех точек и условия касания.

4.3.2.5. Методы определения кривых

Для построения кривой, проходящей через заданные точки, используются математические методы интерполяции. Например, при кубической интерполяции между каждой парой смежных исходных точек проводится полиномиальный сегмент третьего порядка. Другие применяемые в компьютерной графике способы формирования кривых основываются на использовании кривых Безье и методов В-сплайнов. И при том, и при другом подходе применяется процедура смешивания, которая обеспечивает сглаживание влияния заданных точек. Результирующая кривая при этом не обязательно проходит через все заданные точки. При использовании процедуры смешивания необходимо задавать не только точки, но еще и метод сглаживания, с помощью которого будет строиться кривая.

4.3.2.6. Методы определения поверхностей

Для математического описания поверхностей могут использоваться рассмотренные выше методы построения кривых. В автомобилестроении эти методы служат для представления рельефных поверхностей автомобильных кузовов из листового металла. К числу методов определения поверхностей относятся, например:

• задание поверхности, образуемой вращением некоторой прямой и (или) кривой вокруг заданной оси.

• задание линии пересечения двух поверхностей или плоскости, пересекающей две пересекающиеся по­верхности. Этот метод, например, можно использовать для построения поперечного разреза деталей путем рассечения данной детали плоскостью с нужной ориентацией.

Описанные выше компоненты сохраняются в базе данных в математической форме в трехмерной системе координат. Точка, например, может определяться просто своими координатами х, y и z; многоугольник обычно задается упорядоченным множеством угловых точек, а круг – центром и радиусом. Для круга на плоскости x, y можно написать уравнение:

где r – радиус окружности, а т, п – координаты ее центра. В каждом случае математическое описание можно преобразовать в соответствующие ему ребра и поверхности для занесения в базу данных и вывода на экран.