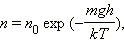- •2) Естественный способ описания движения материальной точки. Нормальное и тангенциальное ускорение. Радиус кривизны траектории.
- •3) Движение материальной точки по окружности. Угловое перемещение. Угловая скорость. Угловое ускорение. Связь между линейными угловыми величинами.
- •5) Динамика поступательного движения твердого тела. Инерциальные системы отсчета. Сила. Законы Ньютона и их современная трактовка.
- •8) Консервативные и диссипативные силы. Потенциальная энергия, работа сил(6).
- •7) Работа и мощность. Кинетическая энергия, и ее связь с работой внешних и внутренних сил.
- •10) Поле сил. Характеристики поля. Градиент потенциала.
- •9) Потенциальная энергия и ее связь с силой, действующей на систему материальных точек. Эквипотенциальные поверхности.
- •11) Кинетическая энергия поступательного и вращательного движения твердого тела. Полная механическая энергия. Закон сохранения полной механической энергии.
- •12) Момент инерции твердого тела. Свойства момента инерции. Вывод момента инерции однородного сплошного цилиндра. Теорема Штейнера-Гюйгенса.
- •16) Принцип относительности Галилея.
- •24) Идеальный газ. Уравнения состояния идеального газа. Основное уравнение молекулярно-кинетической теории идеального газа.
- •Закон взаимосвязи массы и энергии
- •21) Стационарное течение идеальной жидкости по трубе. Линии тока. Трубка тока. Уравнение неразрывности. Уравнение Бернулли.
- •22) Силы вязкого трения. Формула Ньютона для вязкости. Течение вязкой жидкости по трубам. Расход жидкости. Формула Пуазейля.
- •25) Распределение Больцмана. Распределение Максвелла. Скорости теплового движения молекул.
- •27) Адиабатический процесс. Уравнение Пуассона.
- •31) Вероятность состояния. Статистический вес состояния. Второе начало термодинамики, отражающее его статистический смысл.
- •28) Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам.
- •30) Энтропия. Второе и третье начало термодинамики. Изменение энтропии в процессах идеального газа.
- •34) Потенциальный характер электростатического поля. Потенциал. Связь между напряженностью и потенциалом. Графическое представление электрического поля. Эквипотенциальные поверхности.
- •Графическое изображение электрических полей.
- •33) Поток вектора. Теорема Остроградского-Гаусса и её применении к расчету электрических полей. Поле заряженной плоскости, двух разноименно заряженных плоскостей, заряженной сферы.
- •37) Основные уравнения электростатики диэлектриков. Электрическое смещение.
- •39) Энергия системы зарядов. Энергия и плотность энергии электрического поля.
- •40) Электрический ток, его характеристики и условия существования. Электродвижущая сила, напряжение. Закон Ома в интегральной и дифференциальной формах.
- •41) Закон Джоуля-Ленца в интегральной и дифференциальной формах. Удельная мощность тока.
- •42) Классическая электронная теория электропроводимости металлов и ее экспериментальное доказательство.
- •43) Магнитное поле и его графическое представление. Вектор магнитной индукции. Закон Био-Савара-Лапласа и его применение к расчету магнитных полей (поле прямого тока, поле кругового тока).
- •Закон Био-Савара.
- •44) Магнитный поток. Теорема Остроградского-Гаусса для магнитного поля в вакууме. Теорема о циркуляции вектора магнитной индукции, и её применении для расчета поля прямого тока, соленоида.
- •47) Гипотеза Ампера. Магнитные моменты электронов и атомов. Намагниченность. Напряженность магнитного поля.
- •48) Магнитное поле в веществе. Классификация магнетиков. Элементы теории ферромагнетизма.
- •49) Опыты Фарадея. Закон фарадея для электромагнитной индукции. Правило Ленца.
- •51) Работа по перемещению проводника и контура с током в магнитном поле.
- •52) Поведение контура с током в магнитном поле.
- •53) Энергия и плотность энергии магнитного поля.
- •55) Система уравнений Максвелла в интегральной форме. Электромагнитные волны.
- •56) Колебания. Сложение гармонических колебаний одного направления с одинаковыми частотами. Векторная диаграмма колебаний. Биения.
- •60) Вынужденные колебания в электрическом колебательном контуре (дифференциальное уравнение и его решение). Резонанс и резонансные кривые.
- •Резонанс.
- •Резонансные кривые.
25) Распределение Больцмана. Распределение Максвелла. Скорости теплового движения молекул.
Распределение Больцмана – распределение по энергиям частиц (атомов, молекул) идеального газа в условиях термодинамического равновесия было открыто в 1868–1871 гг. австрийским физиком Л. Больцманом.
В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты:
|
где n – концентрация молекул на высоте h, n0 – концентрация молекул на начальном уровне h = 0, m – масса частиц, g – ускорение свободного падения, k – постоянная Больцмана, T – температура.
Распределение Максвелла описывает распределение по скоростям молекул (частиц) макроскопической физической системы, находящейся в статическом равновесии, при условии, что движение молекул подчиняется законам классической механики (например классический идеальный газ). Установлено Дж.Максвеллом в 1859 году. Согласно распределению Максвелла, вероятное число молекул в единице объёма f(v), компоненты скоростей которых лежат в интервалах от vx до vx+dvx, vy до vy+dvy, vz до vz+dvz,
f(v) = n (m/2pkT)3/2exp( -mv2/2kT) k - постоянная Больцмана.
Молекулы газа при своем движении постоянно сталкиваются. Скорость каждой молекулы при столкновении изменяется. Она может возрастать и убывать. Однако среднеквадратичная скорость остается неизменной. Это объясняется тем, что в газе, находящемся при определенной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Скорость отдельной молекулы с течением времени может меняться, однако доля молекул со скоростями в некотором интервале скоростей остается неизменной.
Основываясь
на опыте Штерна, можно ожидать, что
наибольшее число молекул будут иметь
какую-то среднюю скорость, а доля быстрых
и медленных молекул не очень велика.
Необходимые измерения показали, что
доля молекул ![]() ,
отнесенная к интервалу скорости Δv,
т.е.
,
отнесенная к интервалу скорости Δv,
т.е. ![]() ,
имеет вид, показанный на рис. Максвелл
в 1859 г. теоретически на основании теории
вероятности определил эту функции.
,
имеет вид, показанный на рис. Максвелл
в 1859 г. теоретически на основании теории
вероятности определил эту функции.
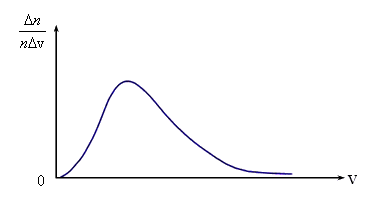
Установление этой зависимости позволило определить кроме уже известной среднеквадратичной скорости еще две характерные скорости – среднюю и наиболее вероятную. Средняя скорость – это сумма скоростей всех молекул, деленная на общее число всех молекул в единице объема.
Средняя скорость, подсчитанная на основании закона Максвелла, выражается формулой
|
|
Наиболее вероятная скорость – это скорость, вблизи которой на единичный интервал скоростей приходится наибольшее число молекул.
|
26)
Работа
газа при изменении его объёма. Внутренняя
энергия. Удельная и молярная теплоёмкости.
Формула Майера.Газ
оказывает давление на любую стенку
сосуда. Если стенка подвижна, то сила
давления F совершит
работу A,
переместив поршень на расстояние DL.
Если DL невелико,
то давление газа останется примерно
постоянным. Тогда работа будет равна:
A
= F·DL·cosa= P·S·DL, где S -
площадь поршня, a -
угол между направлением силы и перемещением
поршня (a=
0). Произведение S·DL равно
изменению объема газа DV от
начального V1 до
конечного V2значения, т.е. S·DL
=DV = V1 -
V2.
Тогда A
= P·(V2 -
V1)
= P·DV.
В изобарном процессе расширения газа P
= const.
Следовательно, при любом сколь угодно
большом увеличении объема сила давления
газа на поршень будет постоянной, и
формула работы сохранит свой вид A
= P·(V2 -V1).Теплоёмкость тела
характеризуется количеством теплоты,
необходимой для нагревания этого тела
на один градус:
![]() Размерность
теплоемкости: [C]
= Дж/К.
Однако, теплоёмкость – величина
неопределённая, поэтому пользуются
понятиями удельной и молярной теплоёмкости.
Удельная
теплоёмкость (Суд) есть
количество теплоты, необходимое для
нагревания единицы массы вещества на
1 градус [Cуд]
= Дж/К. Для газов удобно пользоваться
молярной теплоемкостью Cμ- количество
теплоты, необходимое для нагревания 1
моля газа на 1 градус:
Размерность
теплоемкости: [C]
= Дж/К.
Однако, теплоёмкость – величина
неопределённая, поэтому пользуются
понятиями удельной и молярной теплоёмкости.
Удельная
теплоёмкость (Суд) есть
количество теплоты, необходимое для
нагревания единицы массы вещества на
1 градус [Cуд]
= Дж/К. Для газов удобно пользоваться
молярной теплоемкостью Cμ- количество
теплоты, необходимое для нагревания 1
моля газа на 1 градус:![]() [Cμ] = Дж/(моль×К)молярная
масса – масса одного моля:
[Cμ] = Дж/(моль×К)молярная
масса – масса одного моля:![]() где А –
атомная масса; mед -
атомная единица массы; NА -
число Авогадро; моль μ – количество
вещества, в котором содержится число
молекул, равное числу атомов в 12 г изотопа
углерода 12С.Теплоёмкость
термодинамической системы зависит от
того, как изменяется состояние системы
при нагревании. Если газ нагревать
при постоянном
объёме,
то всё подводимое тепло идёт на нагревание
газа, то есть изменение его внутренней
энергии. Теплоёмкость при этом
обозначается СV.
СР –
теплоемкость при постоянном
давлении. Если
нагревать газ при постоянном давлении Р в
сосуде с поршнем, то поршень поднимется
на некоторую высоту h,
то есть газ совершит работу. Следовательно,
проводимое тепло затрачивается и на
нагревание и на совершение работы.
Отсюда ясно, что
где А –
атомная масса; mед -
атомная единица массы; NА -
число Авогадро; моль μ – количество
вещества, в котором содержится число
молекул, равное числу атомов в 12 г изотопа
углерода 12С.Теплоёмкость
термодинамической системы зависит от
того, как изменяется состояние системы
при нагревании. Если газ нагревать
при постоянном
объёме,
то всё подводимое тепло идёт на нагревание
газа, то есть изменение его внутренней
энергии. Теплоёмкость при этом
обозначается СV.
СР –
теплоемкость при постоянном
давлении. Если
нагревать газ при постоянном давлении Р в
сосуде с поршнем, то поршень поднимется
на некоторую высоту h,
то есть газ совершит работу. Следовательно,
проводимое тепло затрачивается и на
нагревание и на совершение работы.
Отсюда ясно, что
![]() Итак,
проводимое тепло и теплоёмкость зависят
от того, каким путём осуществляется
передача тепла. Значит, Q и С
не являются функциями состояния.
Величины СР и СV оказываются
связанными простыми соотношениями.
Найдём их.Пусть мы нагреваем один моль
идеального газа при постоянном объёме(dA =
0). Тогда первое начало термодинамики
запишем в виде:
Итак,
проводимое тепло и теплоёмкость зависят
от того, каким путём осуществляется
передача тепла. Значит, Q и С
не являются функциями состояния.
Величины СР и СV оказываются
связанными простыми соотношениями.
Найдём их.Пусть мы нагреваем один моль
идеального газа при постоянном объёме(dA =
0). Тогда первое начало термодинамики
запишем в виде:
![]() т.е.
бесконечно малое приращение количества
теплоты
т.е.
бесконечно малое приращение количества
теплоты ![]() равно
приращению внутренней энергии dU.
Теплоемкость
при постоянном объёме будет
равна:
равно
приращению внутренней энергии dU.
Теплоемкость
при постоянном объёме будет
равна:![]() (4,2,4)В
общем случае
(4,2,4)В
общем случае
![]() так
как U может
зависеть не только от температуры.
Из (4.2.4) следует, что
так
как U может
зависеть не только от температуры.
Из (4.2.4) следует, что ![]() ,
,
![]()
![]() (4,2,5)Внутренняя
энергия идеального газа является только
функцией температуры (и
не зависит от V, Р и тому подобных), поэтому
формула (4.2.5) справедлива для любого
процесса.
Для произвольной идеальной массы газа:
(4,2,5)Внутренняя
энергия идеального газа является только
функцией температуры (и
не зависит от V, Р и тому подобных), поэтому
формула (4.2.5) справедлива для любого
процесса.
Для произвольной идеальной массы газа:![]() При изобарическом процессе, кроме
увеличения внутренней энергии, происходит
совершение работы газом:
При изобарическом процессе, кроме
увеличения внутренней энергии, происходит
совершение работы газом:
![]()
![]() Из
основного уравнения молекулярно-кинетической
теории
Из
основного уравнения молекулярно-кинетической
теории ![]() .
При изобарическом процессе Р = const.
Следовательно, из (4.2.7) получим:
.
При изобарическом процессе Р = const.
Следовательно, из (4.2.7) получим:![]() -
Это уравнение
Майера для
одного моля газа.
Из этого следует, что физический
смысл универсальной газовой постоянной
в том, что R – численно равна работе,
совершаемой одним молем газа при
нагревании на один градус в
изобарическом процессе. формула
Майера для удельных теплоёмкостей:
-
Это уравнение
Майера для
одного моля газа.
Из этого следует, что физический
смысл универсальной газовой постоянной
в том, что R – численно равна работе,
совершаемой одним молем газа при
нагревании на один градус в
изобарическом процессе. формула
Майера для удельных теплоёмкостей:![]() или
или
![]()