
- •2) Естественный способ описания движения материальной точки. Нормальное и тангенциальное ускорение. Радиус кривизны траектории.
- •3) Движение материальной точки по окружности. Угловое перемещение. Угловая скорость. Угловое ускорение. Связь между линейными угловыми величинами.
- •5) Динамика поступательного движения твердого тела. Инерциальные системы отсчета. Сила. Законы Ньютона и их современная трактовка.
- •8) Консервативные и диссипативные силы. Потенциальная энергия, работа сил(6).
- •7) Работа и мощность. Кинетическая энергия, и ее связь с работой внешних и внутренних сил.
- •10) Поле сил. Характеристики поля. Градиент потенциала.
- •9) Потенциальная энергия и ее связь с силой, действующей на систему материальных точек. Эквипотенциальные поверхности.
- •11) Кинетическая энергия поступательного и вращательного движения твердого тела. Полная механическая энергия. Закон сохранения полной механической энергии.
- •12) Момент инерции твердого тела. Свойства момента инерции. Вывод момента инерции однородного сплошного цилиндра. Теорема Штейнера-Гюйгенса.
- •16) Принцип относительности Галилея.
- •24) Идеальный газ. Уравнения состояния идеального газа. Основное уравнение молекулярно-кинетической теории идеального газа.
- •Закон взаимосвязи массы и энергии
- •21) Стационарное течение идеальной жидкости по трубе. Линии тока. Трубка тока. Уравнение неразрывности. Уравнение Бернулли.
- •22) Силы вязкого трения. Формула Ньютона для вязкости. Течение вязкой жидкости по трубам. Расход жидкости. Формула Пуазейля.
- •25) Распределение Больцмана. Распределение Максвелла. Скорости теплового движения молекул.
- •27) Адиабатический процесс. Уравнение Пуассона.
- •31) Вероятность состояния. Статистический вес состояния. Второе начало термодинамики, отражающее его статистический смысл.
- •28) Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам.
- •30) Энтропия. Второе и третье начало термодинамики. Изменение энтропии в процессах идеального газа.
- •34) Потенциальный характер электростатического поля. Потенциал. Связь между напряженностью и потенциалом. Графическое представление электрического поля. Эквипотенциальные поверхности.
- •Графическое изображение электрических полей.
- •33) Поток вектора. Теорема Остроградского-Гаусса и её применении к расчету электрических полей. Поле заряженной плоскости, двух разноименно заряженных плоскостей, заряженной сферы.
- •37) Основные уравнения электростатики диэлектриков. Электрическое смещение.
- •39) Энергия системы зарядов. Энергия и плотность энергии электрического поля.
- •40) Электрический ток, его характеристики и условия существования. Электродвижущая сила, напряжение. Закон Ома в интегральной и дифференциальной формах.
- •41) Закон Джоуля-Ленца в интегральной и дифференциальной формах. Удельная мощность тока.
- •42) Классическая электронная теория электропроводимости металлов и ее экспериментальное доказательство.
- •43) Магнитное поле и его графическое представление. Вектор магнитной индукции. Закон Био-Савара-Лапласа и его применение к расчету магнитных полей (поле прямого тока, поле кругового тока).
- •Закон Био-Савара.
- •44) Магнитный поток. Теорема Остроградского-Гаусса для магнитного поля в вакууме. Теорема о циркуляции вектора магнитной индукции, и её применении для расчета поля прямого тока, соленоида.
- •47) Гипотеза Ампера. Магнитные моменты электронов и атомов. Намагниченность. Напряженность магнитного поля.
- •48) Магнитное поле в веществе. Классификация магнетиков. Элементы теории ферромагнетизма.
- •49) Опыты Фарадея. Закон фарадея для электромагнитной индукции. Правило Ленца.
- •51) Работа по перемещению проводника и контура с током в магнитном поле.
- •52) Поведение контура с током в магнитном поле.
- •53) Энергия и плотность энергии магнитного поля.
- •55) Система уравнений Максвелла в интегральной форме. Электромагнитные волны.
- •56) Колебания. Сложение гармонических колебаний одного направления с одинаковыми частотами. Векторная диаграмма колебаний. Биения.
- •60) Вынужденные колебания в электрическом колебательном контуре (дифференциальное уравнение и его решение). Резонанс и резонансные кривые.
- •Резонанс.
- •Резонансные кривые.
21) Стационарное течение идеальной жидкости по трубе. Линии тока. Трубка тока. Уравнение неразрывности. Уравнение Бернулли.
Идеальной жидкостью назвается воображаемая несжимаемая жидкость, в которой отсутствуют вязкость, внутреннее трение и теплопроводность. Так как в ней отсуствует внутреннее трение, то нет касательных напряжений между двумя соседними слоями жидкости.
Для графического изображения течения жидкости часто используют линии тока – линии, касательная к которым в каждой точке совпадает с вектором скорости частицы. При этом линии тока рисуют так, чтобы густота линий тока (число линий, пронизывающих площадку единичной площади в перпендикулярном им направлении) была пропорциональна величине вектора скорости. В случае стационарного течения картина линий тока не изменяется, а сами они совпадают с траекториями движения молекул жидкости. Поверхность, образованная линиями тока, проведенными через все точки замкнутого контура, называется трубкой тока. При стационарном течении жидкости ее молекулы не пересекают трубку тока.
При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии. Следствием этого закона для стационарного потока идеальной и несжимаемой жидкости является уравнение Бернулли (1738 г.). Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока. Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости. Рассмотрим течение идеальной жидкости внутри некоторой трубки тока, обладающей такими сечениями, что скорость молекул жидкости в любой точке каждого из них одинакова. Так как идеальная жидкость несжимаема, то ее масса, сосредоточенная между сечениями S1 и S2 трубки тока, с течением времени не изменяется. Поэтому объемы жидкости dQ, протекшие через эти сечения за промежуток времени dt, будут равны. Поскольку dQ = S·v·dt, то выполняется соотношение:S·v = const. Это выражение называется уравнением неразрывности. Его физический смысл заключается в том, что жидкость нигде не накапливается, т. е. за одинаковый временной интервал в трубку тока втекает и вытекает равные количества жидкости.
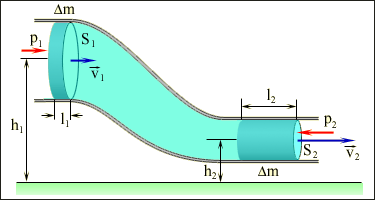
Уравнение Бернулли — для стабильно текущего потока (газа или жидкости) сумма кинетической и потенциальной энергии, давления на единицу объема является постоянной в любой точке этого потока.
![]()
Первое и второе слагаемое в Законе Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. А третье слагаемое в нашей формула является работой сил давления и не запасает какую-либо энергию. Из этого можно сделать вывод, что размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости или газа.
Постоянная в правой части уравнения Бернулли называется полным давлением и зависит в общих случаях, только от линии потока.
22) Силы вязкого трения. Формула Ньютона для вязкости. Течение вязкой жидкости по трубам. Расход жидкости. Формула Пуазейля.
Трение – один из видов взаимодействия тел. Оно возникает при соприкосновении двух тел. Трение, как и все другие виды взаимодействия, подчиняется третьему закону Ньютона: если на одно из тел действует сила трения, то такая же по модулю, но направленная в противоположную сторону сила действует и на второе тело. Силы трения, как и упругие силы, имеют электромагнитную природу. Они возникают вследствие взаимодействия между атомами и молекулами соприкасающихся тел.
Силами сухого трения называют силы, возникающие при соприкосновении двух твердых тел при отсутствии между ними жидкой или газообразной прослойки. Они всегда направлены по касательной к соприкасающимся поверхностям.
При движении твердого тела в жидкости или газе возникает силa вязкого трения. Сила вязкого трения значительно меньше силы сухого трения. Она также направлена в сторону, противоположную относительной скорости тела. При вязком трении нет трения покоя.
При достаточно малых скоростях величина силы вязкого трения пропорциональна скорости относительного движения υ тел, пропорциональна площади S и обратно пропорциональна расстоянию между плоскостями h.
Коэффициент пропорциональности, зависящий от сорта жидкости или газа, называют коэффициентом динамической вязкости.
Сила вязкого трения сильно зависит от скорости тела. При малых скоростях Fтр ~ υ, при больших скоростях Fтр ~ υ2. При этом коэффициенты пропорциональности в этих соотношениях зависят от формы тела.
Основной закон
вязкого течения был
установлен И. Ньютоном (1687) для тонкого
слоя жидкости (газа), зажатого между
пластинами, движущимися параллельно
с разными скоростями v1 и v2. Вектора
скорости по всему слою жидкости
(газа) направлены параллельно, модуль
скорости линейно зависит от поперечной
координаты (Рис. 1). Закон утверждает,
что на пластины будет действовать сила,
величина которой определяется
формулой:![]() Здесь F –
касательная к поверхности пластин сила,
вектор которой совпадает по направлению
с векторами v1 и v2, S –
площадь слоя, по которому происходит
сдвиг; z -
поперечная толщина слоя. Коэффициент
пропорциональности
Здесь F –
касательная к поверхности пластин сила,
вектор которой совпадает по направлению
с векторами v1 и v2, S –
площадь слоя, по которому происходит
сдвиг; z -
поперечная толщина слоя. Коэффициент
пропорциональности ![]() называется коэффициентом
динамической вязкости или
просто вязкостью. Он характеризует
сопротивление жидкости (газа) смещению
ее слоёв. Кинематической
вязкостью
называется коэффициентом
динамической вязкости или
просто вязкостью. Он характеризует
сопротивление жидкости (газа) смещению
ее слоёв. Кинематической
вязкостью ![]() называется
отношение динамической вязкости к
плотности жидкости (газа).
называется
отношение динамической вязкости к
плотности жидкости (газа).
В системе СИ единица динамической вязкости – Па*с (паскаль-секунда), в СГС – пуаз (пз) (1 пз = 10-1 Па*с), единица измерения кинематической вязкости в СИ - м2/с, в СГС - стокс (Ст), 1 Ст = 10-4 м2/с.
Течение жидкости по трубе. Формула Пуазейля.
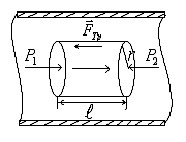 Пологая
течение жидкости ламинарным, найдём
закон изменения скорости v с расстоянием
r от оси трубы, т.е. v(r) -? Выделим воображаемый
цилиндрический объём жидкости радиуса
r и длинны l. Поскольку скорости всех
частиц жидкости являются постоянными
v = const, сумма внешних сил, приложенных к
любому объёму жидкости, равна нулю. На
основание цилиндра действуют силы
давления, сумма которых равна:
Пологая
течение жидкости ламинарным, найдём
закон изменения скорости v с расстоянием
r от оси трубы, т.е. v(r) -? Выделим воображаемый
цилиндрический объём жидкости радиуса
r и длинны l. Поскольку скорости всех
частиц жидкости являются постоянными
v = const, сумма внешних сил, приложенных к
любому объёму жидкости, равна нулю. На
основание цилиндра действуют силы
давления, сумма которых равна: ![]() .
На боковую поверхность цилиндра действует
сила трения:
.
На боковую поверхность цилиндра действует
сила трения: ![]() .
Поскольку
.
Поскольку ![]() ,
то
,
то ![]() .
.
Учитывая,
что скорость убывает с расстоянием от
оси трубы, т.е. ![]() ,
из (1) получим:
,
из (1) получим: ![]() ,
, ![]() Интегрирование
даёт:
Интегрирование
даёт: ![]() Так как при r = R скорость v = 0, то
Так как при r = R скорость v = 0, то ![]() ,
где R – радиус трубы.
,
где R – радиус трубы.
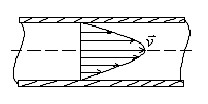
![]() -
закон изменения скорости жидкости от
расстояния до оси трубы. Если
-
закон изменения скорости жидкости от
расстояния до оси трубы. Если ![]() -
скорость на оси трубы, то
-
скорость на оси трубы, то ![]()
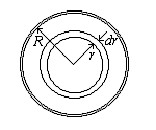 Вычислим
поток жидкости Q – т. е. объём жидкости,
протекающей через поперечное сечение
трубы за единицу времени. Для этого
сначала определим поток жидкости через
кольцо радиуса r и толщиной dr :
Вычислим
поток жидкости Q – т. е. объём жидкости,
протекающей через поперечное сечение
трубы за единицу времени. Для этого
сначала определим поток жидкости через
кольцо радиуса r и толщиной dr :![]() -поток
жидкости через кольцо dr. Интегрируя по
r, получим поток жидкости через поперечное
сечение трубы.
-поток
жидкости через кольцо dr. Интегрируя по
r, получим поток жидкости через поперечное
сечение трубы.
![]() -формула
Пуазейля .
-формула
Пуазейля .
29)Цикл Карно и его КПД.
Машина Карно — это тепловая машина, работающая между двумя резервуарами с температурами T1 и Т2 (Т1 > T2) по обратимому циклу, состоящему из двух изотерм и двух адиабат (циклу Карно).
Если машина работает между двумя резервуарами 1 и 2), причем в ходе процесса тепло отбирается у резервуара 1, а отдается резервуару 2, то произведенная работа оказывается равной А = Q1_получ - Q2_отд, а для КПД получается формула
эта = 1 - Q2/Q1.
23) Виды течений. Число Рейнольдса. Критерии подобия. Формула Стокса.
Число,
или, правильнее, критерий
Рейно́льдса (![]() ), —
безразмерная величина, характеризующая
отношение нелинейного и диссипативного
членов в уравнении
Навье — Стокса[1].
Число Рейнольдса также считается критерием
подобия течения
вязкой жидкости.Число
Рейнольдса определяется следующим
соотношением:
), —
безразмерная величина, характеризующая
отношение нелинейного и диссипативного
членов в уравнении
Навье — Стокса[1].
Число Рейнольдса также считается критерием
подобия течения
вязкой жидкости.Число
Рейнольдса определяется следующим
соотношением:
![]()
![]() — плотность среды,
кг/м3;
— плотность среды,
кг/м3;![]() —
характерная скорость,
м/с.
—
характерная скорость,
м/с.![]() — гидравлический
диаметр,
м;
— гидравлический
диаметр,
м;
— динамическая
вязкость среды,
Н·с/м2![]() — кинематическая
вязкость среды,
м2/с
(
— кинематическая
вязкость среды,
м2/с
(![]() );
);![]() —
объёмная скорость потока;
—
объёмная скорость потока;
![]() —
площадь
сечения трубы.
—
площадь
сечения трубы.
Рассмотрим условия, которые должны быть выполнены для динамического подобия потоков жидкости. Движение жидкости в природе совершается под действием различных сил, которые можно приближенно классифицировать на три группы:
1) внешние силы по отношению к жидкости, например, силы тяжести, инерции, силы, обусловленные перепадом давления;
2) силы, связанные с физическими свойствами самой жидкости, такие, как силы вязкости или силы поверхностного натяжения;
3) результирующие силы типа силы сопротивления воды движению тела или силы воздействия жидкости на гидротехническое сооружение.
Каждая из этих сил выражается через физические величины (размерные коэффициенты), характеризующие природу сил и жидкости. Влияние указанных сил проявляется в неодинаковой степени в различных явлениях. Одни явления протекают под преобладающим действием сил тяжести и сопротивления, другие – сил тяжести, со противления и поверхностного натяжения или только сил тяжести и поверхностного натяжения и т.д.УсловияГидродинамического подобия модели и натуры требуют равенства на модели и в натуре отношений всех сил, под действием которых протекает явление.Для установления условий (критериев) гидродинамического подобия необходимо рассмотреть дифференциальные уравнения движения, описывающие изучаемое явление. Предполагая, что два потока, обтекающие тело, будут гидродинамически подобны, эти потоки должны принадлежать к одному классу уравнений, т.е. описываться однотипными уравнениями.
Движение вязкой несжимаемой жидкости, которое мы будем рассматривать, записывается системой дифференциальных уравнений Навье – Стокса [85]
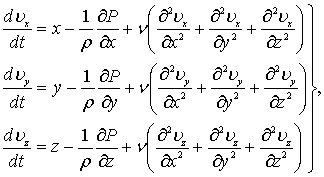 (8.7)
(8.7)
где X, Y, Z – проекции вектора напряжения массовых сил на оси координат.Эти уравнения являются математическим выражением равновесия внешних сил, приложенных к жидкости (например, сил тяжести), сил инерции, сил давления и сил внутреннего трения (сил вязкости).
Левые части уравнений (8.7) представляют собой проекции полных ускорений, которые в развернутом виде определяются следующими выражениями:
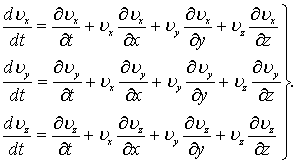 (8.8)
(8.8)
На основе анализа уравнений Навье – Стокса, записанных в форме (8.8), получим основные критерии подобия вязкой несжимаемой жидкости. Поскольку два подобных явления различаются между собой только лишь постоянными множителями для каждой одноименной величины (константами подобия), можно перейти от уравнений справедливых для натурного потока, к уравнениям, относящимся к модельному потоку, умножая каждую величину, входящую в уравнение (8.8) на соответсвующую константу подобия.
