34) Потенциальный характер электростатического поля. Потенциал. Связь между напряженностью и потенциалом. Графическое представление электрического поля. Эквипотенциальные поверхности.

Взаимодействие между неподвижными электрическими зарядами осуществляется посредствомэлектростатического поля. Оно действует на электрические заряды (заряженные тела и частицы), вносимые в это поле  с силой, которая не зависит от скорости движения заряда.

Напряженность, потенциал, разность потенциалов электростатического поля. Электрическое поле характеризуется в каждой точке напряженностью   и потенциалом φ: ,        .

Напряженность электрического поля – силовая характеристика электрического поля, она численно равна силе действующей на единичный положительный электрический заряд, помещенный в данную точку поля. Потенциалом электрического поля называется физическая величина, равная отношению потенциальной энергии пробного точечного заряда, помещенного в данную точку поля, к величине этого заряда. Потенциал – энергетическая характеристика электрического поля, определяется через понятие энергии или работы. Приведём ещё одно определение потенциала электрического поля. Потенциалом электрического поля в данной точке называется величина, численно равная работе, совершаемой при перемещении единичного положительного заряда из данной точки поля С на бесконечность  . Знак потенциала зависит от знака заряда, который создает электрическое поле. Разность потенциалов   – физическая величина, численно равная работе, совершаемой при перемещении единичного положительного заряда из точки поля 1 в точку 2:  . Размерности [Е] и [φ] в СИ  соответственно   (вольт на метр) и  (вольт). Соотношения между напряженностью и потенциалом электрического поля:  , где   – разность потенциалов на расстоянии  . Знак минус означает, что направление вектора    противоположно направлению роста потенциала. Проекция вектора напряженности электростатического поля на произвольное направление численно равна быстроте убывания потенциала поля на единицу длины в этом направлении. В общем случае   и соотношение между напряженностью и потенциалом имеет вид:  .

Графическое изображение электрических полей.

Электрические поля можно изображать графически: при помощи силовых линий или эквипотенциальных поверхностей (которые взаимно перпендикулярны между собой в каждой точке поля. Силовыми линиями (линиями напряженности) называются линии, касательные в каждой точке к которым совпадают с направлением вектора напряженности в данной точке. Эквипотенциальные поверхности – это поверхности равного потенциала.

33) Поток вектора. Теорема Остроградского-Гаусса и её применении к расчету электрических полей. Поле заряженной плоскости, двух разноименно заряженных плоскостей, заряженной сферы.

если силовые линии однородного электрического поля напряженностью пронизывают некоторую площадку S, то поток вектора напряженности (число силовых линий через площадку) будет определяться формулой

где E_n – произведение вектора на нормаль к данной площадке (рисунок 2.5).

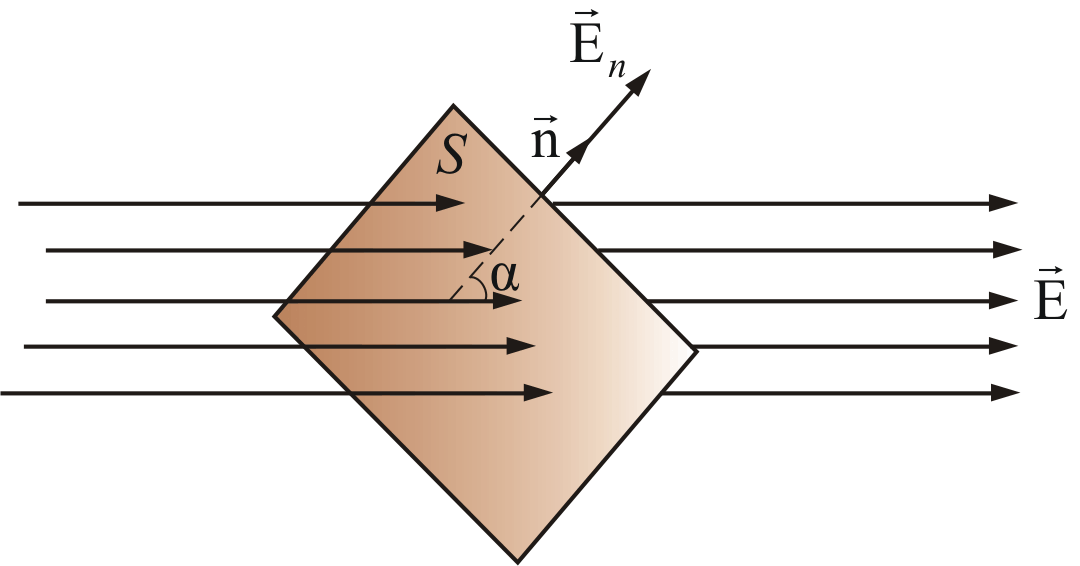
Рисунок 2.5

Полное число силовых линий, проходящих через поверхность S, называется потоком вектора напряженности Ф_Е через эту поверхность. Элементарный поток вектора напряженности через площадку dS определится соотношением: , где – проекция на направление нормали . В векторной форме можно записать – скалярное произведение двух векторов, где вектор . Таким образом, поток вектора есть скаляр, который в зависимости от величины угла α может быть как положительным, так и отрицательным. Полный поток вектора напряженности через любую площадку S можно определить тогда , а поток через замкнутую поверхность, окружающую заряд или заряженное тело равен .

Теорема Остроградского-Гаусса:

Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.

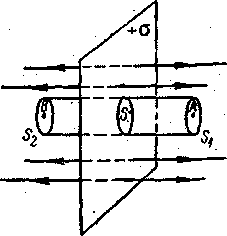
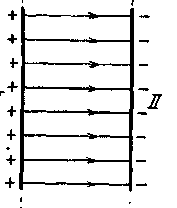
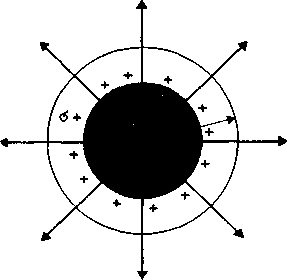
 Напряженность поля равномерно заряженной бесконечной плоскости. Пусть электрическое поле создается бесконечной плоскостью, заряженной равномерно с поверхностной плотностью заряда +σ =d q/dS (рисунок - 3.8,а). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (cos α = 0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания E совпадает с E_n), т.е. равен 2ES. Заряд, заключенный внутри построенной цилиндрической поверхности, равен σS. Согласно теореме Остроградского — Гаусса, 2ES = σS/ε₀, откуда E = σ/(2ε₀). Из формулы следует, что E не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно. ^ Поле двух бесконечных параллельных разноименно заряженных плоскостей (рисунок - 3.8,б). Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями +σ и -σ Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля Е = 0. В области между плоскостями Е = Е⁺ + Е^- (Е⁺ и Е^- напряженности от соответствующих знакам зарядов плоскостей. Поэтому результирующая напряженность Е= σ/ε₀. Таким образом, результирующая напряженность поля между плоскостями описывается полученной формулой, а вне объема, ограниченного плоскостями, равна нулю. ^ Поле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R с общим зарядом q заряжена равномерно с поверхностной плотностью +σ (рисунок - 3.8,в). Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально. 

а)	б)	в)
Рисунок - 3.8

Построим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если r>R, то внутрь поверхности попадает весь заряд q, создающий рассматриваемое поле, и, по теореме Остроградского-Гаусса, 4πr²E = q/ε₀, откуда E = q/4πr²ε₀ (r›R). При r‹R поле убывает с расстоянием по такому же закону, как у точечного заряда. Если r<R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (Е = 0).

36) Сегнетоэлектрики и их свойства.

Сегнетоэлектриками называют полярные диэлектрики, которые в определенном интервале температур спонтанно (самопроизвольно) поляризованы, т. е.обладают поляризованностью при отсутствии внешнего электрического поля. К сегнетоэлектрикам относятся сегнетова соль NaKC4H4O6×4Н2О, титанат бария ВаTiО3, триглицинсульфат (NH2CH2COOH3)3×3H2SO4. В настоящее время известно уже свыше ста сегнетоэлектриков.

Сегнетоэлектрики обладают рядом своеобразных электрических свойств:

1. Диэлектрическая проницаемость e сегнетоэлектриков очень велика (103¸104), в то время как у большинства обычных диэлектриков она составляет несколько единиц.

2. Диэлектрическая проницаемость e сегнетоэлектриков является функцией напряженности   внешнего электрического поля и температуры.

3. У сегнетоэлектриков температурная зависимость e имеет один или несколько выраженных максимумов (рис. 8). Температуры, при которых наблюдаются эти максимумы называются точками Кюри (Тк). Сегнетова соль имеет две точки Кюри (+22,5°С и –15°С). При нагревании сегнетоэлектрика выше Тк он утрачивает необыкновенные свойства и становится обычным диэлектриком. У сегнетоэлектриков, которые имеют две и больше точек Кюри, особые свойства наблюдаются только при температурах, лежащих в пределах между этими точками. Зависимость e от температуры подчиняется закону Кюри-Вейсса:

где b – константа, равная приблизительно 10-5¸10-6 град-1.

5. Для сегнетоэлектриков характерно явление насыщения, состоящее в том, что начиная с некоторого значения Е, Р не изменяется.

35) Проводники и диэлектрики. Типы диэлектриков. Поляризация диэлектриков. Поляризованность.

При равновесии объемная плотность электричества внутри однородного проводника равна нулю. Электричество располагается на его поверхности. Напряжённость поля вблизи поверхности проводника E=4pi sigma n (из граничных условий, при E1=0). Сила на ед.площади f = sigma/2 * E = 2pi sigma^2 n = E^2/8pi n.

Диэлектриками называются вещества, которые в обычных условиях практически не проводят электрический ток, их удельное сопротивление в  раз больше, чем у металлов. Согласно представлениям классической физики, в диэлектриках, в отличие от проводников, нет свободных носителей заряда, которые могли бы под действием электрического поля создавать ток проводимости.

В диэлектриках, как и в металлах, могут возбуждаться

индукционные заряды. Заряды могут смещаться из своих положений равновесия лишь на малые расстояния, порядка атомных. Под действием поля центр тяжести электронов в молекулах смещается относительно центра тяжести атомных ядер. Молекулы становятся эл. диполями, положительные концы диполей ориентированы по E. Это явление — эл. поляризация. На границе появляются нескомпенсированные индукционные заряды — поляризационные (связанные). Кроме нейтральных молекул, могут присутствовать ионы — свободные заряды. Молекулы, у которых есть дипольный момент в отсутствие поля — полярные.

а) Неполярные диэлектрики

В диэлектрическом поле на положительные и отрицательные заряды молекул будут действовать равные и противоположные силы, растягивающие молекулу (рис. 5.2.). Действие этих сил приводит к деформации молекул и к возникновению у них дипольного момента:  . Величина этого момента, как показывает опыт, пропорциональна напряжённости поля  , поэтому такие молекулы называют ещё упругими диполями.

б) Полярные диэлектрики

Полярные молекулы не меняют величину своего дипольного момента под действием электрического поля. В отличие от неполярных молекул, они ведут себя как жёсткие диполи.

В электрическом поле на такую жесткую молекулу действует вращающий момент, стремящийся ориентировать дипольные моменты молекул вдоль поля

в) Ионные диэлектрики

В электрическом поле положительные и отрицательные подрешётки ионной структуры смещаются друг относительно друга, и при этом возникает дипольный момент.

Все эти явления, происходящие в диэлектриках в присутствии электрического поля, называются поляризацией. В первом случае это была деформационная поляризация, во втором — ориентационная, в третьем — ионная.

Если поместить диэлектрик во внешнее электрическое поле, то он поляризуется, т. е. получит неравный нулю дипольный момент p_V=∑p_i где p_i — дипольный момент одной молекулы. Чтобы произвести количественное описание поляризации диэлектрика вводят векторную величину — поляризованность, которая определяется как дипольный момент единицы объема диэлектрика: