4.2. Задача нелінійного програмування

Лінійні моделі є ефективним засобом дослідження широкого кола задач управління та економіки. Виникнення НП пов’язане з тим, що припущення про лінійну залежність можуть лише наближено характеризувати об’єкт дослідження. В більшості випадків залежність між основними параметрами системи є нелінійною.

Наприклад, дохід від реалізації продукції є нелінійною функцією ціни: чим нижча ціна тим більший попит і, відповідно, більший обсяг реалізації. Закон спадаючої ефективності виробництва свідчить про нелінійну залежність обсягів виробництва від собівартості продукції. Різного виду затрати праці та матеріальних ресурсів, як правило, є нелінійними функціями точності, надійності та інших характеристик якості продукції виробництва.

В зв’язку з вищесказаним, виникає потреба у використанні нелінійних моделей як більш узгоджених з практикою.

НП охоплює широкий клас настільки складних задач, що досі не розроблені загальні методи, подібні СМ в ЛП, які б дозволяли розв’язувати будь-які ЗНП. Проблеми розв’язування нелінійних задач на відміну від ЗЛП, полягають перш за все в тому, що область допустимих розв’язків в них може бути неопуклою або мати нескінченне число кутових точок, або і перше і друге одночасно. При нелінійності цільової функції виникають і інші труднощі: оптимум може досягатися не тільки на границі, але і в середині допустимої області; цільова функція може мати в допустимій області декілька локальних екстремумів.

В загальному вигляді ЗНП формулюється так: знайти вектор , який задовольняє системі обмежень

(4.13)

і забезпечує екстремум функції _{. (4.14)}

При цьому вважають, що функції і відомі. Як і для ЗЛП, на всі або частину змінних задачі накладаються умови невід’ємності._. Крім цього, обмеженням може бути умова цілочисельності розв’язку для деяких або всіх змінних.

Якщо , , ,де – відомі сталі, то при умові невід’ємності розв’язків отримаємо ЗЛП.

В залежності від виду системи обмежень і цільової функції ЗНП діляться на задачі:

– дробово-лінійного програмування (ДЛП) – коли цільова функція раціональна, а система обмежень задається системою лінійних рівнянь і нерівностей;

– опуклого програмування – коли цільова функція та обмеження відповідно опуклі функції та опуклі області;

– квадратичного програмування – коли цільова функція квадратична, обмеження є системою лінійних рівнянь і нерівностей.

4.3. Дробово-лінійне програмування

Як було зазначено вище, нелінійність задачі МП визначається нелінійністю цільової функції, або нелінійністю системи обмежень або і тим і другим. Задачі НП, в яких цільова функція є раціональною, а система обмежень — лінiйна, складають основу ДЛП. Вони шляхом нескладних перетворень зводяться до ЗЛП.

Розглянемо наступну задачу ДЛП: знайти екстремум функції

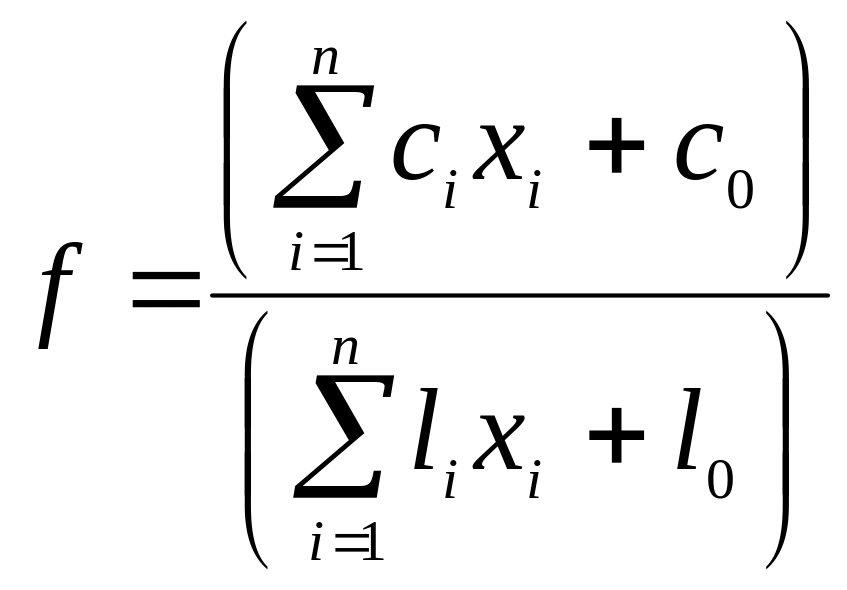(4.15)

при обмеженнях

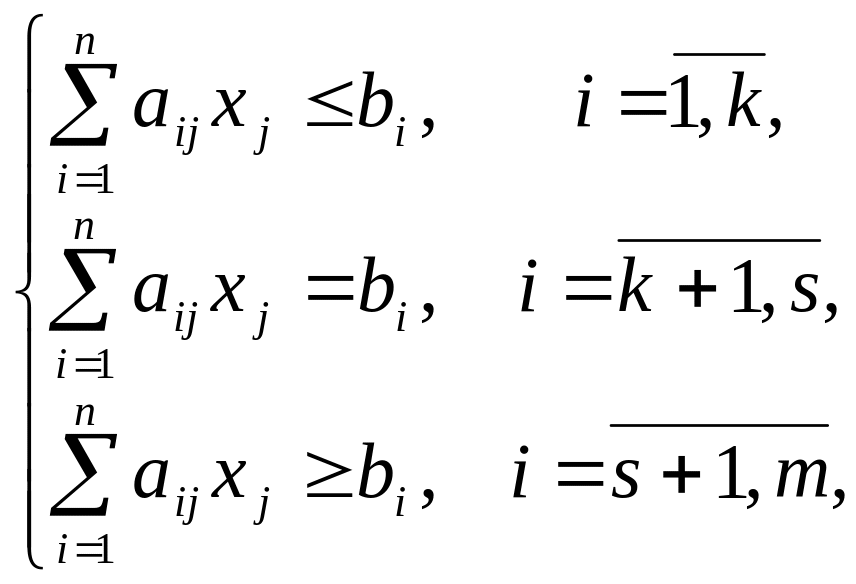
(4.16)

Розглянемо лише випадок, коли на допустимій множині планів задачі . Якщо , то задача (4.15)–(4.16) не має оптимального розв'язку, оскільки цільова функція необмежена на множині допустимих розв'язків.

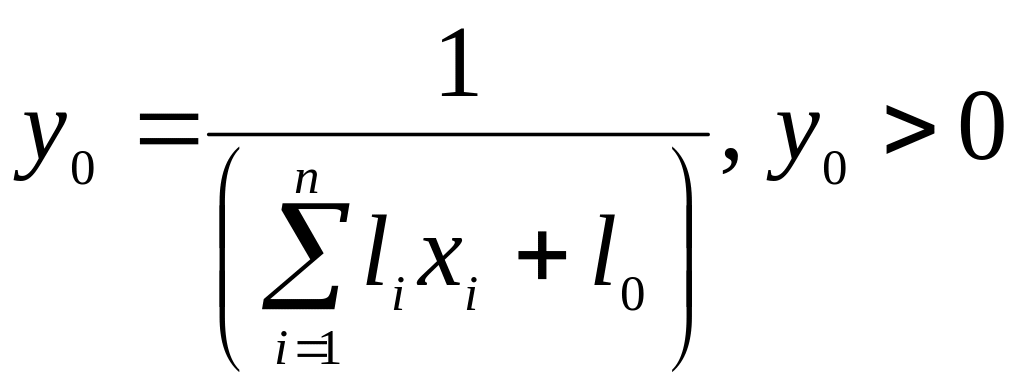
Позначивши , задачу (4.15) — (4.16) запишемо у вигляді: знайти найбільше значення функції

(4.17)

при обмеженнях

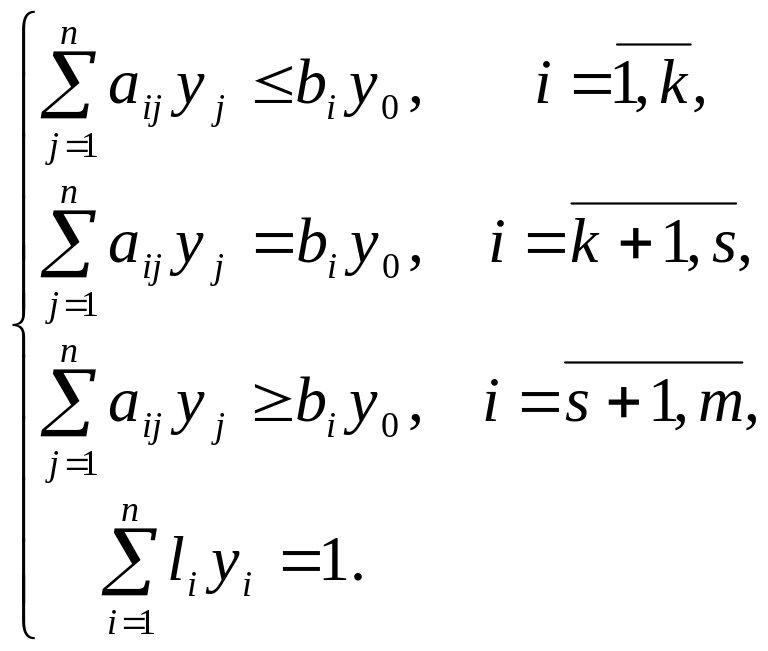(4.18)

(4.19)

Задача (4.17) – (4.19) є ЗЛП, яку ми можемо розв'язати СМ. Знайшовши її оптимальний розв'язок, , випишемо оптимальний розв'язок задачі (4.15) – (4.16) , де і .

Приклад 4.5. Знайти найбільше значення функції 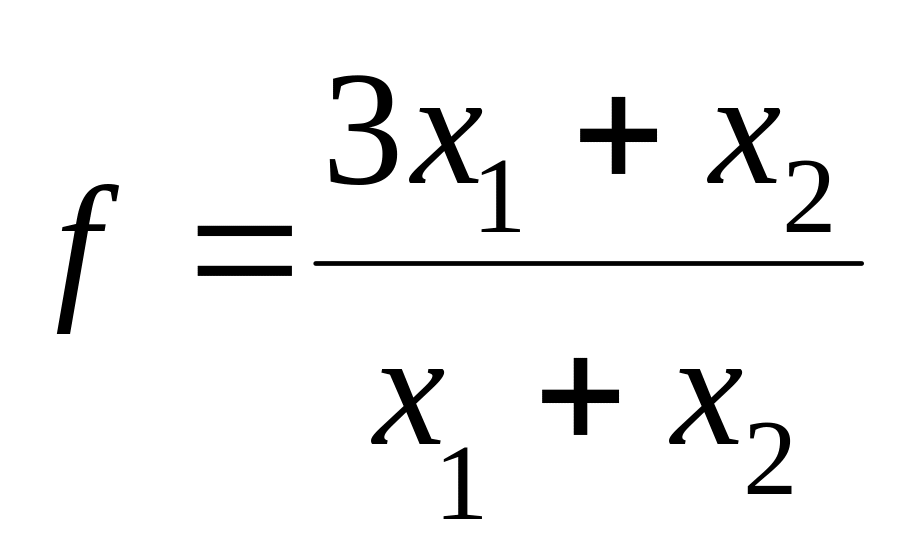при обмеженнях

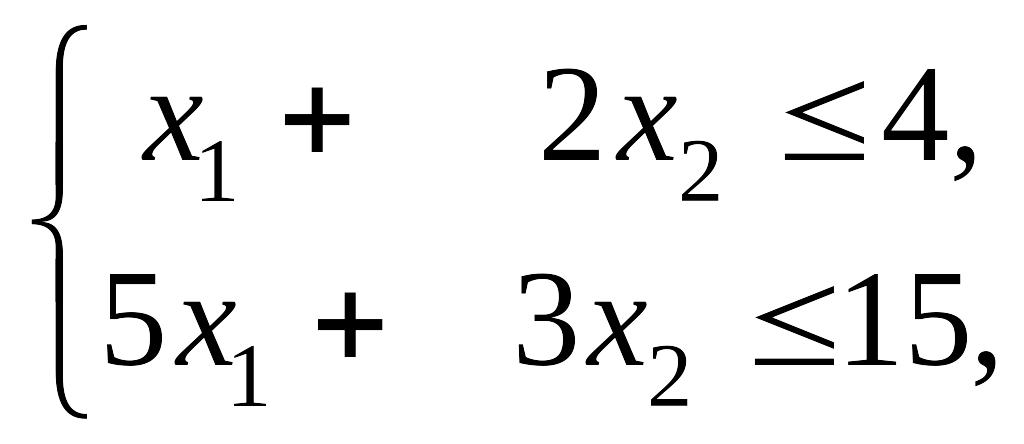
Розв'язок. Виходячи зі змісту задачі, змінні і не можуть бути одночасно рівними нулю, а це означає, що величина додатна. Позначивши , початкову задачу перепишемо так: знайти найбільше значення функції при обмеженнях

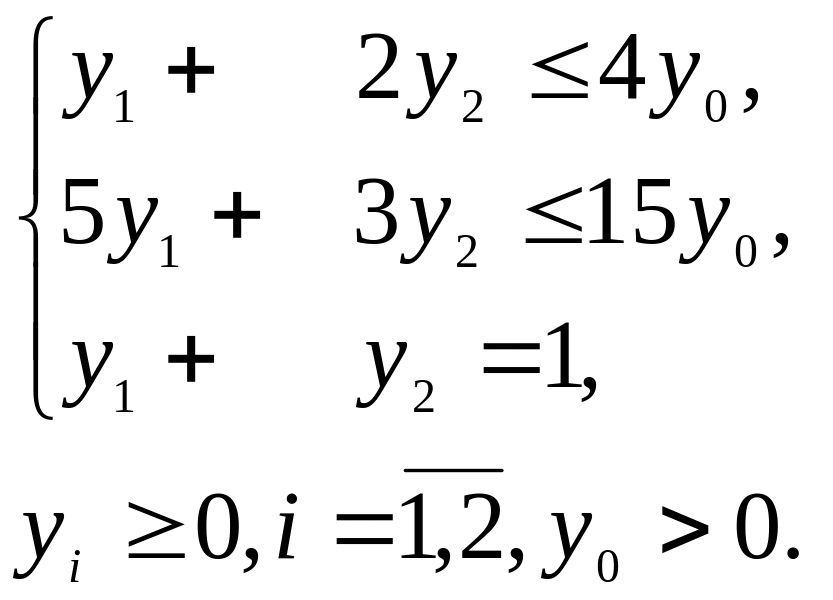
Запишемо задачу в канонічній формі: знайти найбільше значення функції при обмеженнях

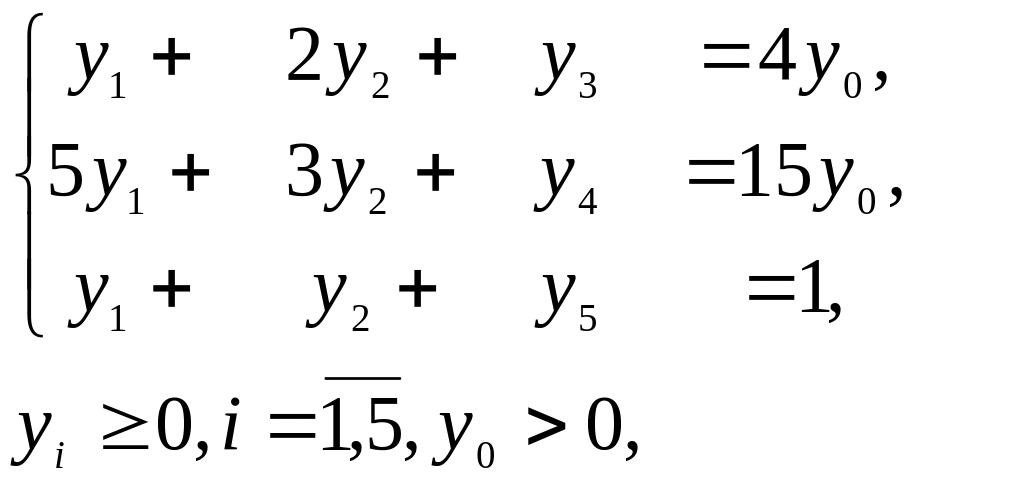
і запишемо у вигляді, зручному для запису у симплексну таблицю:

Тоді перша симплексна таблиця буде мати вигляд:

				1
	–4	1	2	0
	–15	5	3	0
0	0	1	1	1
	0	–3	–1	0

Реалізуючи послідовно алгоритм СМ для ЗЛП, записаних в загальному вигляді, отримаємо

				1							1
	–4	1	2	0				4/5	–15/5	–18/5	0
	5	–5	–7	0				1/5	–1	–7/5	0
0	4	–1	–1	1			0	–4/5	15/5	23/5	1
	–12	3	5	0				12/5	–45/5	–59/5	0

		0		1						1
	0	1	1	1				0	1	1
	–5/25	5/15	0	5/15				–5/25	0	5/15
	–4/5	5/15	23/5	5/15				–4/5	23/5	5/15
	0	3	36/5	3				0	36/5	3

3 останньої симплексної таблиці виписуємо оптимальний розв'язок: і Тоді розв'язок поставленої задачі:

, , і .