Приклад 3.3. Виконати всі можливі спрощення платіжної матриці

.

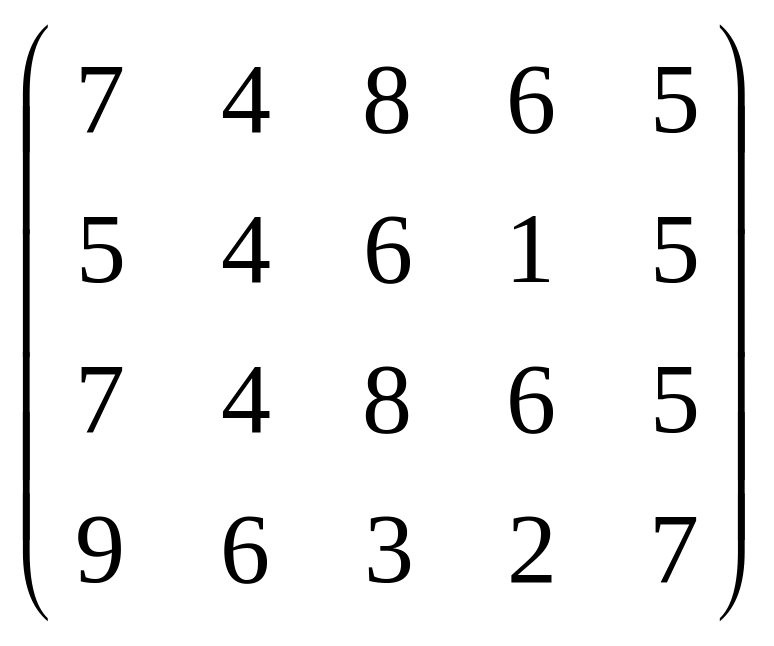Розв’язок. Користуючись зауваженнями 3.1 і 3.2, отримаємо

Наступна теорема широко використовується при спрощенні платіжних матриць.

Теорема 3.4. Нехай P^* і Q^*– оптимальні змішані стратегії гравців A і B в грі I з матрицею (a_ij)_{m n} і ціною . Тоді P^*і Q^* будуть оптимальними і в грі I^ з матрицею (ba_ij+c)_{m n} (b>0) і ціною

Приклад 3.4. Спростити платіжну матрицю

.

Розв’язок. Розділивши елементи матриці на 100 і додавши до одержаних значень 3, отримаємо .

3.4. Числові методи розв’язування матричних ігор

Розглянемо випадок, коли в матриці гри (a_ij)_m×n всі a_ij>0. Ясно, що тоді і ціна гри . Знайдемо спочатку оптимальну змішану стратегію Q=(q₁;...;q_n) гравця B. Застосовуючи її, гравець B програє не більше від при будь-якій чистій стратегії A_i гравця A, тобто

Розділивши обидві частини останньої нерівності на , дістанемо , звідки, позначивши отримаємо

(3.8)

Крім того, задовольняє умові Гравець B намагатиметься зробити свій гарантований програш якомога меншим, а значить, якомога більшою величину

Таким чином, приходимо до наступної задачі: знайти найбільше значення функції

(3.9)

при обмеженнях (3.8).

Це типова ЗЛП, записана в симетричній формі. Розв'язавши її, знайдемо оптимальний вектор і , а потім, використовуючи, що , , визначимо ціну гри і компоненти оптимальної змішаної стратегії Q^*:

(3.10)

Міркуючи аналогічно, приходимо до задачі: знайти найменше значення функціїї

(3.11)

при обмеженнях

(3.12)

розв'язуючи яку, знайдемо оптимальний вектор і .

Далі,

(3.13)

а оптимальна змішана стратегія гравця A буде

Задачі (3.8)–(3.9) і (3.11)–(3.12) утворюють пару двоїстих задач ЛП, а тому розв'язавши одну з них (наприклад, (3.8)–(3.9)), зразу можемо виписати розв'язки другої. Проілюструємо це на прикладі.

Приклад 3.4. Знайти розв'язок гри з матрицею

Розв'язок. Знайдемо спочатку оптимальну змішану стратегію гравця B. Для цього запишемо задачу (3.8)–(3.9): знайти найбільше значення функції при обмеженнях

Ввівши змінні зведемо її до канонічної форми.

Розв’язуючи задачу СМ, приходимо до таблиці 3.5.

Таблиця 3. 5

Оптимальний розв'язок За формулою (3.10) знаходимо ціну гри і Отже,

Задача для визначення компонент вектора , а отже, і компонент оптимальної змішаної стратегії P^* гравця A в канонічній формі має вигляд: мінімізувати функцію при обмеженнях

Тут базисними є змінні x₄, x₅, і x₆, а вільними – x₁, x₂, x₃. Враховуючи відповідності між змінними розглядуваної пари Д3, з таблиці 3.5 знайдемо За формулою (3.13) одержимо Таким чином, – оптимальна змішана стратегія гравця A.

При розв’язуванні матричних ігор розміром 2  n і m  2 доцільніше використовувати графічний метод і властивості оптимальних розв'язків пари ДЗ: якщо в оптимальному розв'язку задачі змінна додатна, то обмеження ДЗ, яке відповідає цій змінній, перетворюється в рівність. Якщо оптимальним розв'язком задачі обмеження перетворюється в строгу нерівність, то в оптимальному розв'язку ДЗ відповідна змінна рівна 0.

Приклад 3.5. Знайти розв'язок гри з матрицею

Розв'язок. Врахувавши відношення домінування рядків і стовпців і додавши до всіх елементів матриці число 5, отримаємо:

Для визначення оптимальних стратегій гравців складаємо пару ДЗ. Для гравця A знайти найменше значення при обмеженнях

(3.14)

для гравця B: знайти найбільше значення функції при обмеженнях

(3.15)

Розв'язуючи задачу (3.14) графічним методом, знаходимо Оскільки то обидва обмеження в (3.15) її оптимальним розв'язком перетворюються в рівності. Крім того, при перші два обмеження (3.14) перетворюються в строгі нерівності. Отже, відповідні змінні y₁ і y₂ в оптимальному розв'язку (3.15) дорівнюють нулю (значить, . Для знаходження і залишається розв'язати систему рівнянь . Звідки а отже , Крім того, Тоді, , а ціна гри