
- •Розділ 3. Елементи теорії ігор
- •3.1. Предмет і деякі основні поняття теорії ігор
- •3.2. Матричні ігри. Розв’язування матричних ігор в чистих стратегіях
- •3.3. Розв’язування матричних ігор в змішаних стратегіях
- •Приклад 3.3. Виконати всі можливі спрощення платіжної матриці
- •Приклад 3.4. Спростити платіжну матрицю
- •3.4. Числові методи розв’язування матричних ігор
- •3.5. Елементи теорії статистичних ігор
- •Контрольні запитання та задачі
- •Які ситуації називаються конфліктними?
- •Розділ 4. Нелінійне програмування (нп)
- •4.1. Відомості з теорії функцій багатьох змінних
- •4.1.1. Функція. Частинні похідні. Диференціал
- •4.1.2. Екстремум функції багатьох змінних
- •4.2. Задача нелінійного програмування
- •4.3. Дробово-лінійне програмування
- •4.4. Метод множників Лагранжа. Економічний зміст множників Лагранжа
- •4.5. Графічний метод розв'язування задач нп
- •4.6. Теорема Куна-Таккера
- •Контрольні запитання та задачі
- •5.1. Основні поняття дп
- •5.2. Постановка задач дп. Метод функціональних рівнянь р.Белмана
- •5.3. Економічні задачі, що розв'язуються методом дп
- •5.3.1. Задача розподілу ресурсів
- •5.3.2. Задача про збільшення виробничих потужностей за рахунок відрахувань з прибутку
- •5.3.3. Задача про вибір найбільш економного маршруту постачання вантажу
- •5.3.4. Задача мінімізації витрат пального літаком при набиранні висоти і швидкості
- •5.3.5. Задача заміни обладнання
- •5.4. Детерміновані та стохастичні задачі дп
- •Контрольні запитання та задачі
- •Розділ 6. Елементи стохастичного програмування
- •6.1. Загальна характеристика задач стохастичного програмування
- •6.2. Задача розподілу ресурсів в стохастичному варіанті
- •6.3 Задача про агента
- •Контрольні запитання та задачі
- •Розділ 7. Використання Пакетів прикладних програм при розв’язуванні злп
- •7.1. Загальні зауваження
- •7.2. Розв’язування задач математичного програмування за допомогою ms excel
- •7.2.1. Розв’язування злп записаних в стандартному вигляді
- •Ввести умову задачі:
- •Розв’язати задачу:
- •Послідовність виконання операцій
- •Ввід початкових даних.
- •7.2.2. Розв’язування зцлп
- •Після натискання кнопки Выполнить отримуємо:
- •У кінцевому звіті маємо: .
- •7.2.3.Транспортна задача
- •7.3. Використання пакету Maple для розв’язування задач лінійного програмування
- •Зразки контрольних робіт та індивідуальні завдання
- •Контрольна робота №1
- •Критерій оцінювання
- •Контрольна робота №2
- •Критерій оцінювання
- •Індивідуальні завдання Індивідуальне завдання 1
- •Індивідуальне завдання 2
- •Індивідуальне завдання 3
- •Індивідуальне завдання 4
- •Індивідуальне завдання 5
- •Індивідуальне завдання 6
- •Індивідуальне завдання 7
- •Індивідуальне завдання 8
- •Індивідуальне завдання 9
7.2.2. Розв’язування зцлп
Реалізацію алгоритму отримання цілочислового розв'язку ЗЛП проілюструємо на прикладі 1.13 з параграфу 1.6.3:
Приклад 7.2.
Знайти найбільше значення функції
![]() при обмеженнях
при обмеженнях
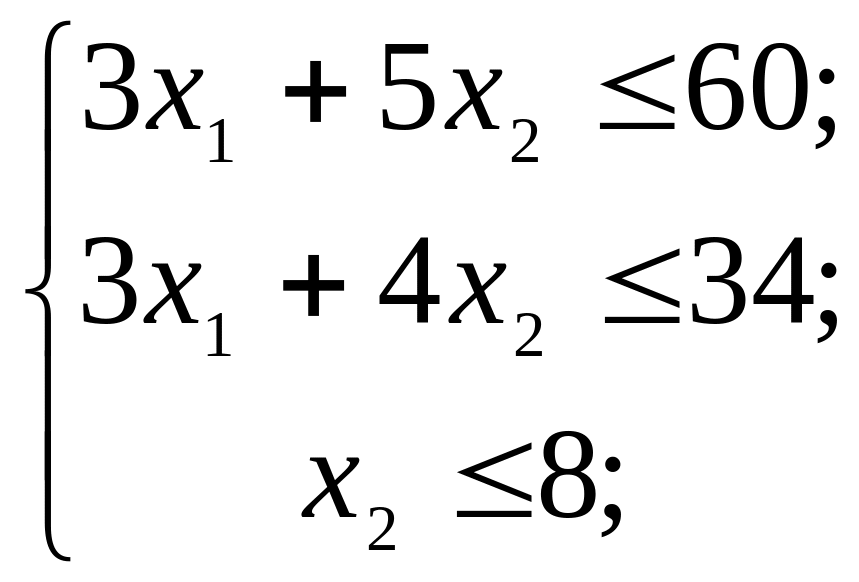
![]() ;
;
![]() ,
,
![]() ,
,
![]() -
цілі числа.
-
цілі числа.
Спочатку знайдемо нецілочисловий розв'язок задачі. Для цього представимо задачу в наступному екранному вигляді:
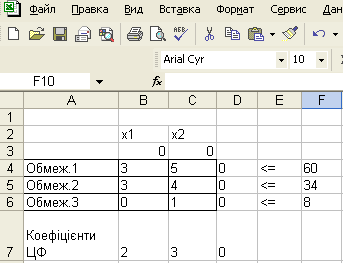
Рис.7.13. Таблиця для введення початкових даних
Далі виконуємо команду Сервис/Поиск решения.
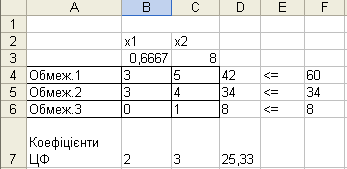
Рис.7.14. Результат розв’язування ЗЛП
Оскільки, розв'язок
![]() не цілочисловий, то для отримання
цілочислового розв'язку додається
додаткова умова цілочисельності змінних.
Для цього:
не цілочисловий, то для отримання
цілочислового розв'язку додається
додаткова умова цілочисельності змінних.
Для цього:
в екранній формі потрібно вказати, на які змінні накладаються умови цілочисельності;
в вікні Сервис/Поиск решения натисніть кнопку ДОБАВИТЬ і у вікні, що з’явилося ДОБАВИТЬ ОГРАНИЧЕНИЯ введіть обмеження так:
в полі ССЫЛКА НА ЯЧЕЙКУ введіть адреси комірок змінних задачі $В$3:$С$3;
в поле вводу знаку обмеження встановіть ЦЕЛОЕ;
підтвердіть ввід обмеження натисканням кнопки ОК.
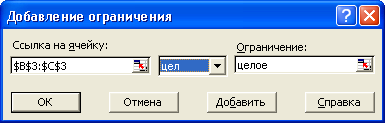
Рис.7.15. Діалогове вікно Add Constraints
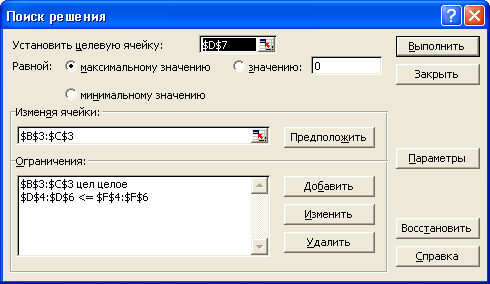
Рис.7.16. Діалогове вікно Solver Parameters
Після натискання кнопки Выполнить отримуємо:
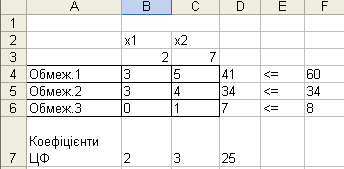
Рис.7.17. Результат розв’язування ЗЦЛП
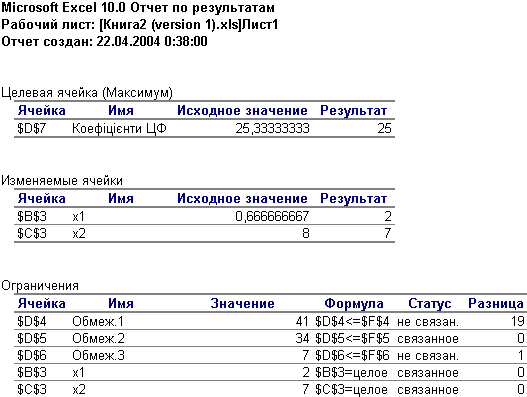
Рис.7.18. Звіт за результатами
У кінцевому звіті маємо: .
7.2.3.Транспортна задача
Приклад 7.3. В чотирьох сховищах
А![]() ,
А
,
А![]() ,
А
,
А![]() ,
А
,
А![]() є в наявності 40; 50; 60; 30 т палива. Потрібно
спланувати перевезення палива трьом
споживачам В
,
В
,
В
,
попит яких відповідно рівний 60; 80; 40 т
так, щоб витрати на транспортування
були мінімальними. Вартість перевезень
1 т вказана в табл.2.
є в наявності 40; 50; 60; 30 т палива. Потрібно
спланувати перевезення палива трьом
споживачам В
,
В
,
В
,
попит яких відповідно рівний 60; 80; 40 т
так, щоб витрати на транспортування
були мінімальними. Вартість перевезень
1 т вказана в табл.2.
Таблиця 2
-
Сховище
Вартість перевезення 1 т палива
споживачам, грн.
Запаси палива,т
В
В
В
А
4
3
5
40
А
6
2
1
50
А
7
4
2
60
А
5
6
3
30
Потреба в паливі, т
60
80
40
Розв’язування. Запишемо задачу в екранній формі наступним чином
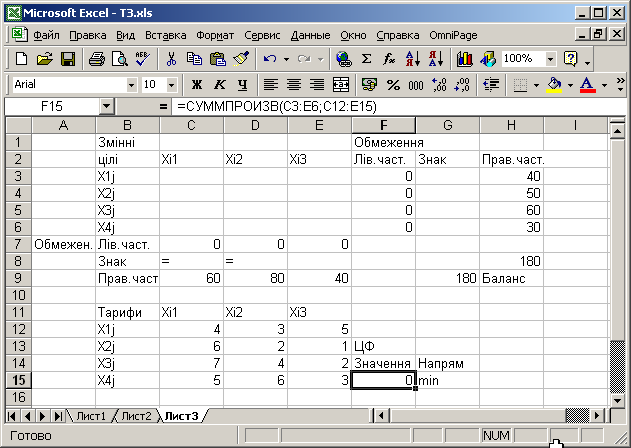
Рис.7.19. Таблиця для введення початкових даних ТЗ
Запишемо формули екранної форми
Об’єкти математичної моделі |
Вираз в Excel |
Змінні задачі |
С3:Е6 |
Формула в цільовій комірці F15 |
=СУММПРОИЗВ(C3:E6;C12:E15) |
Обмеження по рядках в комірках F3, F4, F5, F6 |
=СУММПРОИЗВ(C3:E3) =СУММПРОИЗВ(C4:E4) =СУММПРОИЗВ(C5:E5) =СУММПРОИЗВ(C6:E6) |
Обмеження по стовпцях в комірках C7, D7, E7 |
=СУММПРОИЗВ(C3:C6) =СУММПРОИЗВ(D3:D6) =СУММПРОИЗВ(E3:E6) |
Сумарні запаси і потреби в комірках H8,G9 |
=СУММПРОИЗВ(H3:H6) =СУММПРОИЗВ(C9:F9) |
Наступні дії проводимо в вікні Поиск решения
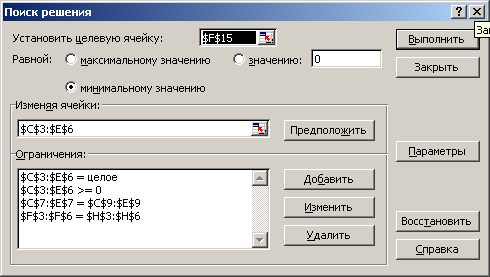 Рис.7.20.
Діалогове вікно Solver
Parameters
Рис.7.20.
Діалогове вікно Solver
Parameters
Розв’язок задачі в екранній формі буде мати вигляд
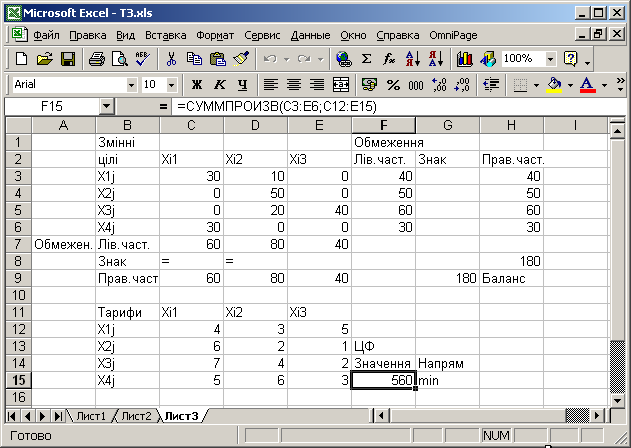
Рис.7.21. Розв’язок ТЗ
