4.6. Теорема Куна-Таккера

В теорії НП центральне місце займає теорема Куна-Таккера. Вона узагальнює класичний метод множників Лагранжа (див. 4.4.) на випадок, коли в задачі НП (4.20)–(4.21) крім обмежень-рівнянь містяться обмеження-нерівності. Тобто, вона встановлює зв'язок між оптимальним планом задачі НП: знайти найбільше значення функції при обмеженнях

,

(4.26)

і сідловою точкою функції Лагранжа для неї

, (4.27)

де

Визначення 4.7. Точка називається сідловою точкою для функції (4.27), якщо -вимірна точка є точкою максимуму функції , а -вимірна точка — точкою мінімуму функції , тобто

. (4.28)

Зауважимо, що запис визначає число, яке дорівнює значенню функції Лагранжа (4.27) в точці , а записи , визначають функції змінних та , які отримують за допомогою функції Лагранжа (4.27) за умови, що зафіксовані лише компоненти векторів та .

Справедлива (доведення опускаємо в силу громіздкості).

Теорема 4.3. (Теорема Куна-Таккера). Нехай існує вектор , для якого виконується (4.28). Тоді необхідною і достатньою умовою оптимальності розв’язку , який належить області допустимих розв'язків, є існування такого вектора , що для всіх і має місце нерівність (4.28).

Таким чином, теорема Куна-Таккера встановлює зв’язок між оптимальним планом задачі (4.20) – (4.21) та сідловою точкою функції Лагранжа (4.27). Тому її називають теоремою про сідлову точку.

Для розв’язку прикладу 4.6, перевіримо виконання умов теореми Куна-Таккера. Запишемо функцію Лагранжа

.

Підставивши ( , тому, що відповідне обмеження не є визначальним) у функцію Лагранжа, отримаємо

, ,

.

Ліва нерівність в (4.28) виконується як рівність, а права запишеться так: . Оскільки значення цільової функції в області допустимих розв’язків не менше свого мінімального значення , а другий доданок (з другого обмеження прикладу 4.6 випливає ) невід’ємний, то остання нерівність виконується.

Якщо функції і , , диференційовані, то нерівності (4.28) та , еквівалентні так званим локальним умовам Куна-Таккера в точці :

(4.29)

(4.30)

, (4.31)

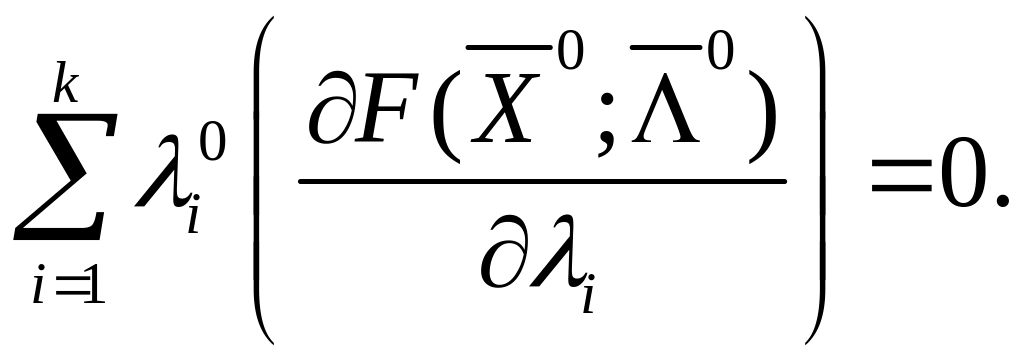(4.32)

Контрольні запитання та задачі

1. Дайте визначення функції багатьох змінних, границі функції багатьох змінних, частинної похідної.

2. Яку функцію називають неперервною в точці?

3. Дайте визначення локального та глобального екстремумів, квадратичної форми, додатно (від’ємно) визначеної квадратичної форми.

4. Сформулюйте критерій Сильвестра додатної (від’ємної) визначеності квадратичної форми.

5. В якому випадку точка є точкою локального екстремуму?

6. Дайте визначення умовного екстремуму.

7. Які методи використовують при розв’язуванні задач на умовний екстремум?

8. Як формулюється ЗНП в загальному вигляді?

9. На які види діляться ЗНП?

10. Які задачі відносяться до задач ДЛП?

11. Наведіть алгоритм розв’язування ЗНП методом множників Лагранжа.

12. Дайте економічну інтерпретацію множників Лагранжа.

13. Сформулюйте алгоритм графічного методу розв’язування ЗНП.

14. Яка точка називається сідловою?

15. Сформулюйте теорему Куна-Таккера.

16. Знайти найменше значення цільової функції 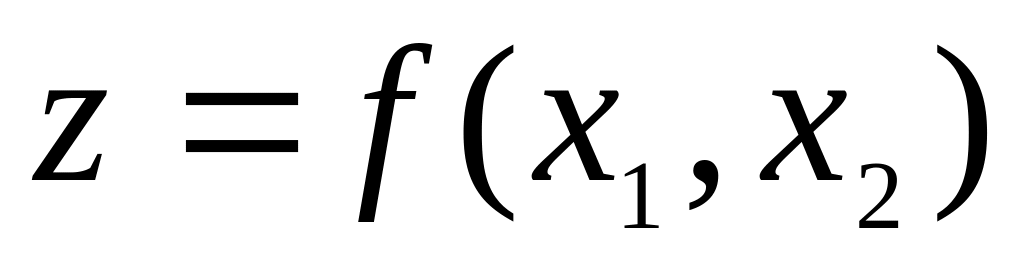при заданих обмеженнях; перевірити виконання умов Куна-Таккера.

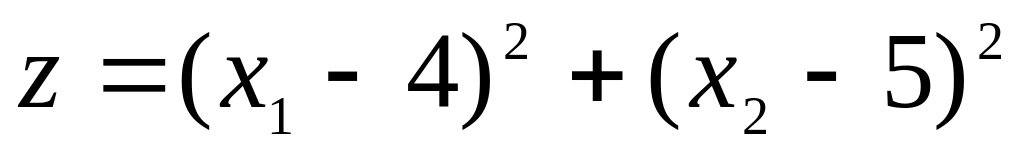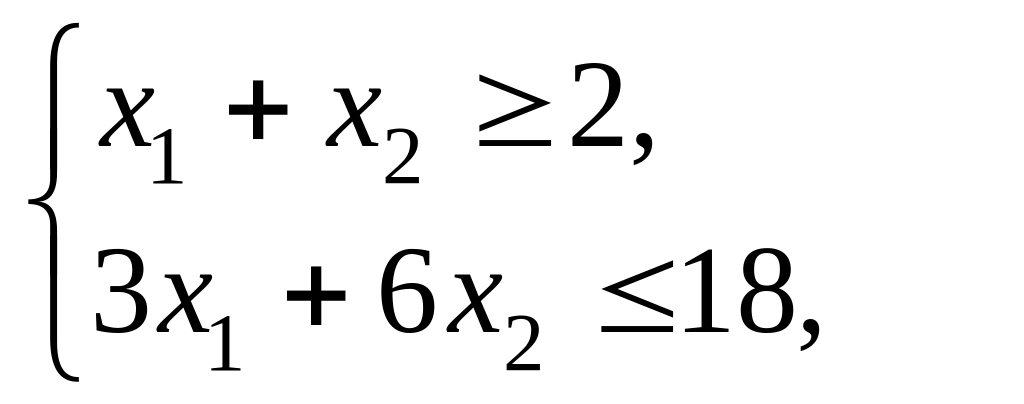
    а) ,	б) 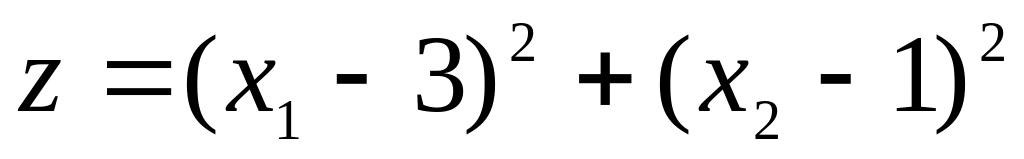,	в)
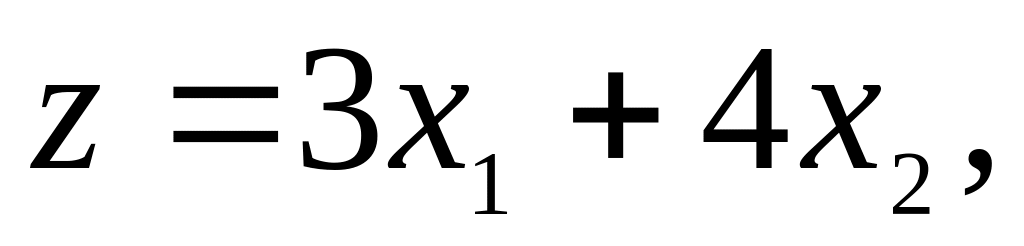
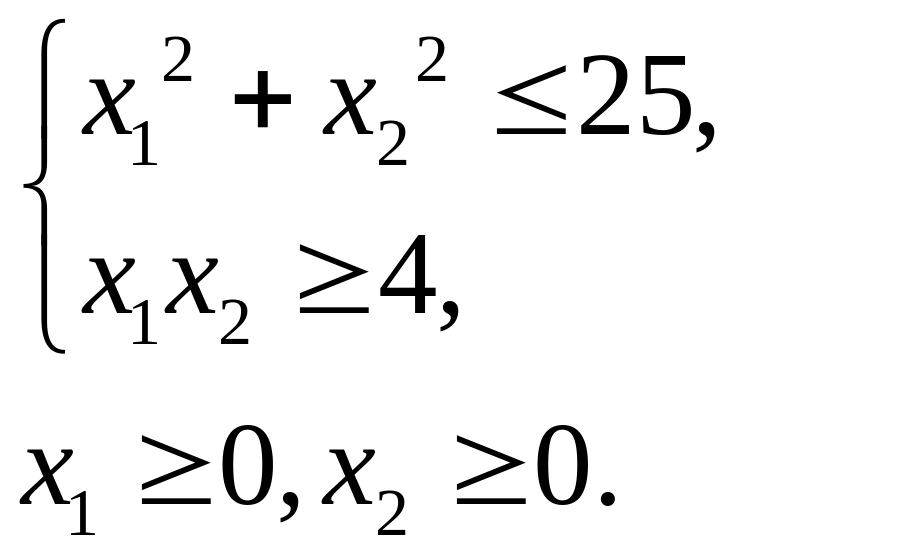
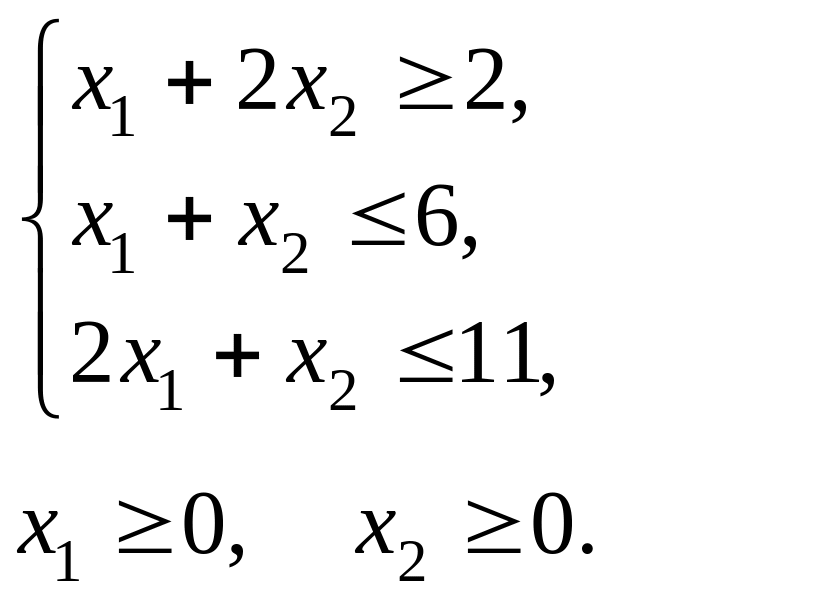
    г) ,	д)

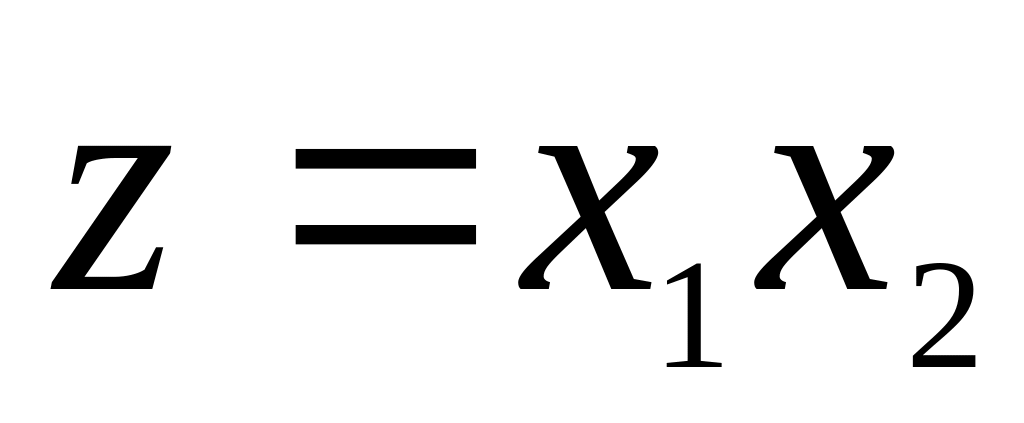
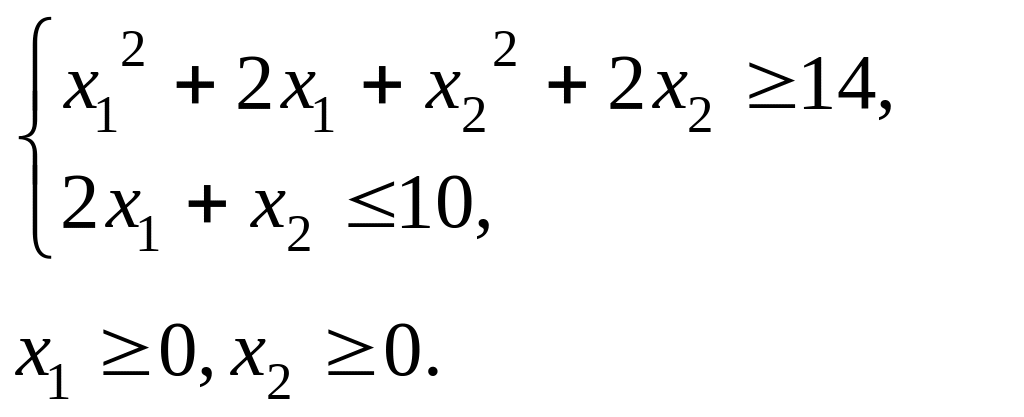
17. Методом множників Лагранжа визначити стаціонарні точки функції 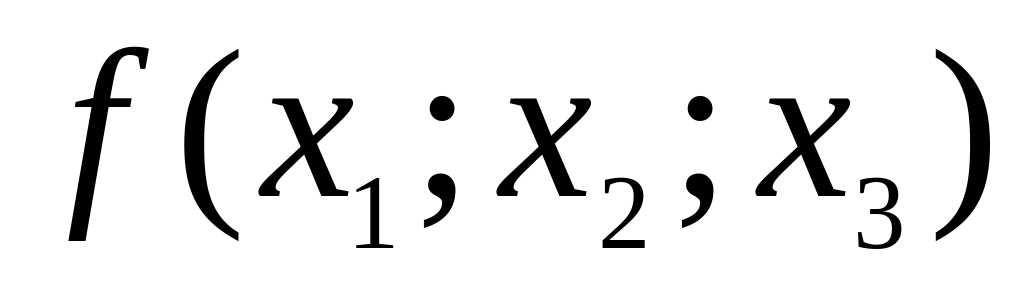при обмеженнях:

а)

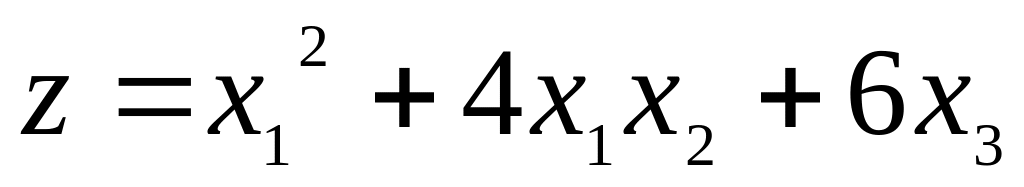
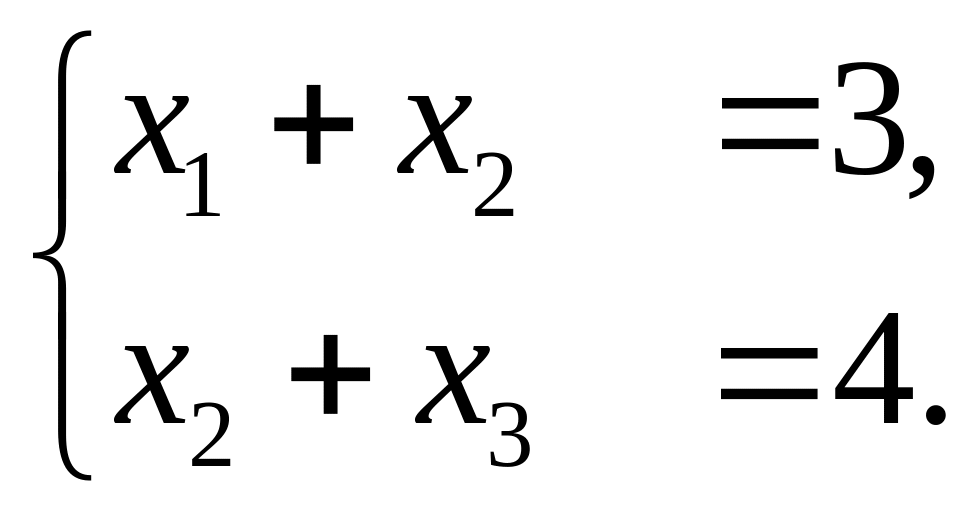
б)

18. Знайти умовний екстремум функції 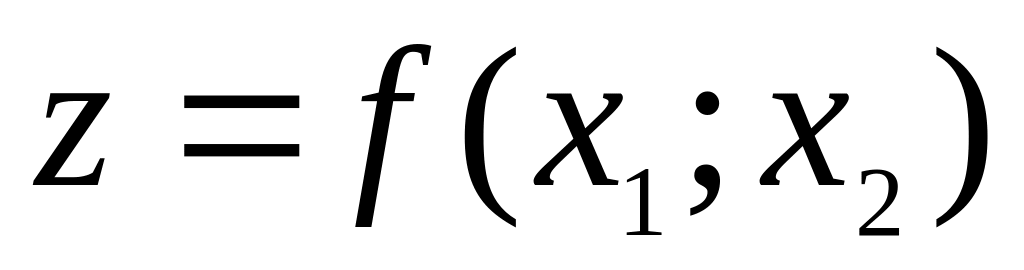за умови:

а) ,

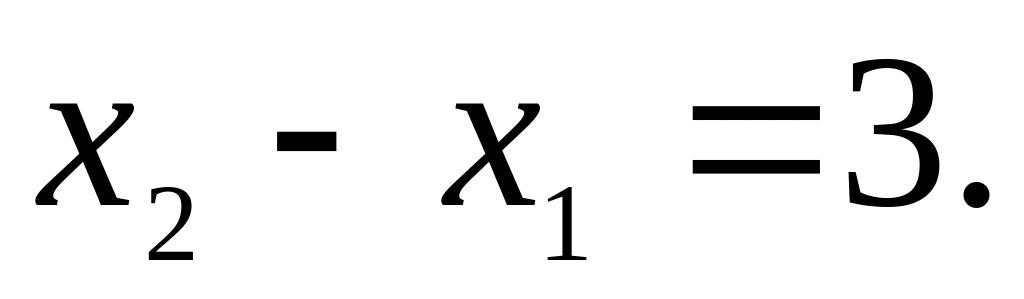
б) ,

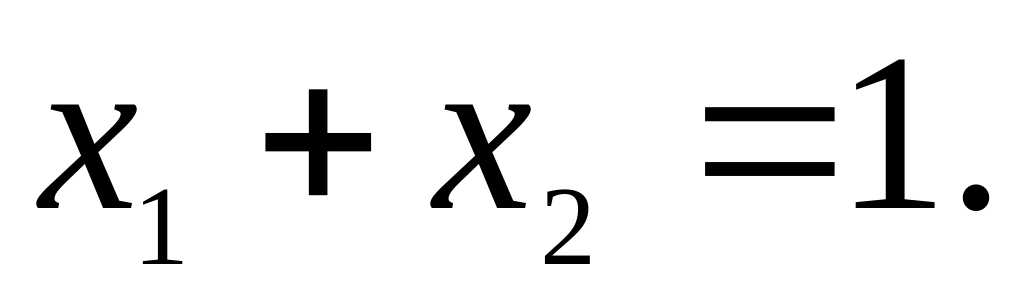
19. Знайти найбільше значення функції :

а)

б)

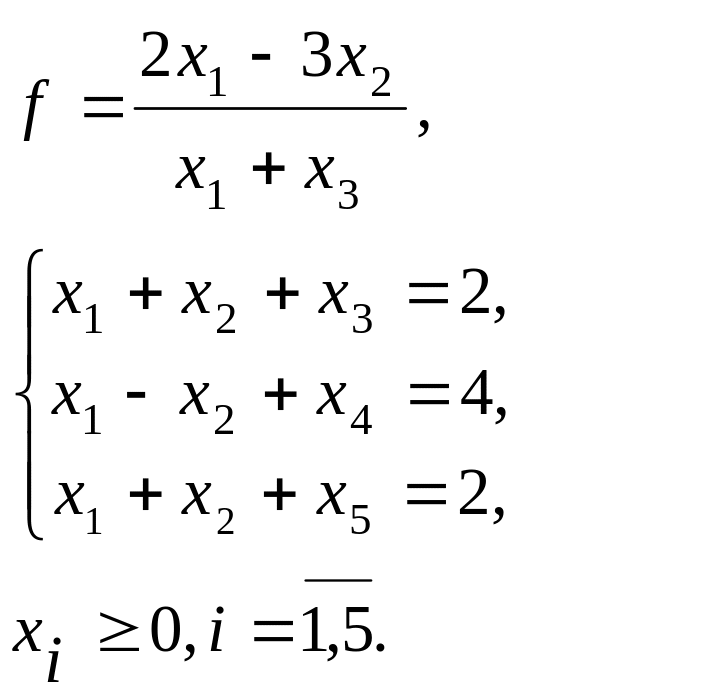
4. Знайти найменше значення функції

а)

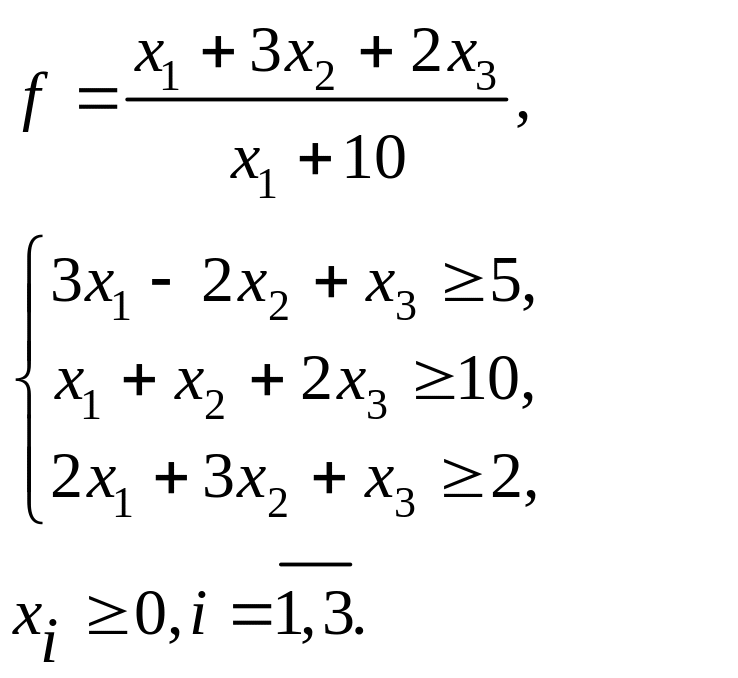
б)

РОЗДІЛ 5. ДИНАМІЧНЕ ПРОГРАМУВАННЯ (ДП)