2.Навчальний матеріал.

Тема: Повторення і розширення відомостей про функції.

1.Означення функції.Зростаючі, спадні, парні і непарні функції.

Матеріальна єдність світу виявляється у взаємозв'язку і взаємообумовленості різних явищ і процесів, що відбуваються у природі.Розглядаючи їх, доводиться враховувати залежності одних змінних величин від інших.

Наприклад, залежність шляху від часу, залежність між площею круга і його радіусом.Необхідність вивчення на практиці залежностей між змінними різної природи привела до поняття функції в математиці.

Залежність змінної у від змінної х називається функцією, якщо кожному значенню х відповідає єдине значення у. Функцію позначають у =f(х), яка символічно означає залежність між двома змінними. Змінну х називають незалежною

або аргументом, а змінну у – залежною.

Множина значень,яких набуває незалежна зміння х , називається областю визначення функції. Множина відповідних значень залежної змінної у, яких вона набуває при всіх значеннях х з області визначення функції, називається областю значень, або областю зміни функції.

Приклад 1. Залежність шляху s тіла, яке рухається рівномірно, від часу t

є функцією, що задається формулою s = s_o + vt ,де s_o - початковий шлях, v - швидкість, яка є сталою при рівномірному русі.

Приклад 2.Якщо студенти групи, яка складається з 25 осіб чергують протягом січня, крім тих днів, які припадають на неділлю, то кожному з днів січня відповідає певний черговий. Незалежною змінною тут є дні січня, залежною – черговий. Маємо функцію, областю визначення якої є множина днів січня (без неділь), а областю зміни – множина студентів групи.

Приклад 3.Активна електрична енергія, яка витрачається в колі змінного струму за час t, є функцією часу при сталій потужності P виражається формулою W_a =Pt.

Означення: числовою функцією з областю визначення х називається залежність, при якій кожному числовому значенню х з множини Х ставиться у відповідність єдине деяке число у.

Основні способи задання функції:

1. за допомогою формули;

2. за допомогою таблиці (наприклад,таблиці квадратів чисел, значень тригонометричних функцій та ін.);

3. за допомогою графіка.

11

Графіком функції y = f(x) називається множина точок M(x; f(x)) координатної площини, абсциси яких належать області визначення функції, а ординати є відповідними значеннями цієї функції.

Не завжди формула задає функцію.наприклад, формуло I = U/R (закон Ома)

Задає пряму пропорційність (функцію від U) при сталому опорі в колі і змінній напрузі і задає обернену пропорційність (функцію від R) при сталій напрузі і змінному опорі. Проте, якщо з цієї формули виразити R, то R = U/R. Остання формула не задає функцію.Справді, R – величина стала для даного провідника і не залежить ні від напруги ні від сили струму.Якщо напругу збільшити, наприклад, у 2 рази, то в 2 рази збільшиться і сила струму, а відношення напруги до сили струму не зміниться.

Опір R є функцією (прямою пропорційністю у = kx) довжини провідника при сталій площі поперечного перерізу і функцією площі поперечного перерізу

(оберненою пропорційністю у = k/x) при сталій довжині провідника R= ρ·l/S, де

ρ – питомий опір; l – довжина провідника; S – площа його поперечного перерізу.

Інколи функцію задають різними формулами на різних множинах значень аргументу. Наприклад, якщо турист був у дорозі 9 год і перші 5 год рухався зі швидкістю 4,5 км/год, потім відпочивав 0,5 год, а решту часу йшов зі швидкістю

4 км/год, то функцію шляху s залежно від часу t запишемо у вигляді

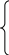
4,5t, якщо 0 < t ≤ 5,

s = 22,5, якщо 5 < t ≤ 5,5,

22,5 + 4(t – 5,5), якщо 5,5 < t ≤ 9

Функція y = f(x) називається зростаючою, якщо більшому значенню аргументу відповідає більше значення функції, тобто для будь-яких двох значень х₁ та х₂ змінної ч, взятих з області визначення , і таких, що х₂ > х₁ , справджується нерівність f₂(x) > f₁(x).

Функція у = f(x) називається спадною, якщо більшому значенню аргумента відповідає менше значення функції, тобто для будь-яких двох значень

х₁ , х₂ зміної х взятих з області визначення, і таких, що х₁ > х₂ , справджується нерівність f(x₂) < f(x₁)/

Для дослідження функцій на зростання і спадання, виходячи з їх означень, треба:

1)вибрати будь-які два значення х₁ і х₂ з області визначення функції такі, що х₂>х₁ ;

2)скласти різницю f(x) – f(x) і з'ясувати (якщо це можливо), чи буде вона додатною (від'ємною) і, користуючись означенням нерівності, переконатися, що f(x₂)>f(x₁)(чи f(x₂) <f(x₁)),а звідси зробити висновок, про зростання (спадання) функції. У зростаючої функції графік піднімається вгору, у спадної – опускається вниз.

12

Функція y =f(x) називається парною, якщо для будь-якого значення х в області визначення значення (-х) також належить області визначення і справджується рівність f(-x) =f(x). У парних функцій їх значення для протилежних значень аргументу рівні. Графік парної функції симетричний відносно осі Оу.

Функція y =f(x) називається непарною, якщо для будь-якого значення х з області визначення значення (-х) також належить області визначення і справджується рівність f(-x) = -f(x) .У непарних функцій їх значення для протилежних значень аргументу протилежні. Графік непарної функції симетричний відносно початку координат..

Приклади. 1 Функція у = 2х зростаюча і непарна у всій області визначення.Графік її симетричний відносно початку координат.

2)Функція у =х² зростаюча при х є [0 ; +∞) і спадною при х хє(-∞;0].

Вона парна, її графік симетричний відносно Оу.Щоб дослідити функцію на парність чи непарність, треба:

1)перевірити виконання умови: для будь-якого х з області визначення (-х) також належить області визначення, тобто перевірити, чи буде область даної функції множиною, симетричною відносно точки 0;

2)перевірити виконання умови: f(-x) = f (x) чи f(-x) = - f(x).

Якщо не виконується перша умова, то немає сенсу перевіряти другу.

13